学习笔记·不等式

不等式的基本性质

研究不等式的出发点是实数的大小关系。不等式的基础建立在以下两条公理之上：
公理1：对于任意实数\(a\)，\(a = 0\)、\(a\)为正数、\(a\)为负数这三者有且只有一个成立。
公理2：对于任意正数\(a, b\)，\(a + b, ab\)都是正数。

由这两条公理可以得到推论：
对于任意正数\(a\)和负数\(b\)，\(ab\)是负数；对于任意负数\(a, b\)，\(a + b\)是负数，\(ab\)是正数。

如果\(a - b\)是正数，那么称\(a\)大于（greater than）\(b\)，记作\(a > b\)；如果\(a - b\)是负数，那么称\(a\)小于（less than）\(b\)，记作\(a < b\)。这两种不等关系都属于严格不等（strict inequalities）。
另外，如果\(a > b\)或\(a = b\)，那么称\(a\)大于等于（greater than or equal to）\(b\)，记作\(a \ge b\)；如果\(a < b\)或\(a = b\)，那么称\(a\)小于等于（less than or equal to）\(b\)，记作\(a \le b\)。

实际上，令\(b = 0\)，那么\(a > 0\)就表示\(a\)是正数，\(a < 0\)就表示\(a\)是负数。

根据公理1，可以得到不等式的三歧性：
\(a > b, a < b, a = b\)这三者有且只有一个成立。

不等式的对称性： \[a > b \Leftrightarrow b < a, a < b \Leftrightarrow b > a\]

不等式的传递性： \[ \begin{align} & a > b, b > c \Rightarrow a > c \\ & a < b, b < c \Rightarrow a < c \end{align} \]

此外，在运算中，不等式也有一些性质：
若\(a > b, c \ge d\)，则\(a + c > b + d\)。

由这条显然可以得到推论：
若\(a > b\)，则\(a + c > b + c\)。

关于乘法有：
若\(a > b, c > 0\)，则\(ac > bc\)；如果\(c < 0\)，则\(ac < bc\)。

同样有推论：
若\(a > b > 0, c > d > 0\)，则\(ac > bd\)。

此外有：
若\(a > b > 0\)，\(n\)为正整数，则\(a^{n} > b^{n}\)。

若\(a > b > 0\)，则\(\dfrac{1}{a} < \dfrac{1}{b}\)。

若\(a > b > 0\)，\(n\)为正整数，则\(a^{\frac{1}{n}} > b^{\frac{1}{n}}\)。
这条证明如下：
设\(c = a^{\frac{1}{n}}, d = b^{\frac{1}{n}}\)，则\(a = c^{n}, b = d^{n}\)。此时\(a - b = c^{n} - d^{n} = (c - d) (c^{n - 1} + c^{n - 2} d + \cdots + d^{n - 1})\)。由\(n\)次方根定义，\(c, d\)为正数，故\(c^{n - 1} + c^{n - 2} d + \cdots + d^{n - 1}\)为正数，可得\(c - d\)为正数。\(\Box\)

最后这一条定理是大多数不等式证明的基础：
对于任意实数\(a\)，\(a^{2} \ge 0\)，等号成立当且仅当\(a = 0\)。

糖水不等式有：（\(0 < a < b, c > 0\)） \[\dfrac{a}{b} < \dfrac{a + c}{b + c}\]

往糖水里加糖会变得更甜，这就是糖水不等式的直观体现。其证明可以就从定义出发： \[\dfrac{a + c}{b + c} - \dfrac{a}{b} = \dfrac{b (a + c) - a (b + c)}{b (b + c)} = \dfrac{c (b - a)}{b (b + c)}\] 由\(0 < a < b, c > 0\)，得\(\dfrac{c (b - a)}{b (b + c)} > 0\)，不等式成立。\(\Box\)

简单不等式的求解

一元一次不等式

一元一次不等式是最简单的不等式，其基本形式为\(ax > b\)。
如果\(a > 0\)，那么解集为\(x > \dfrac{b}{a}\)；
如果\(a < 0\)，那么解集为\(x < \dfrac{b}{a}\)；
如果\(a = 0\)，且\(b < 0\)，那么解集为\(\mathbb{R}\)，若\(b \ge 0\)，解集为\(\varnothing\)。

一元二次不等式

设二次函数\(f(x) = ax^{2} + bx + c (a > 0)\)，令\(\Delta = b^{2} - 4ac\)。由函数图像可以直观地得到：
如果\(\Delta > 0\)，设\(f(x) = 0\)的两根\(x_{1} < x_{2}\)，那么\(f(x) > 0\)的解集为\(x > x_{2}\)或\(x < x_{1}\)，\(f(x) < 0\)的解集为\(x_{1} < x < x_{2}\)；
如果\(\Delta = 0\)，那么\(f(x) = 0\)有唯一根\(x_{0} = -\dfrac{b}{2a}\)，\(f(x) \ge 0\)恒成立，此时\(f(x) > 0\)的解集为\(x \ne x_{0}\)，\(f(x) < 0\)的解集为\(\varnothing\)；
如果\(\Delta < 0\)，那么\(f(x) > 0\)恒成立，解集为\(\mathbb{R}\)，\(f(x) < 0\)的解集为\(\varnothing\)。

一元\(n\)次不等式

一元\(n\)次不等式是形如\(f(x) = a_{0} x^{n} + a_{1} x^{n - 1} + \cdots + a_{n} > 0 (a_{0} \ne 0)\)的不等式。从虚根成对定理的证明中，我们知道任何\(n\)次实系数多项式\(f(x)\)都可以在实数范围内分解为 \[f(x) = a \prod_{k=1}^{s} (x - a_{k}) \cdot \prod_{k=1}^{t} (x^{2} + b_{k} x + c_{k})\]

其中\(s + 2t = n\)。由于二次因式都没有实根，恒大于零，因此我们只要解不等式 \[(x - x_{1}) (x - x_{2}) \cdots (x - x_{s}) > 0\]

其中可能会有重根，因此又可以写成 \[(x - a_{1})^{n_{1}} (x - a_{2})^{n_{2}} \cdots (x - a_{k})^{n_{k}} > 0 (n_{1}, \cdots, n_{k} \in \mathbb{N}^{\ast})\]

通常我们用穿针引线法来解这类不等式：

1. 画一个数轴，数轴上方表示\(f(x) > 0\)，下方表示\(f(x) < 0\)，在数轴上表示出\(a_{1}, \cdots, a_{k} (a_{1} > \cdots > a_{k})\)；
2. 从\(a_{1}\)的右上方开始画向左下的曲线，若指数\(n_{1}\)是奇数，则曲线穿过数轴继续向下，否则曲线折返向上；
3. 在\(a_{2}, \cdots, a_{k}\)处重复和\(a_{1}\)一样的操作；
4. \(f(x) > 0\)的解集为最后图像的数轴上方的部分，\(f(x) < 0\)的解集为数轴下方的部分，如果有等号就并上零点。

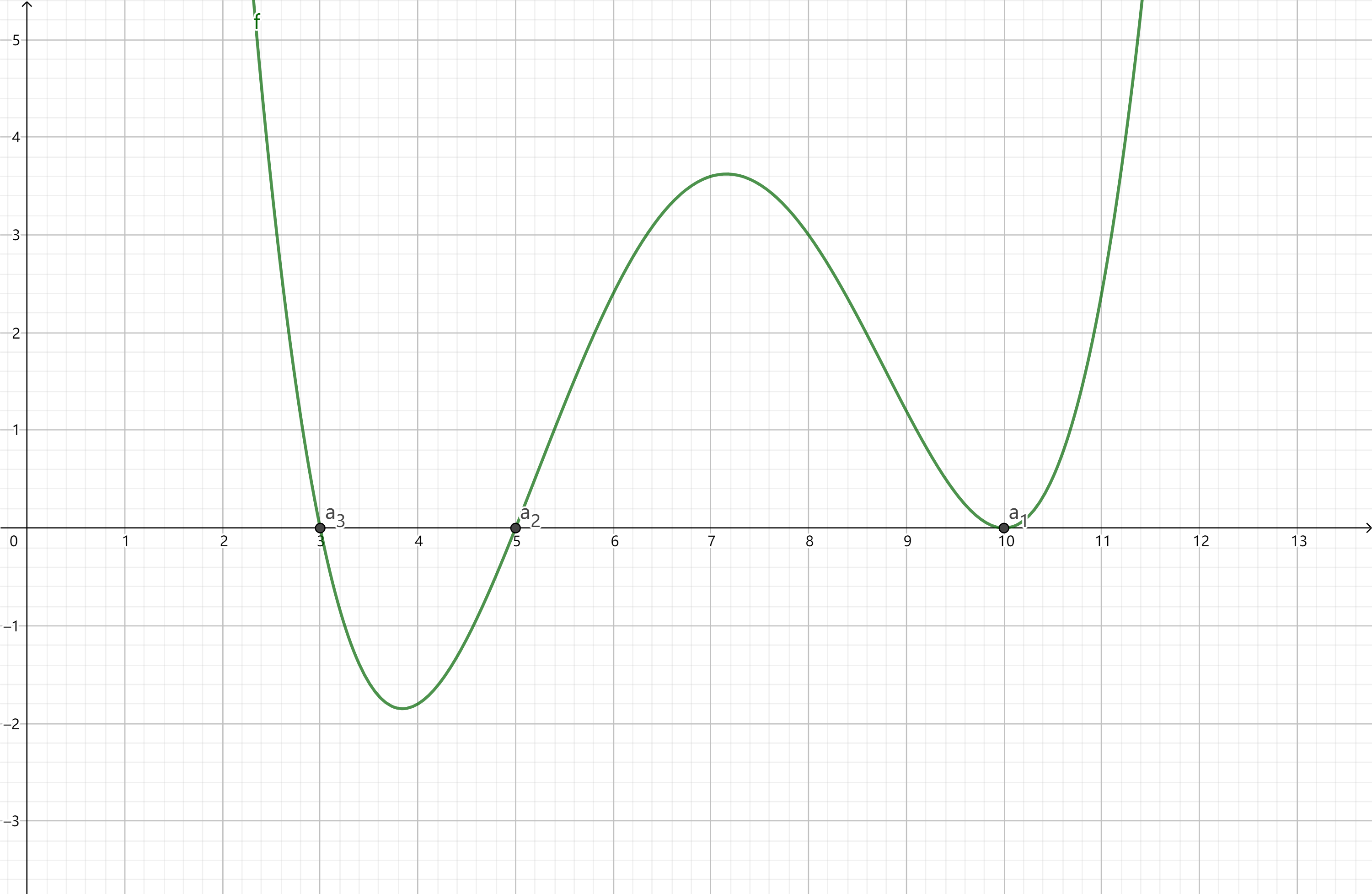
例如，对于上图，不等式\(f(x) > 0\)的解集为\((-\infty, a_{3}) \cup (a_{2}, a_{1}) \cup (a_{1}, +\infty)\)；不等式\(f(x) < 0\)的解集为\((a_{3}, a_{2})\)。

分式不等式

形如\(\dfrac{f(x)}{g(x)} > 0\)的分式不等式，总是可以化为以下形式： \[ \begin{align} & \dfrac{f(x)}{g(x)} > 0 \Leftrightarrow \begin{cases} f(x) > 0 \\ g(x) > 0 \end{cases} \ \mathrm{or} \ \begin{cases} f(x) < 0 \\ g(x) < 0 \end{cases} \\ & \dfrac{f(x)}{g(x)} \ge 0 \Leftrightarrow \begin{cases} f(x) \ge 0 \\ g(x) > 0 \end{cases} \ \mathrm{or} \ \begin{cases} f(x) \le 0 \\ g(x) < 0 \end{cases} \\ & \dfrac{f(x)}{g(x)} < 0 \Leftrightarrow \begin{cases} f(x) > 0 \\ g(x) < 0 \end{cases} \ \mathrm{or} \ \begin{cases} f(x) < 0 \\ g(x) > 0 \end{cases} \\ & \dfrac{f(x)}{g(x)} \le 0 \Leftrightarrow \begin{cases} f(x) \ge 0 \\ g(x) < 0 \end{cases} \ \mathrm{or} \ \begin{cases} f(x) \le 0 \\ g(x) > 0 \end{cases} \end{align} \]

此外，我们发现： \[f^{2}(x) = f(x) g(x) \cdot \dfrac{f(x)}{g(x)} \ge 0\]

那么， \[\dfrac{f(x)}{g(x)} > 0 \Leftrightarrow f(x) g(x) > 0\]

不过，由于分母不能为零，所以 \[\dfrac{f(x)}{g(x)} \ge 0 \Leftrightarrow \begin{cases} f(x) g(x) \ge 0 \\ g(x) \ne 0 \end{cases}\]

平均值不等式与柯西不等式

算术-几何平均值不等式

我们知道，\((a \pm b)^{2} \ge 0\)，很容易有推论\(a^{2} + b^{2} \ge 2|ab|\)。
由此得到基本不等式：
对于任意非负实数\(a, b\)，\(\dfrac{a + b}{2} \ge \sqrt{ab}\)，等号成立当且仅当\(a = b\)。

\(\dfrac{a + b}{2}\)称为\(a, b\)的算术平均数（arithmetic mean），\(\sqrt{ab}\)称为\(a, b\)的几何平均数（geometric mean），因此，这个不等式也叫二元算术-几何平均值不等式，简称二元平均值不等式。

基本不等式有一些简单推论：
对于任意非负实数\(a, b\)，\(a + b \ge 2 \sqrt{ab}\)；
对于任意非负实数\(a, b\)，\(ab \le \left(\dfrac{a + b}{2} \right)^{2}\)。

此外，用基本不等式可以立刻得到对勾函数\(f(x) = x + \dfrac{a}{x} (a > 0)\)的值域。
\(x > 0\)时，\(f(x) = x + \dfrac{a}{x} \ge 2 \sqrt{x \cdot \dfrac{a}{x}} = 2 \sqrt{a}\)，等号成立当且仅当\(x = \dfrac{a}{x}\)即\(x = \sqrt{a}\)。那么由函数奇偶性，得到值域为\((-\infty, 2 \sqrt{a}] \cup [2 \sqrt{a}, +\infty)\)。

三元算术-几何平均值不等式：
对于任意非负实数\(a, b, c\)，\(\dfrac{a + b + c}{3} \ge \sqrt[3]{abc}\)，等号成立当且仅当\(a = b = c\)。

证明： \[ \begin{align} x^{3} + y^{3} + z^{3} - 3xyz &= (x + y + z) (x^{2} + y_{2} + z^{2} - xy - yz - zx) \\ &= \dfrac{1}{2} (x + y + z) \left((x - y)^{2} + (y - z)^{2} + (z - x)^{2} \right) \ge 0 \end{align} \] 得到\(x^{3} + y^{3} + z^{3} \ge 3xyz\)。令\(x = \sqrt[3]{a}, y = \sqrt[3]{b}, z = \sqrt[3]{c}\)即可。\(\Box\)

同样有推论：
对于任意非负实数\(a, b, c\)，\(abc \le \dfrac{a^{3} + b^{3} + c^{3}}{3}\)；
对于任意非负实数\(a, b, c\)，\(abc \le \left(\dfrac{a + b + c}{3} \right)\)。

再推广一些，可以得到一般的算术-几何平均值不等式（AM–GM inequality），可以简称平均值不等式：
设\(n\)是正整数，对于非负实数\(a_{1}, \cdots, a_{n}\)， \[\dfrac{a_{1} + \cdots + a_{n}}{n} \ge \sqrt[n]{a_{1} \cdots a_{n}}\] 等号成立当且仅当\(a_{1} = \cdots = a_{n}\)。

除了数学归纳法，我们也可以使用调整法来证明：
设\(A = \dfrac{a_{1} + \cdots + a_{n}}{n}\)。如果\(a_{1} = \cdots = a_{n} = A\)，那么\(\sqrt[n]{a_{1} \cdots a_{n}} = A\)。否则，设\(f(x_{1}, \cdots, x_{n}) = \sqrt[n]{x_{1} \cdots x_{n}}\)，要证明的就是\(f(a_{1}, \cdots, a_{n}) \le A\)。
如果存在\(a_{i} < A\)，那么必有\(a_{j} > A\)。设\(a_{1} > A > a_{2}\)，令\(\delta = \min(a_{1} - A, A - a_{2})\)，\(a_{1}' = a_{1} - \delta, a_{2}' = a_{2} + \delta, a_{k}' = a_{k} (3 \le k \le n)\)，则\(\dfrac{a_{1}' + \cdots + a_{n}'}{n} = A\)也成立。因为\(0 < \delta < a_{1} - a_{2}\)，有\(a_{1}' a_{2}' = (a_{1} - \delta) (a_{2} + \delta) = a_{1} a_{2} + \delta (a_{1} - a_{2} - \delta) > a_{1} a_{2}\)，从而有\(f(a_{1}, \cdots, a_{n}) < f(a_{1}', \cdots, a_{n}')\)。
这样的操作进行至多\(n\)次，便可让所有数都变为\(A\)，最后得到\(f(a_{1}, \cdots, a_{n}) < f(a_{1}', \cdots, a_{n}') < \cdots < A\)。\(\Box\)

柯西不等式

对于任意\(n\)维向量\(\mathbf{a}, \mathbf{b}\)，其夹角 \[\langle \mathbf{a}, \mathbf{b} \rangle = \dfrac{|\mathbf{a} \cdot \mathbf{b}|}{|\mathbf{a}| |\mathbf{b}|} \le 1\]

因而有\(|\mathbf{a} \cdot \mathbf{b}| \le |\mathbf{a}| |\mathbf{b}|\)。令\(\mathbf{a} = (a_{1}, \cdots, a_{n}), \mathbf{b} = (b_{1}, \cdots, b_{n})\)，平方可得 \[(a_{1} b_{1} + \cdots + a_{n} b_{n})^{2} \le (a_{1}^{2} + \cdots + a_{n}^{2}) (b_{1}^{2} + \cdots + b_{n}^{2})\]

就得到柯西不等式（Cauchy’s inequality）：
对于两组非负实数\(a_{1}, \cdots, a_{n}\)和\(b_{1}, \cdots, b_{n}\)， \[\left(\sum\limits_{i=1}^{n} a_{i} b_{i} \right)^{2} \le \left(\sum\limits_{i=1}^{n} a_{i}^{2} \right) \left(\sum\limits_{i=1}^{n} b_{i}^{2} \right)\] 等号成立当且仅当\(\dfrac{a_{1}}{b_{1}} = \cdots = \dfrac{a_{n}}{b_{n}}\)。

代数证明如下：
如果\(a_{i}\)全为零，不等式显然成立。否则，令二次函数\(f(x) = \sum\limits_{i=1}^{n} (a_{i} x + b_{i})^{2}\)，展开为 \[f(x) = \left(\sum\limits_{i=1}^{n} a_{i}^{2} \right) x^{2} + 2 \left(\sum\limits_{i=1}^{n} a_{i} b_{i} \right) x + \sum\limits_{i=1}^{n} b_{i}^{2}\] 由于函数值恒不小于零， \[\Delta = \left(2 \sum\limits_{i=1}^{n} a_{i} b_{i} \right)^{2} - 4 \left(\sum\limits_{i=1}^{n} a_{i}^{2} \right) \left(\sum\limits_{i=1}^{n} b_{i}^{2} \right) \le 0\] 得到结果。\(\Box\)

调和-几何-算术-平方平均值不等式（HM-GM-AM-QM inequalities）： 对于正数\(a_{1}, \cdots, a_{n}\)， \[\dfrac{n}{a_{1}^{-1} + \cdots + a_{n}^{-1}} \le \sqrt[n]{a_{1} \cdots a_{n}} \le \dfrac{a_{1} + \cdots + a_{n}}{n} \le \sqrt{\dfrac{a_{1}^{2} + \cdots + a_{n}^{2}}{n}}\] 等号成立当且仅当\(a_{1} = \cdots = a_{n}\)。

从左到右依次证明：
第一个不等式：由算术-几何平均值不等式，\(a_{1}^{-1} + \cdots + a_{n}^{-1} \ge n \sqrt[n]{a_{1}^{-1} \cdots a_{n}^{-1}} = \dfrac{n}{\sqrt[n]{a_{1} \cdots a_{n}}}\)；
第二个不等式：即算术-几何平均值不等式；
第三个不等式：由柯西不等式，\(n (a_{1}^{2} + \cdots + a_{n}^{2}) = (a_{1}^{2} + \cdots + a_{n}^{2}) (1 + \cdots + 1) \ge (a_{1} + \cdots + a_{n})^{2}\)，即\(a_{1} + \cdots + a_{n} \le \sqrt{n (a_{1}^{2} + \cdots + a_{n}^{2})}\)。\(\Box\)

其中，\(\dfrac{n}{a_{1}^{-1} + \cdots + a_{n}^{-1}}\)称为调和平均数（harmonic mean），\(\sqrt{\dfrac{a_{1}^{2} + \cdots + a_{n}^{2}}{n}}\)称为平方平均数（quadratic mean）。

不等式证明的基本方法

比较法

比较法是证明不等式的最朴素的方法。通常把要证的不等式两边相减，变形为一个容易证明的不等式。

例如，证明切比雪夫不等式（Chebyshev’s inequality）：
对于实数\(a_{1} < \cdots < a_{n}, b_{1} < \cdots < b_{n}\)， \[n \sum\limits_{i=1}^{n} a_{i} b_{i} > \left(\sum\limits_{i=1}^{n} a_{i} \right) \left(\sum\limits_{i=1}^{n} b_{i} \right)\]

左边减去右边，得 \[ \begin{align} n \sum\limits_{i=1}^{n} a_{i} b_{i} - \left(\sum\limits_{i=1}^{n} a_{i} \right) \left(\sum\limits_{i=1}^{n} b_{i} \right) &= n \sum\limits_{i=1}^{n} a_{i} b_{i} - \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} a_{i} b_{j} \\ &= (n - 1) \sum\limits_{i=1}^{n} a_{i} b_{i} - \dfrac{1}{2} \sum\limits_{i \ne j} (a_{i} b_{j} + a_{j} b_{i}) \\ &= \dfrac{1}{2} \sum\limits_{i \ne j} (a_{i} b_{i} + a_{j} b_{j}) - \dfrac{1}{2} \sum\limits_{i \ne j} (a_{i} b_{j} + a_{j} b_{i}) \\ &= \dfrac{1}{2} \sum\limits_{i \ne j} (a_{i} b_{i} + a_{j} b_{j} - a_{i} b_{j} - a_{j} b_{i}) \\ &= \dfrac{1}{2} \sum\limits_{i \ne j} (a_{i} - a_{j}) (b_{i} - b_{j}) \end{align} \] 根据条件，\(i > j\)时\(a_{i} > a_{j}, b_{i} > b_{j}\)，\((a_{i} - a_{j}) (b_{i} - b_{j}) > 0\)。同理，\(i < j\)时\((a_{i} - a_{j}) (b_{i} - b_{j}) > 0\)。所以两式相减大于零。\(\Box\)

分析法

分析法是从要证的不等式出发进行等价变形，直到式子可以证明。

例如，设\(a, b, c\)为三角形的三条边，求证：
对于任意正数\(m\)都有 \[\dfrac{a}{a + m} + \dfrac{b}{b + m} > \dfrac{c}{c + m}\]

证明这个不等式就是要证\(\dfrac{2ab + m (a + b)}{ab + m (a + b) + m^{2}} > \dfrac{c}{c + m}\)，也就是\(\dfrac{ab + m (a + b) + m^{2}}{2ab + m (a + b)} < \dfrac{c + m}{c}\)。因为\(\dfrac{ab + m (a + b) + m^{2}}{2ab + m (a + b)} = 1 + \dfrac{m^{2} - ab}{2ab + m (a + b)}, \dfrac{c + m}{c} = 1 + \dfrac{m}{c}\)，所以只要证明\(\dfrac{m^{2} - ab}{2ab + m (a + b)} < \dfrac{m}{c}\)，也就是\(c (m^{2} - ab) < m (2ab + m (a + b))\)，即\(m^{2} (a + b - c) \ge -ab (2m + c)\)。因为\(a, b, c\)为三角形的三条边，所以\(a + b - c > 0\)，从而左边为正，右边为负。\(\Box\)

放缩法

若要证明\(A \le B\)，可以找到容易证明的\(A \le C\)和\(C \le B\)，这就是“放”；找到\(B \ge D\)和\(D \ge A\)，这就是“缩”。合称放缩法。

例如，设\(0 < a \le b \le c \le \dfrac{1}{2}\)，求证： \[\dfrac{1}{a (1 - b)} + \dfrac{1}{b (1 - a)} \ge \dfrac{2}{c (1 - c)}\]

设函数\(f(x) = x (1 - x)\)，容易证明\(f\)在\([0, \dfrac{1}{2}]\)上是增函数，所以\(a (1 - a) \le b (1 - b) \le c (1 - c)\)。从而得到\(\dfrac{2}{c (1 - c)} \le \dfrac{1}{a (1 - a)} + \dfrac{1}{b (1 - b)}\)，那么就只要证明\(\dfrac{1}{a (1 - b)} + \dfrac{1}{b (1 - a)} \ge \dfrac{1}{a (1 - a)} + \dfrac{1}{b (1 - b)}\)。 \[ \begin{align} \dfrac{1}{a (1 - b)} + \dfrac{1}{b (1 - a)} - \dfrac{1}{a (1 - a)} - \dfrac{1}{b (1 - b)} &= \dfrac{b (1 - a) + a (1 - b) - b (1 - b) - a (1 - a)}{ab (1 - a) (1 - b)} \\ &= \dfrac{a^{2} + b^{2} - 2ab}{ab (1 - a) (1 - b)} \\ &= \dfrac{(a - b)^{2}}{ab (1 - a) (1 - b)} \ge 0 \quad \Box \end{align} \]