简介
最近公共祖先(lowest common ancestor),简称LCA。定义一个节点同时也是它自己的祖先,那么对于有根树来说,两个节点的公共祖先中离根最远的就是最近公共祖先。
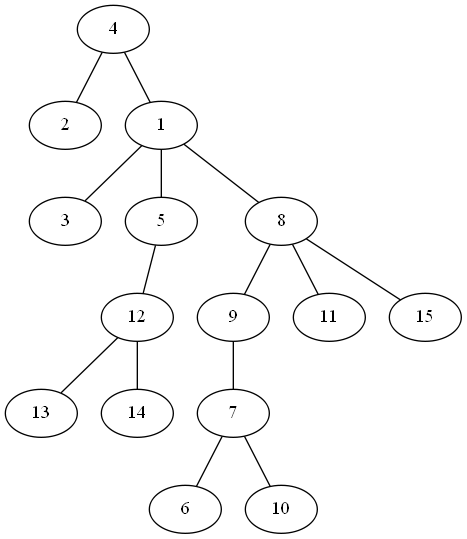
例如,在上面这棵树里,$2, 3$的LCA是$4$,$3, 5$的LCA是$1$,$1, 4$的LCA是$4$。
代码
最朴素的方法当然是让两个节点一步一步往上爬,第一次相遇就得到它们的LCA。比如,求上图中$14, 6$的LCA,那么路径为:
这种暴力解法需要预处理整棵树,时间复杂度$O(n)$,单次查询时间复杂度也是$O(n)$,肯定是不行的。
倍增算法
倍增算法是朴素算法的优化。同样是往上跳,倍增算法从大到小一次跳$2^{n}$个,例如按$8, 4, 2, 1$来跳。
还是求上图中$14, 6$的LCA,路径就简化成了:
前者跳$2$个再跳$1$个,后者直接跳$4$个,得到LCA为$1$。
首先,DFS记录各点的深度及其$2^{n}$的祖先。数组depth表示每个节点的深度,fa[i][j]表示节点$i$的$2^{j}$祖先。1
2
3
4
5
6
7
8
9
10
11
12
13// 树
std::vector<int> g[MAX_SIZE];
// 初始化
int depth[MAXN], fa[MAXN][LOGN];
void dfs(int now, int dad) {
fa[now][0] = dad, depth[now] = depth[dad] + 1;
for (int i = 1; i <= lg[depth[now]]; ++i)
// now的2^i祖先等于2^(n - 1)祖先的2^(n - 1)祖先
fa[now][i] = fa[fa[now][i - 1]][i - 1];
for (int i = 0; i < int(g[now].size()); ++i)
if (g[now][i] != dad)
dfs(g[now][i], now);
}
为了优化,可以对$\log i$做一个预处理:1
2
3
4int lg[MAXN];
lg[1] = 0;
for (int i = 2; i <= n; ++i)
lg[i] = lg[i / 2] + 1;
接下来就是倍增LCA了:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17int lca(int a, int b) {
if (depth[a] < depth[b])
std::swap(a, b);
// 先让a和b跳到同一深度
while (depth[a] > depth[b])
a = fa[a][lg[depth[a] - depth[b]]];
// 如果a等于b,那么它们的LCA必然是a
if (a == b)
return a;
// 向上跳
for (int i = lg[depth[a]]; i >= 0; --i)
// 因为要跳到LCA的下面一层,所以不相等
if (fa[a][i] != fa[b][i])
a = fa[a][i], b = fa[b][i];
// 返回父节点
return fa[a][0];
}
这样,倍增算法的预处理时间复杂度为$O(n \log n)$,单次查询时间复杂度为$O(\log n)$。
RMQ
在树的DFS序中,两个节点的LCA必然不会出现在这两个节点之间,然而LCA的子节点会被包含在内。因此,只需要求DFS序中两个节点之间深度最小的节点,其父节点即为LCA。这样,就把LCA转换成了RMQ问题。
例如,上面的树的DFS序为$4, 2, 1, 3, 5, 12, 13, 14, 8, 9, 7, 6, 10, 11, 15$,求$14, 6$的LCA。介于$14, 6$之间的$8, 9, 7$中,$8$毫无疑问是深度最小的。那么,$8$的父节点$1$就是$14, 6$的LCA。
RMQ问题就可以用ST表解决。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34std::vector<int> g[MAXN];
int f[MAXN][LOGN], lg[MAXN], dfn[MAXN], depth[MAXN], tot;
void dfs(int now, int dad) {
dfn[now] = ++tot, f[tot][0] = dad, depth[now] = depth[dad] + 1;
for (int i = 0; i < int(g[now].size()); ++i)
if (g[now][i] != dad)
dfs(g[now][i], now);
}
void st() {
lg[1] = 0;
for (int i = 2; i <= n; ++i)
lg[i] = lg[i / 2] + 1;
dfs(root, 0);
for (int j = 1; j <= lg[n]; ++j) {
for (int i = 1; i + (1 << j) - 1 <= n; ++i) {
if (depth[f[i][j - 1]] < depth[f[i + (1 << (j - 1))][j - 1]])
f[i][j] = f[i][j - 1];
else
f[i][j] = f[i + (1 << (j - 1))][j - 1];
}
}
}
int lca(int a, int b) {
if (a == b)
return a;
a = dfn[a], b = dfn[b];
if (a > b)
std::swap(a, b);
int len = lg[b - a++];
if (depth[f[a][len]] < depth[f[b - (1 << len) + 1][len]])
return f[a][len];
else
return f[b - (1 << len) + 1][len];
}
RMQ方法求LCA就可以做到预处理$O(n \log n)$,查询$O(1)$。

