学习笔记·函数

映射

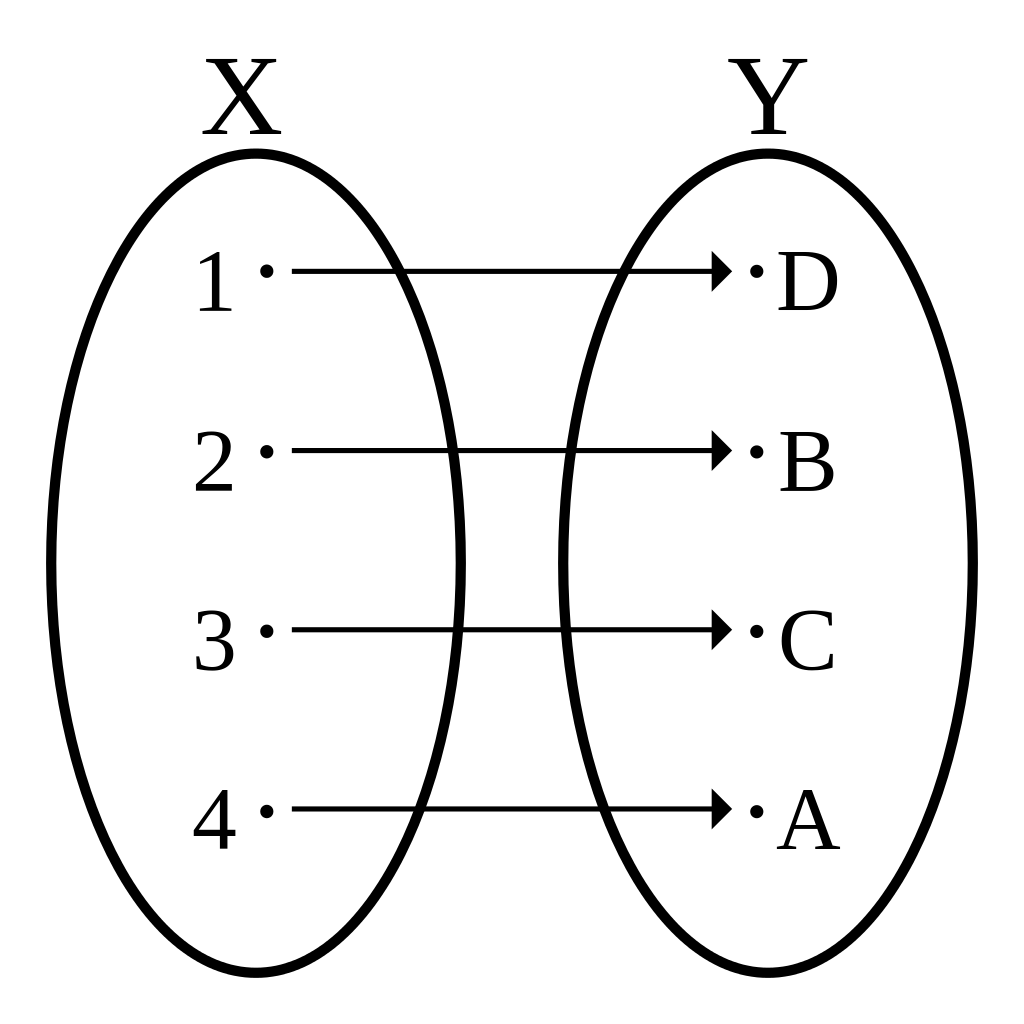
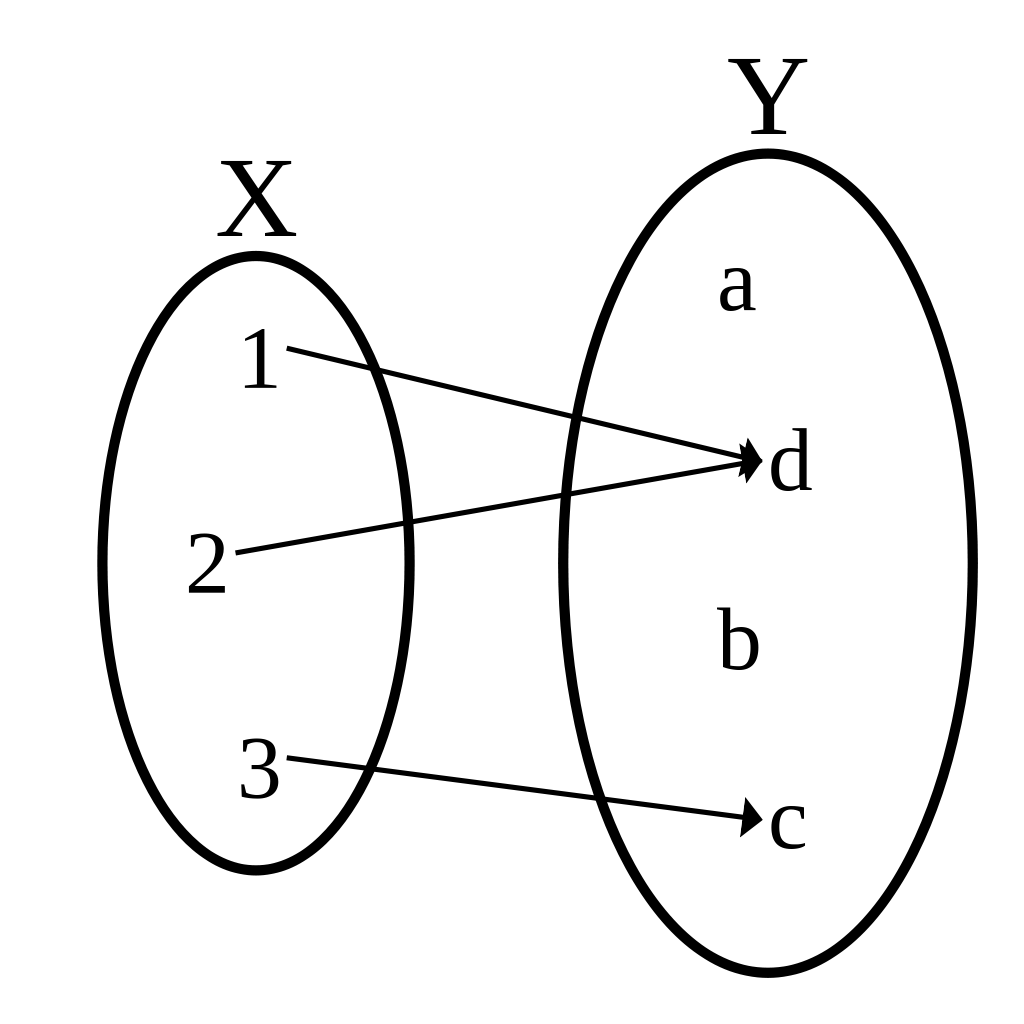
设$A, B$为非空集合，对于任意$x \in A$，通过某种法则$f$，都有$B$中唯一确定的$y$与之对应，则称$f$是一个从$A$到$B$的映射（map），记作$f: A \to B$。
映射$f: A \to B$严格定义为集合$A, B$的笛卡尔积$A \times B = \{(x, y) | x \in A \land y \in B\}$的一个子集，满足对于任意$x \in A$，存在唯一的$y \in B$使得$(x, y) \in f$。

对于一个映射$f: A \to B$，
如果$\forall x, y \in A, f(x) = f(y) \Rightarrow x = y$，那么称$f$为单射（injection）；
如果$\forall y \in B, \exists x \in A, y = f(x)$，那么称$f$为满射（surjection）；
如果映射$f$既是单射又是满射，那么称$f$为双射（bijection）。

如图：

事实上，谓词就是一个把主词映射到$\{T, F\}$的映射。

函数

一般来说，对于映射$f: A \to B$，如果$A, B$是非空的实数集合，那么称$f$是一个从$A$到$B$的函数（function）。
在函数$f$中，$x \in A, y \in B$，$x$与$y$相对应，则称$y$为$x$的像（image），记作$y = f(x)$；$x$为$y$的原像（inverse image），记作$x = f^{-1}(y)$。
集合$A$称为$f$的定义域（domain），$B$称为陪域（codomain），而$A$映射到$B$上的像$f(A)$称为值域（range）。值域是陪域的子集，即$f(A) \subseteq B$。如果函数表达式已知，那么使得函数$f(x)$有意义的$x$的集合称为自然定义域（natural domain）。
平面内的点集$\{(x, f(x)) | x \in A\}$是函数$f$的图像（graph）。

如果两个函数$f, g$的定义域相等，都是$A$，且有$\forall x \in A, f(x) = g(x)$，那么称函数$f, g$相等。例如$f(x) = x$与$g(x) = \sqrt[3]{x^{3}}$就是相等函数。
设函数$f: A \to B, g: B \to C$，$f$与$g$的复合（composition）为$f \circ g: A \to C$，$(f \circ g)(x) = f(g(x))$。

由多个子函数分段定义的函数称为分段函数（piecewise function），如绝对值函数

$$|x| = \begin{cases} x, & x \ge 0 \\ -x, & x < 0 \end{cases}$$

分段函数的定义域是各段函数定义域的并集，值域是各段函数值域的并集。

符号函数（sign function）是一种常用的分段函数：

$$\operatorname{sgn} x = \begin{cases} 1, & x > 0 \\ 0, & x = 0 \\ -1, & x < 0 \end{cases}$$

这样就有$x = (\operatorname{sgn} x) |x|$。

函数的性质

单调性

设函数$f: A \to B, C \subseteq A$，
如果$\forall x, y \in C, x > y \Rightarrow f(x) > f(y)$，那么称$f$在区间$C$上单调递增（monotonically increasing）；
如果$\forall x, y \in C, x < y \Rightarrow f(x) > f(y)$，那么称$f$在区间$C$上单调递减（monotonically decreasing）。
如果函数$f$在定义域$A$上单调递增或单调递减，我们称$f$为增函数（increasing function）或减函数（decreasing function）。增函数与减函数统称单调函数（monotonic function）。

上面的定义都是严格单调（strictly monotone），我们说的单调一般都是指严格单调。
如果把定义中的$>$或$<$换成$\ge$或$\le$，那么称之为不严格单调。

由定义反过来，对于增函数$f$、减函数$g$，$f(x) > f(y) \Rightarrow x > y, g(x) > g(y) \Rightarrow x < y$同样成立。换言之，两者互为充要条件。

（严格）单调函数都是单射。
这个定理可以通过反证法证明：
不妨设$f: A \to B$为增函数，任取$x, y \in A, x \ne y, f(x) = f(y)$。由于$x \ne y$，那么$x > y$或$x < y$。由增函数的定义可知，此时$f(x) > f(y)$或$f(x) < f(y)$，矛盾。因此$f$为单射。
对于减函数的情况，只要考虑函数$g(x) = -f(x)$就好了。$\Box$

设函数$f: A \to B, C \subseteq A$，如果实数$M$满足$\exists x_{0} \in C, f(x_{0}) = M$且$\forall x \in C, f(x) \le M$，那么$M$是区间$C$上的最大值（maximum），$x_{0}$是最大值点（maximum point）；如果是$f(x) \ge M$，那么$M$是区间$C$上的最小值（minimum），$x_{0}$是最小值点（minimum point）。最大值和最小值统称最值（extremum），最大值点和最小值点统称最值点（extremum point）。

显然，对于单调函数$f: [a, b] \to B$，
若$f$为增函数，则最大值为$f(b)$，最小值为$f(a)$；
若$f$为减函数，则最大值为$f(a)$，最小值为$f(b)$。

对称性与奇偶性

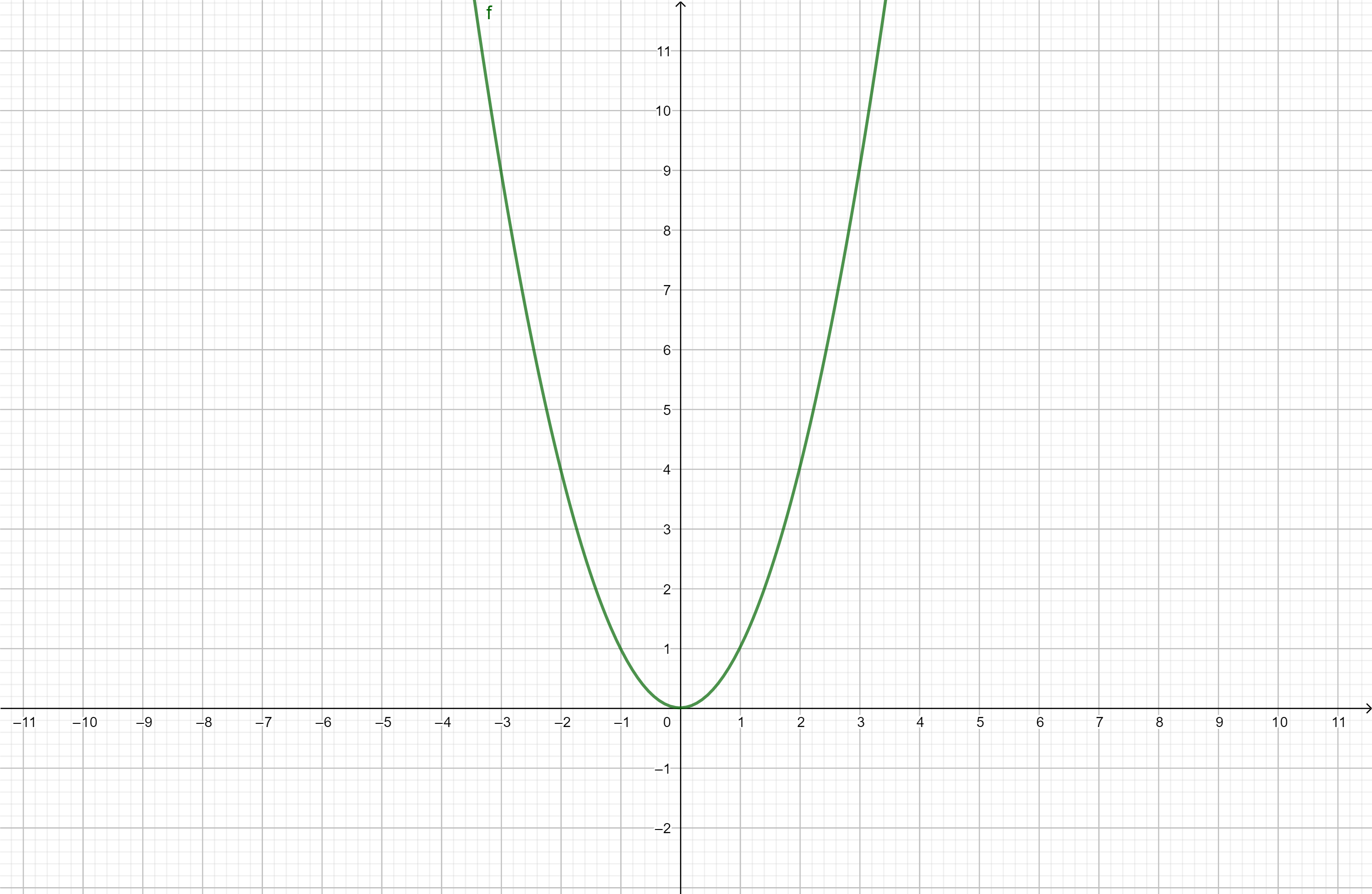
如果一个函数$f: A \to B$的定义域满足$x \in A \Leftrightarrow -x \in A$，且$\forall x \in A, f(x) = f(-x)$，那么称$f$为偶函数（even function）。偶函数的图像关于$y$轴对称。
例如函数$f(x) = x^{2}$，$\forall x \in \mathbb{R}$，都有$f(-x) = (-x)^{2} = x^{2} = f(x)$，因此$f$为偶函数。

不难得到，函数$f(x)$关于直线$x = a$对称的充要条件是$f(a + x) = f(a - x)$。
因此，函数$f(x + a)$为偶函数。

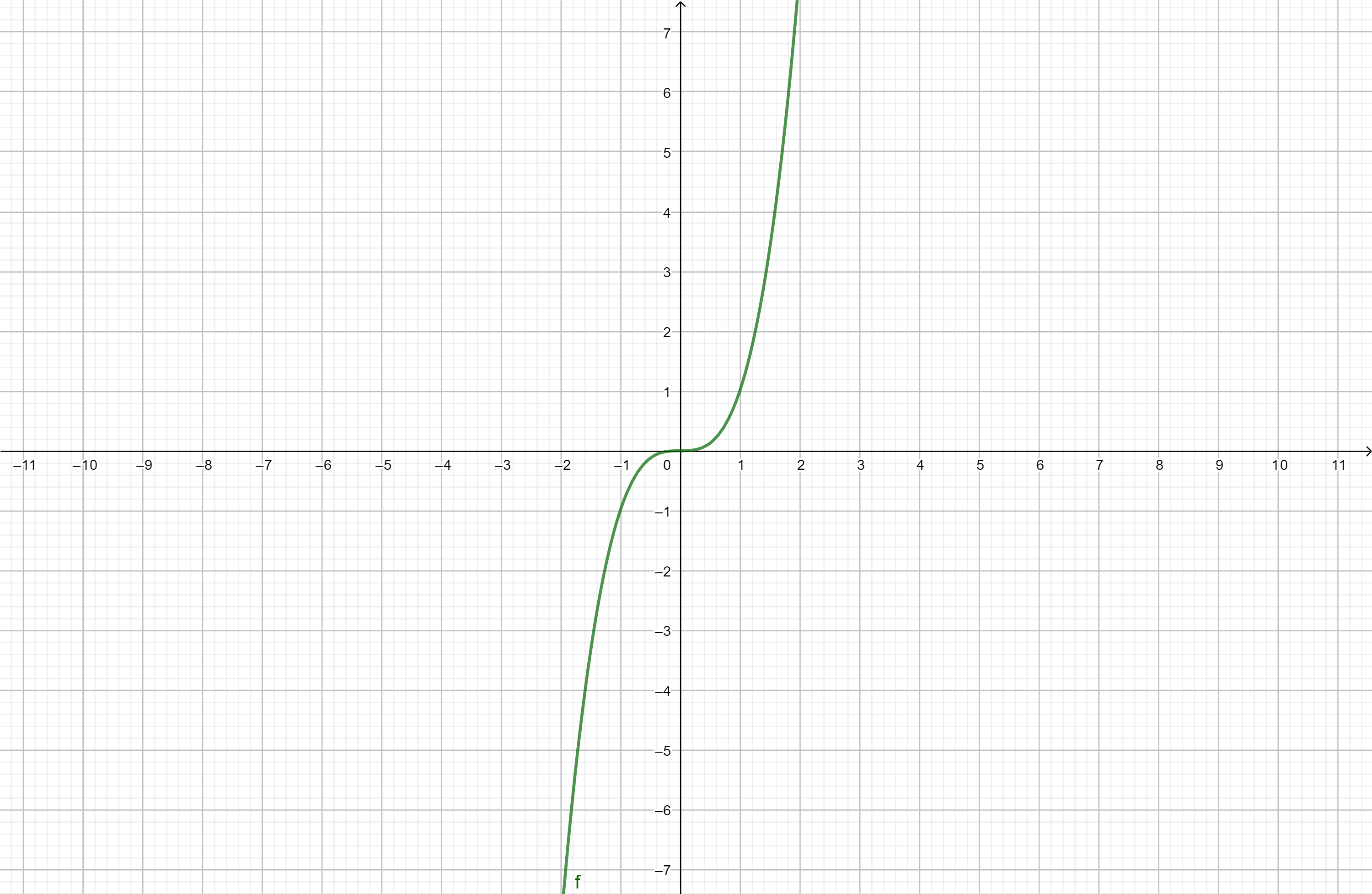
如果一个函数$f: A \to B$的定义域满足$x \in A \Leftrightarrow -x \in A$，且$\forall x \in A, f(-x) = -f(x)$，那么称$f$为奇函数（odd function）。奇函数的图像关于原点中心对称。
例如函数$f(x) = x^{3}$，$\forall x \in \mathbb{R}$，都有$f(-x) = (-x)^{3} = -x^{3} = -f(x)$，因此$f$为奇函数。

不难得到，函数$f(x)$关于点$(a, b)$对称的充要条件是$f(a + x) + f(a - x) = 2b$。
因此，函数$f(x + a) - b$为奇函数。

只有函数$f(x) = 0$同时是奇函数和偶函数。

一般来说，奇函数与偶函数之和为非奇非偶函数；
两个奇函数之和为奇函数，两个偶函数之和为偶函数；
两个奇函数之积为奇函数，两个偶函数之积为偶函数；
两个奇函数之商为奇函数，两个偶函数之商为偶函数；
两个奇函数的复合为奇函数，两个偶函数的复合为偶函数；
奇函数与偶函数之积为奇函数，奇函数与偶函数之商为奇函数，奇函数与偶函数的复合为偶函数。

任意一个定义在关于原点对称的集合上的函数可以唯一地表示为一个奇函数与一个偶函数之和。
证明：
存在性：设任意函数$f(x)$，$f(x) = f_{1}(x) + f_{2}(x)$，其中$f_{1}(x)$为奇函数，$f_{2}(x)$为偶函数，因此

$$f(-x) = f_{1}(-x) + f_{2}(-x) = -f_{1}(x) + f_{2}(x)$$

解关于$f_{1}(x), f_{2}(x)$的方程组

$$\begin{cases} f(x) = f_{1}(x) + f_{2}(x) \\ f(-x) = -f_{1}(x) + f_{2}(x) \end{cases} \Rightarrow \begin{cases} f_{1}(x) = \dfrac{f(x) - f(-x)}{2} \\ f_{2}(x) = \dfrac{f(x) + f(-x)}{2} \end{cases}$$

唯一性：再设$f(x) = g_{1}(x) + g_{2}(x)$，且$g_{1}(x)$为奇函数，$g_{2}(x)$为偶函数，仿照前面推理可得$g_{1}(x) = f_{1}(x), g_{2}(x) = f_{2}(x)$。$\Box$

周期性

对于函数$f$，如果存在一个非零常数$T$，使得定义域内的每一个$x$都有$f(x + T) = f(x)$，那么称$f$为周期函数（periodic function），$T$为函数$f$的周期（period）。
显然，周期不是唯一的。如果所有可能的周期$T$中存在一个最小正数$T_{0}$，那么称$T_{0}$为最小正周期（minimal positive period）。

例如，方波就是一种周期函数：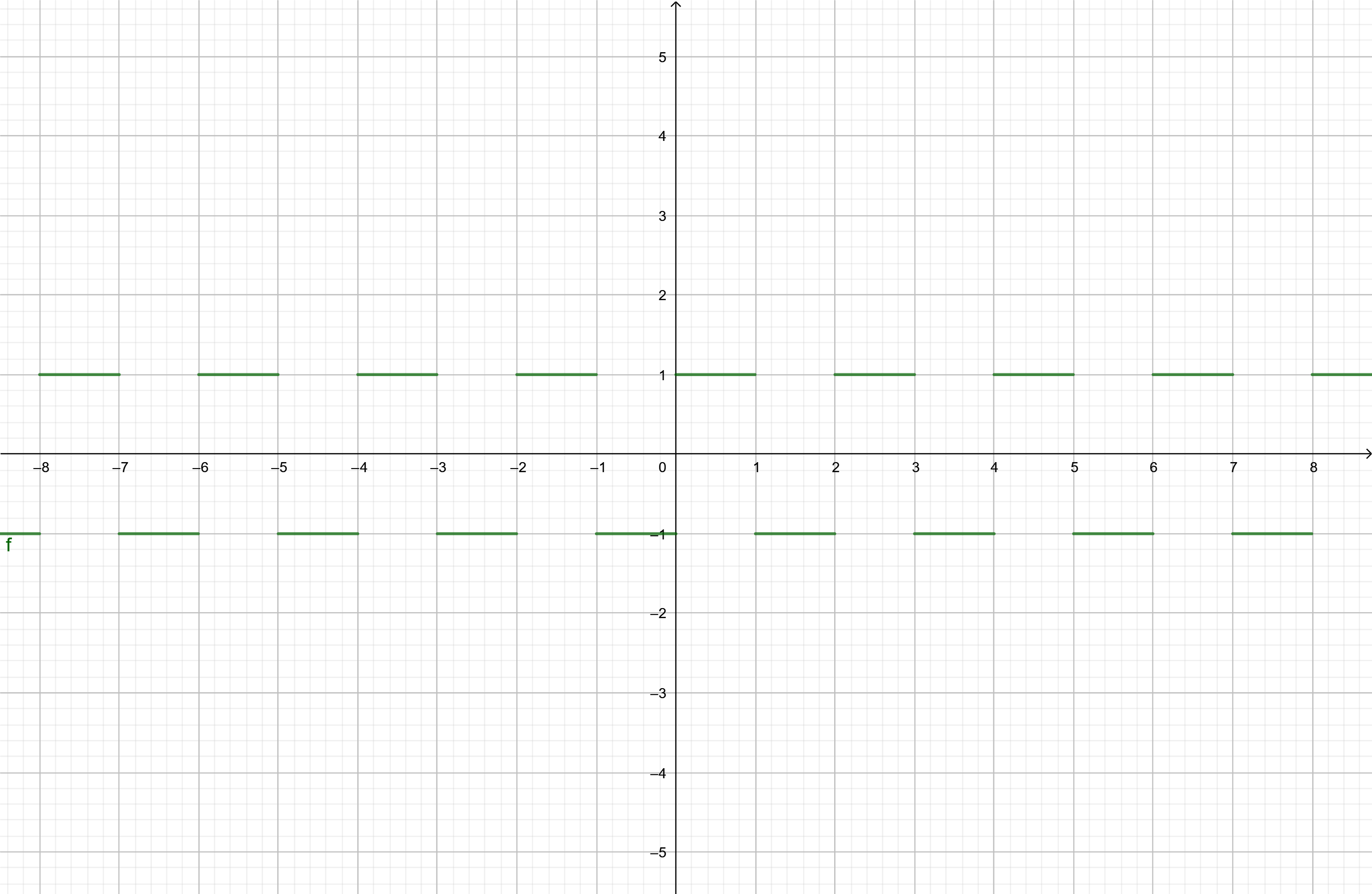

如果周期函数$f$存在最小正周期$T_{0}$，那么对于任何$f$的周期$T$，都存在整数$n$使得$T = n T_{0}$。

连续性

设函数$f: A \to \mathbb{R}, x_{0} \in A$，如果对于任意的$\varepsilon > 0$，都存在$\delta > 0$，使得只要$x \in A, |x - x_{0}| < \delta$，就有$|f(x) - f(x_{0})| < \varepsilon$，那么称$f$在点$x_{0}$连续。
如果函数$f$在定义域$A$的每一点$x_{0}$处都连续，那么称$f$为连续函数（continuous function）。

以上是用$\varepsilon - \delta$语言对函数连续性的定义。
$\varepsilon - \delta$语言最初由法国数学家柯西（Augustin-Louis Cauchy，1789－1857）提出。$\varepsilon$和$\delta$可以看作是两个无穷小量，无论函数值的距离$\varepsilon$多小，都能找到一段长为$\delta$的区间与之对应。

连续函数有一重要性质，即介值定理（intermediate value theorem）：
设连续函数$f: [a, b] \to \mathbb{R}$，$u$为$f(a), f(b)$之间的任意实数，则存在$c \in [a, b]$，使得$f(c) = u$。

如果$f(x) = 0$，$x$称为函数$f$的一个零点（zero point）。
特殊地，$c = 0$时的介值定理称为零点定理：
若$f(a) f(b) < 0$，则存在$c \in (a, b)$使得$f(c) = 0$。

凹凸性

从函数图像上来看，曲线的凹凸决定了函数的凹凸性，所以，我们可以通过几何直观来得到凹凸性的定义：
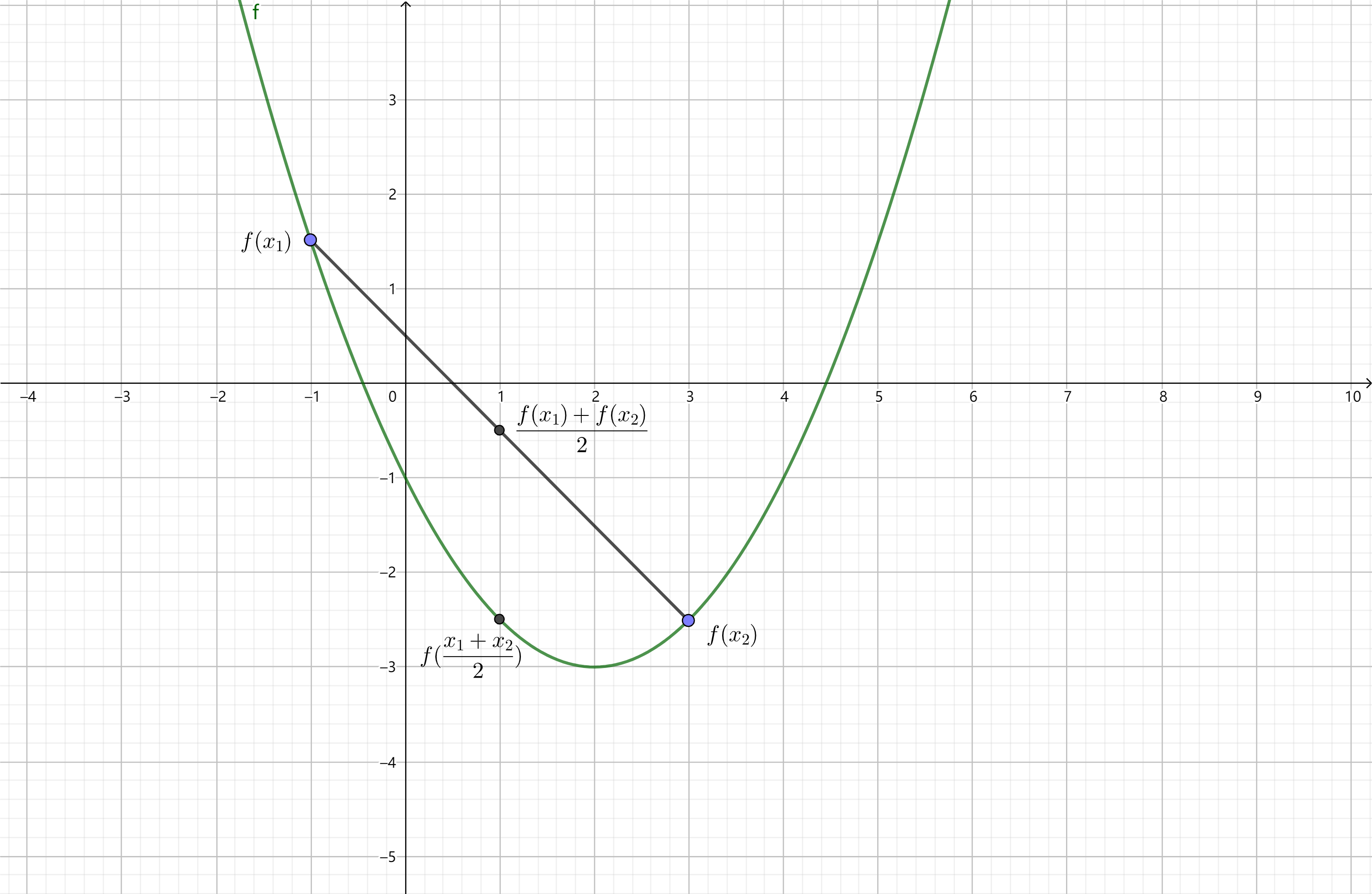
如果在曲线弧上面任意取两点，连接这两点的弦总是在弧段的上方，那么曲线就是凹的，反之类似。取一个特殊的点，即弦的中点，凹凸性可以用弦的中点与曲线弧上具有相同坐标的点的位置关系来描述。

设函数$f$在区间$I$上连续，$\forall x_{1}, x_{2} \in I$，恒有$f(\dfrac{x_{1} + x_{2}}{2}) \le \dfrac{f(x_{1}) + f(x_{2})}{2}$，则称函数在$I$上为凹函数（convex function）或下凸函数；
若恒有$f(\dfrac{x_{1} + x_{2}}{2}) \ge \dfrac{f(x_{1}) + f(x_{2})}{2}$，则称函数在$I$上为凸函数（concave function）或上凸函数。

如果把定义中的$\le$或$\ge$换为$<$或$>$，那么称之为严格凹函数或严格凸函数。

此外，从几何的另一个角度来看，凹凸性的定义也可以表述成这样：
设函数$f$在区间$I$上连续，$\forall x_{1}, x_{2} \in I, \forall \lambda \in (0, 1)$，恒有$f(\lambda x_{1} + (1 - \lambda) x_{2}) \le \lambda f(x_{1}) + (1 - \lambda) f(x_{2})$，则称函数在$I$上为凹函数或下凸函数；
若恒有$f(\lambda x_{1} + (1 - \lambda) x_{2}) \ge \lambda f(x_{1}) + (1 - \lambda) f(x_{2})$，则称函数在$I$上为凸函数或上凸函数。

要理解这个定义，可以先分析下凸的情况，上凸的思考过程类似：
对于下凸的曲线来说，曲线上任意两点间的弧段总是位于这两点连线的下方。
设$(x_{1}, f(x_{1})), (x_{2}, f(x_{2}))$为曲线上两点，则两点连线的方程为

$$g(x) = f(x_{1}) + \dfrac{f(x_{2}) - f(x_{1})}{x_{2} - x_{1}}(x - x_{1})$$

而$x_{1}$与$x_{2}$之间的任意一点$x$可以表示为

$$x = \lambda x_{1} + (1 - \lambda) x_{2}, \lambda \in (0, 1)$$

所以曲线上两点间弧段始终位于两点连线下方等价于

$$f(\lambda x_{1} + (1 - \lambda) x_{2}) \le g(\lambda x_{1} + (1 - \lambda) x_{2})$$

也就是

$$f(\lambda x_{1} + (1 - \lambda) x_{2}) \le \lambda f(x_{1}) + (1 - \lambda) f(x_{2})$$

反函数

如果函数$f: A \to B$是双射的，即值域$B$中每一个元素的原像都是唯一的，那么这个函数就有反函数（inverse function）$f^{-1}$，$(f^{-1} \circ f)(x) = x$。例如函数$f(x) = 2x + 1$，它的反函数为$f^{-1}(x) = \dfrac{x - 1}{2}$。
如果一个函数有反函数，那么称这个函数是可逆的（invertible）。

一个函数有反函数当且仅当是双射函数。
因此，单调函数总是有反函数，并且反函数的单调性与原函数一致。

从图像可以看出来，原函数与反函数的图像关于函数$y = x$的图像对称：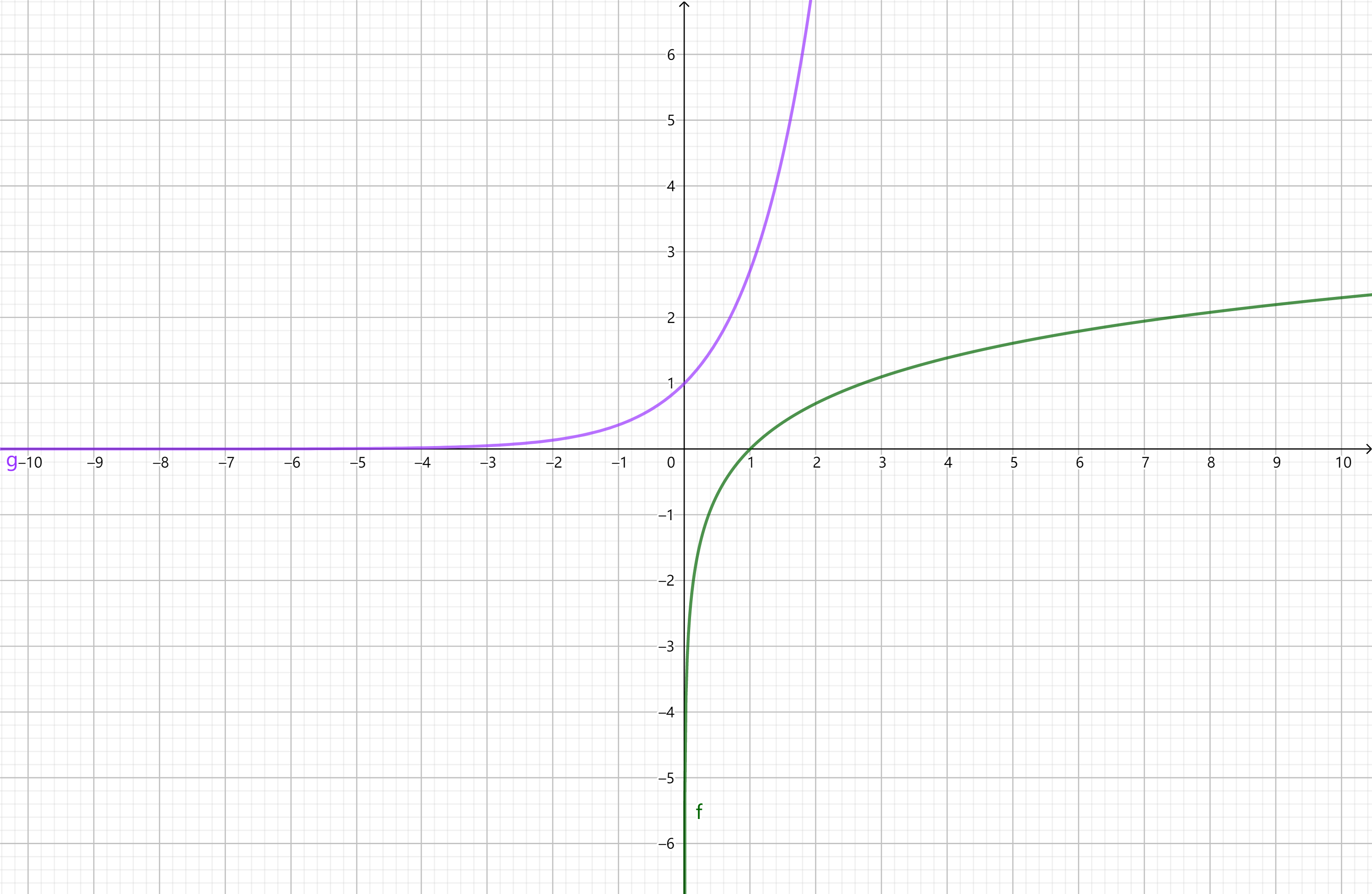

不难发现，原函数的定义域与值域正好是反函数的值域与定义域。

初等函数

幂函数

指数幂

我们已经知道整数指数幂：（$n \in \mathbb{N}^{\ast}$）

$$\begin{align} & a^{n} = \underbrace{a \times a \times \cdots \times a}_{n} \\ & a^{-n} = \dfrac{1}{a^{n}} \ (a \ne 0) \\ & a^{0} = 1 \ (a \ne 0) \end{align}$$

接下来，我们将会扩展指数幂的定义到实数域。

有理数指数幂

设$a, b \in \mathbb{R}, n \in \mathbb{N}^{\ast}$，若满足$b^{n} = a$，则称$b$为$a$的$n$次方根（$n$-th root），记作$b = \sqrt[n]{a}$，也记作$b = a^{\frac{1}{n}}$。

$n$为奇数时，$b$是唯一的，$a$正则$b$正，$a$负则$b$负，$a = 0$则$b = 0$。
$n$为偶数时，须分三种情况讨论：
$a > 0$时，$b$有两值，互为相反数，分别为$\sqrt[n]{a}$与$-\sqrt[n]{a}$；
$a = 0$时，$b = 0$；
$a < 0$时，$b$不存在。

由定义可得，$(a^{\frac{1}{n}})^{n} = a$。
我们可以接着得到：
若$n$为奇数，则$(a^{n})^{\frac{1}{n}} = a$；
若$n$为偶数，则$(a^{n})^{\frac{1}{n}} = |a|$。

对于$a \in \mathbb{R}, m \in \mathbb{Z}, n \in \mathbb{N}^{\ast}$，如果$a^{\frac{1}{n}}$有定义，那么定义$a$的$\dfrac{m}{n}$次幂为：

$$a^{\frac{m}{n}} = (a^{m})^{\frac{1}{n}} = \sqrt[n]{a^{m}}$$

实数指数幂

无理数指数幂比较难定义，我们以$5^{\sqrt{2}}$为例：

通过计算器可以得知，$\sqrt{2} = 1.414213562\cdots$。
我们取不同的小数点后位数的不足近似值$n$来计算$5^{n}$：

小数点后位数	不足近似值$n$	$5^{n}$
1	1.4	9.518269694
2	1.41	9.672699729
3	1.414	9.735171039
4	1.4142	9.738305174
5	1.41421	9.738461907
6	1.414213	9.738508928
7	1.4142135	9.738516765
8	1.41421356	9.738517705
9	1.414213562	9.738517736

可以发现，随着$n$逐渐增大逼近$\sqrt{2}$，$5^{n}$趋向于一个固定的值，这个值就是$5^{\sqrt{2}}$。

对于实数指数幂，我们有以下运算法则：（$a \in \mathbb{R^{+}}, m, n \in \mathbb{R}$）

$$\begin{align} & a^{m} \cdot a^{n} = a^{m + n} \\ & a^{m} \cdot b^{m} = (ab)^{m} \\ & (a^{m})^{n} = a^{mn} \end{align}$$

幂函数

幂函数（power function）：

$$f(x) = x^{\alpha}, \alpha \in \mathbb{R}$$

先来考察$\alpha \in \mathbb{Q}$时幂函数的定义域。
将$\alpha$表示为分数形式，设$\alpha = \dfrac{p}{q}$，由有理数指数幂的定义可以得到：
若$p > 0$且$q$为奇数，则定义域为$\mathbb{R}$；
若$p > 0$且$q$为偶数，则定义域为$[0, +\infty)$；
若$p < 0$且$q$为奇数，则定义域为$\{x | x \ne 0\}$；
若$p < 0$且$q$为偶数，则定义域为$(0, +\infty)$。

$\alpha$为无理数时比较复杂。因为$x < 0$时截取的近似值$\alpha_{n}$用分数形式表示分母可能为偶数，一般认为$\alpha$为正无理数时定义域为$[0, +\infty)$，而负无理数为$(0, +\infty)$。

分别取$\alpha = 1, 2, 3, -1, \dfrac{1}{2}$时画出图像：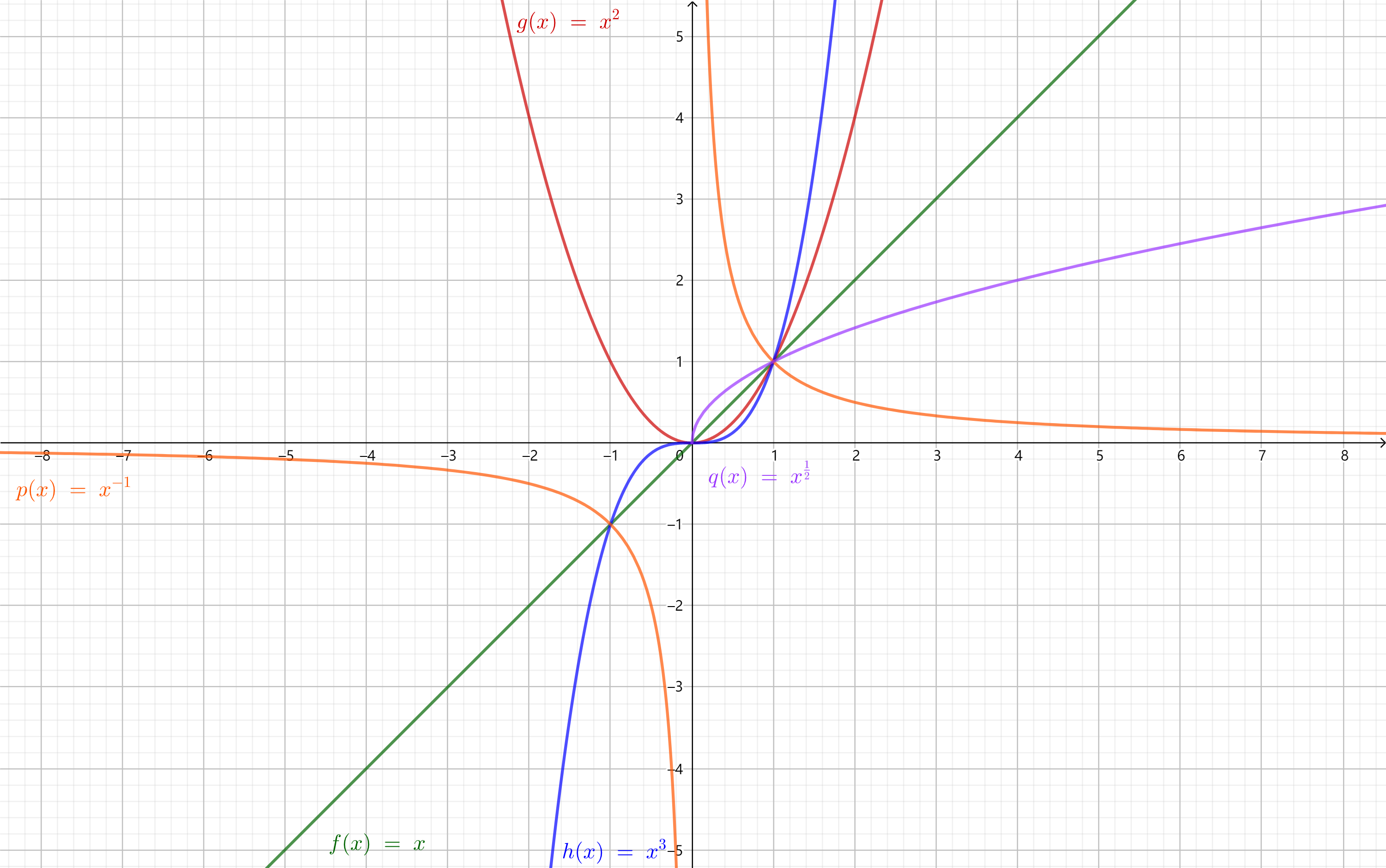

从图中可以发现，幂函数在第一象限总是有定义，并且恒过定点$(1, 1)$。

考察幂函数的单调性：
可以证明，
$\alpha > 0$时，幂函数在$(0, +\infty)$上为增函数；
$\alpha < 0$时，幂函数在$(0, +\infty)$上为减函数。

奇偶性：
设$\alpha = \dfrac{p}{q}$，如果$q$为奇数，$p$为奇数则为奇函数，$p$为偶数则为偶函数。
（$q = \pm1$时实际上就是$\alpha$为奇数时则为奇函数，$\alpha$为偶数时则为偶函数）

看这张动图会更容易理解一些：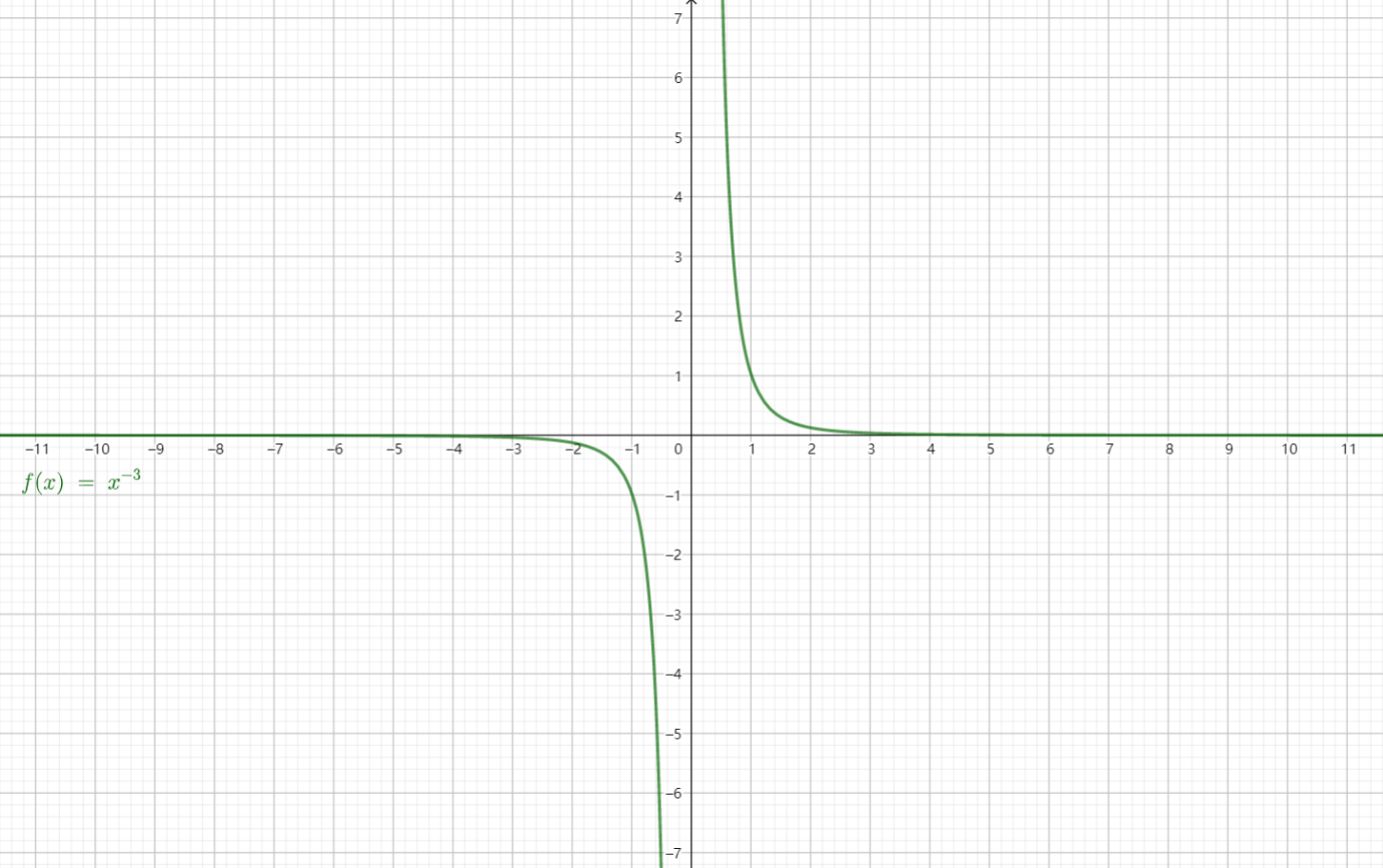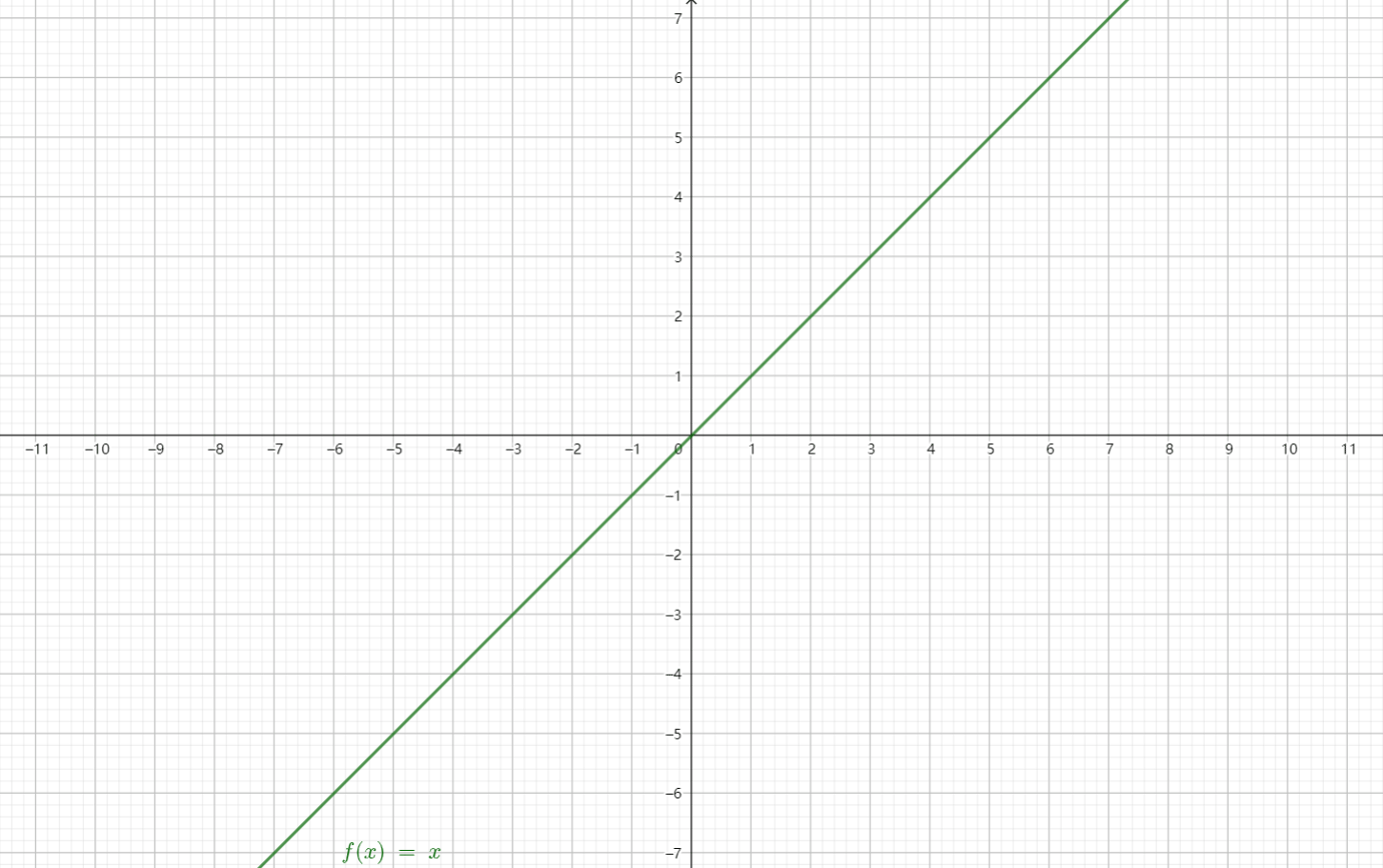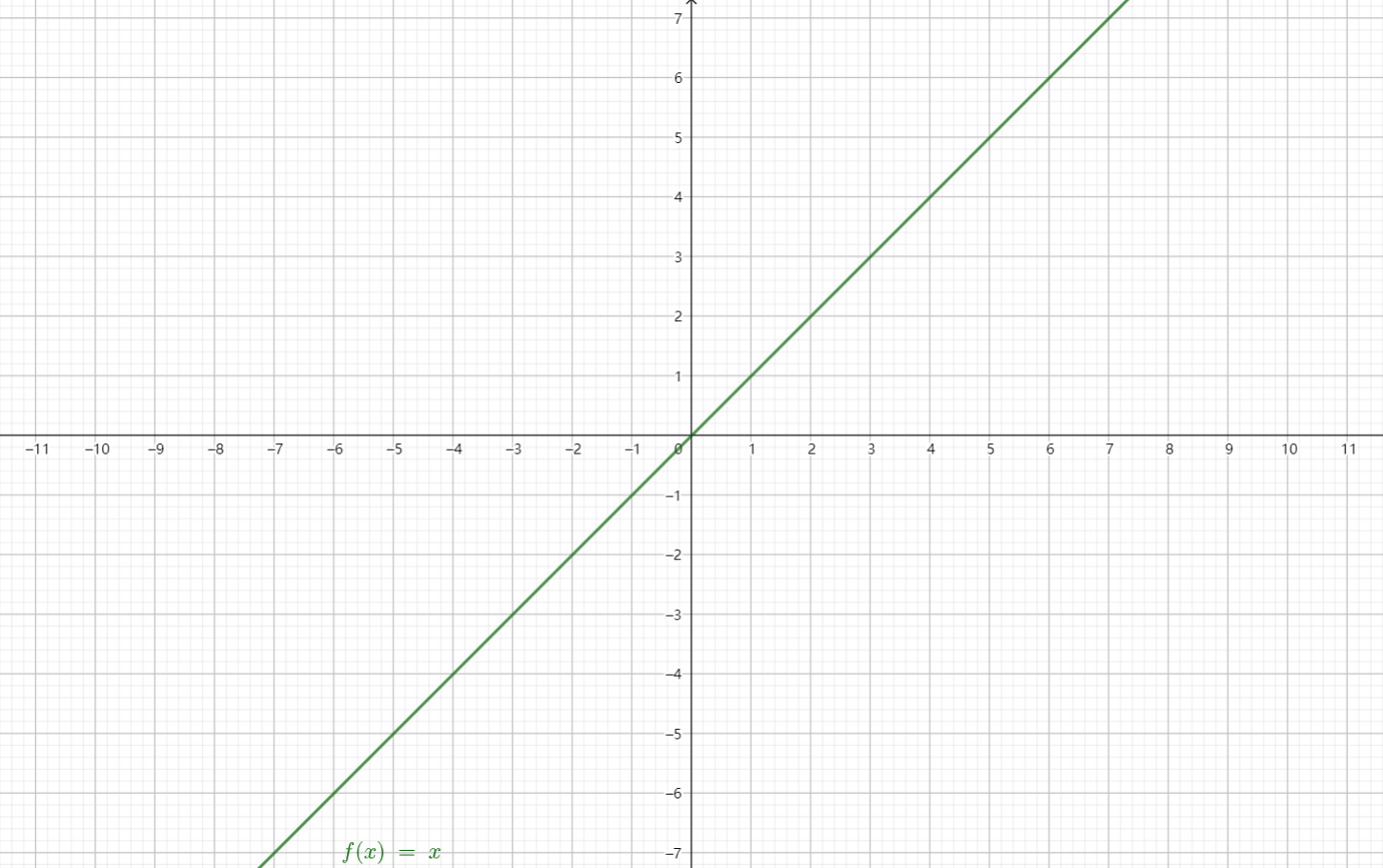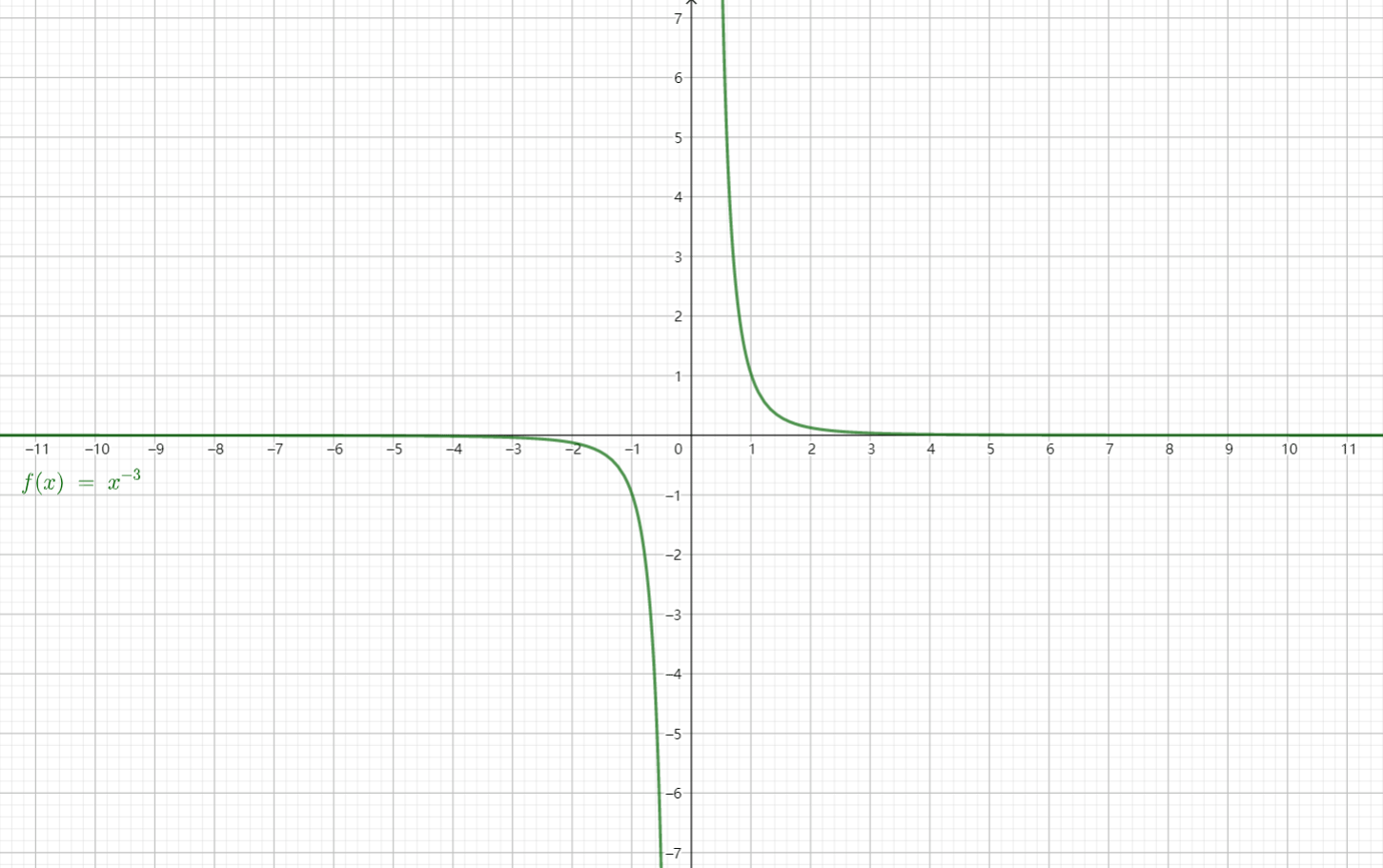

指数函数

指数函数（exponential function）：

$$f(x) = a^{x}, a > 0, a \ne 1$$

因为$a > 0$，指数函数的定义域为$\mathbb{R}$，值域为$(0, +\infty)$。

根据图像，
若$a > 1$，则指数函数为增函数；
若$0 < a < 1$，则指数函数为减函数。

证明如下：
设$f(x) = a^{x}, a > 1, x_{1} < x_{2}$，有

$$\dfrac{f(x_{1})}{f(x_{2})} = a^{x_{1} - x_{2}}$$

设$g(x) = x^{x_{1} - x_{2}}$，
我们知道$g(x)$是幂函数，由于$x_{1} - x_{2} < 0$，$g(x)$在$(0, +\infty)$上单调递减，因此

$$a^{x_{1} - x_{2}} = g(a) < g(1) = 1$$

故$f(x_{1}) < f(x_{2})$，$f(x)$为增函数。
$0 < a < 1$时考虑$f(x) = (\dfrac{1}{a})^{x}$即可。$\Box$

由于$(\dfrac{1}{a})^{x} = a^{-x}$，底数互为倒数的两个指数函数的图像关于$y$轴对称。
指数函数的图像总是通过点$(0, 1)$。

指数函数中，有一种函数特别重要：

$$f(x) = \mathrm{e}^{x}$$

$\mathrm{e}$是一个无理数，近似值为

$$\mathrm{e} = 2.71828\cdots$$

对数函数

对数

设$a^{b} = c$，那么$b$称为以$a$为底$c$的对数（logarithm），记作

$$b = \log_{a} c$$

其中$a$称为对数的底数（base），$c$称为真数（antilogarithm）。

设指数函数$f(x) = a^{x}$，对数函数就是指数函数的反函数$f^{-1}(x) = \log_{a} x$。
同样，$a > 0, a \ne 1$。

以$10$为底的对数称作常用对数（common logarithm），记作$\lg$；
以$\mathrm{e}$为底的对数称作自然对数（natural logarithm），记作$\ln$。

由对数的定义可得：

$$\begin{align} & a^{\log_{a} x} = x \\ & \log_{a} a^{x} = x \end{align}$$

由对数与指数的关系，可得对数的运算性质：（$a > 0, a \ne 1, m, n > 0, b \in \mathbb{R}$）

$$\begin{align} & \log_{a} (m n) = \log_{a} m + \log_{a} n \\ & \log_{a} \dfrac{m}{n} = \log_{a} m - \log_{a} n \\ & \log_{a} m^{b} = b \log_{a} m \end{align}$$

设$\log_{a} b = x$，则$a^{x} = b$，
可得$\log_{c} a^{x} = \log_{c} b$，
再根据运算性质得$x \log_{c} a = \log_{c} b$，
即得换底公式：

$$\log_{a} b = \dfrac{\log_{c} b}{\log_{c} a}$$

特别地，$\log_{a} b \cdot \log_{b} a = 1$。

对数函数

对数函数（logarithm function）：

$$f(x) = \log_{a} x, a > 0, a \ne 1$$

由于对数函数是指数函数的反函数，很多性质可以由指数函数得出。

对数函数与指数函数的定义域与值域对调，
对数函数的定义域为$(0, +\infty)$，值域为$\mathbb{R}$。

$a > 1$时，对数函数为增函数；
$0 < a < 1$时，对数函数为减函数。

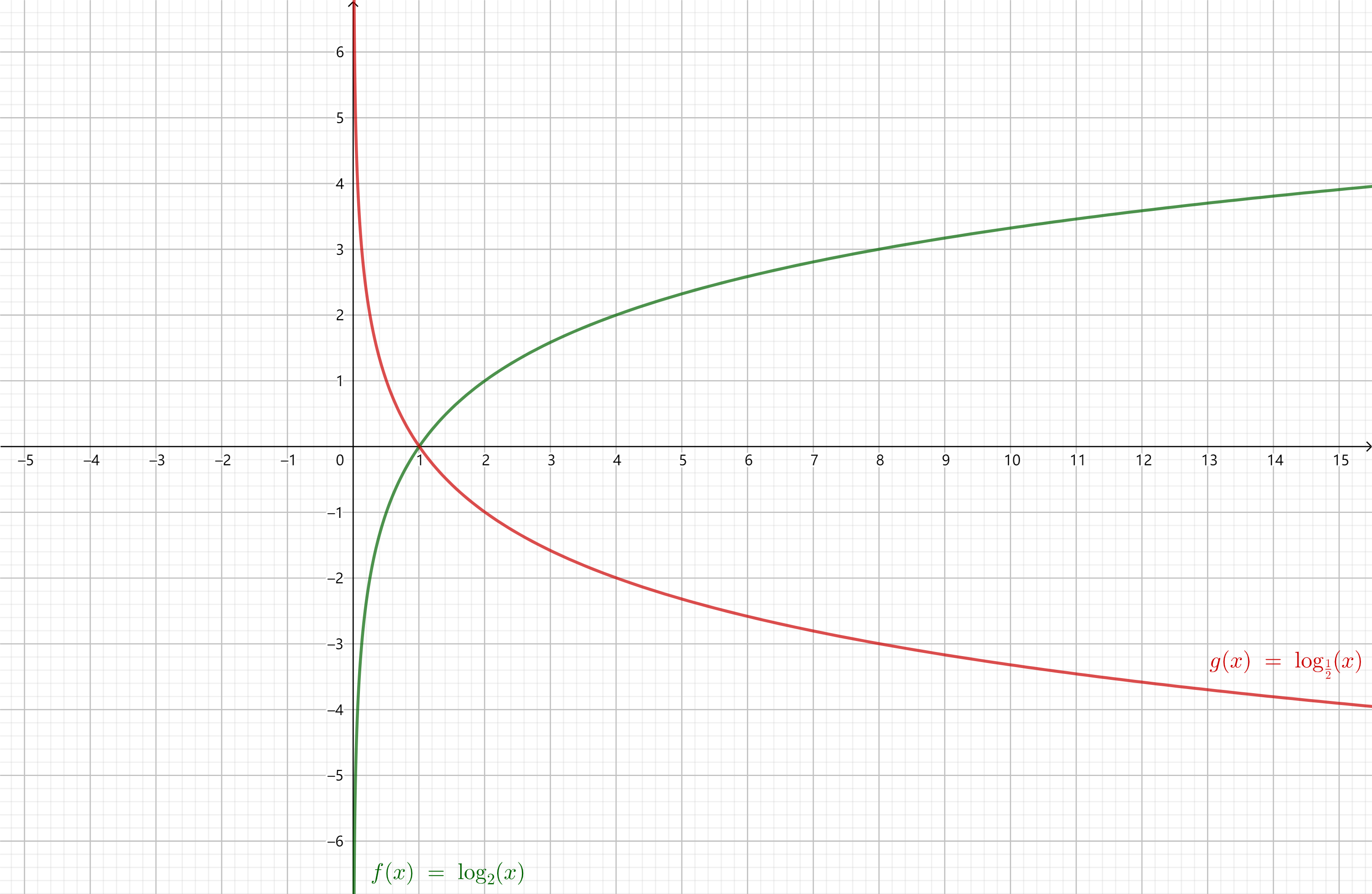
由于$\log_{\frac{1}{a}} x = -\log_{a} x$，底数互为倒数的两个对数函数的图像关于$x$轴对称。
对数函数的图像总是通过点$(1, 0)$。

三角函数

任意角

一条射线绕其端点逆时针旋转形成的角叫做正角，顺时针旋转形成的角叫做负角，不做旋转形成的角叫做零角。
将周角分为$360$份，那么每一份都是$1^{\circ}$。
如果正角$\alpha$含有$x$份，那么$\alpha = x^{\circ}$；
如果负角$\beta$含有$y$份，那么$\beta = -y^{\circ}$；
任意零角$\gamma = 0^{\circ}$。
两个旋转方向和旋转量相同的角$\alpha, \beta$是相等的，记作$\alpha = \beta$。

定义角的加法$\alpha + \beta$为角$\alpha$的终边旋转角$\beta$所得的角，
减法$\alpha - \beta = \alpha + (-\beta)$。

显然，所有与角$\alpha$终边相同的角都可以表示为$\alpha$与整数个周角之和。

在平面直角坐标系内，使角的顶点与原点重合，角的始边与$x$非负半轴重合，那么，根据终边的位置在第一、二、三、四象限，分别称之为第一、二、三、四象限角。
容易求出角$\alpha$是第一、二、三、四象限角的充要条件：

1. $k \in \mathbb{Z}, k \cdot 360^{\circ} < \alpha < k \cdot 360^{\circ} + 90^{\circ}$
2. $k \in \mathbb{Z}, k \cdot 360^{\circ} + 90^{\circ} < \alpha < k \cdot 360^{\circ} + 180^{\circ}$
3. $k \in \mathbb{Z}, k \cdot 360^{\circ} + 180^{\circ} < \alpha < k \cdot 360^{\circ} + 270^{\circ}$
4. $k \in \mathbb{Z}, k \cdot 360^{\circ} + 270^{\circ} < \alpha < (k + 1) \cdot 360^{\circ}$

不是象限角的角，即终边在坐标轴上的角称为轴线角。
一个周角范围内，轴线角有零角、直角、平角、$270^{\circ}$角和周角。

弧度制

以$1^{\circ}$为周角的$\dfrac{1}{360}$来度量角的单位制为角度制，
而在弧度制中，
$1$弧度（radian）定义为长度等于半径的圆弧所对的圆心角，记作$1 \ \mathrm{rad}$，弧度单位$\mathrm{rad}$通常省略不写。
这样，周角就是$2 \pi$，平角就是$\pi$，$1^{\circ}$就是$\dfrac{\pi}{180}$。

在半径为$r$的圆中，弧长为$l$的圆弧所对的圆心角为$\alpha \ \mathrm{rad}$，那么

$$|\alpha| = \dfrac{l}{r}$$

三角函数的概念

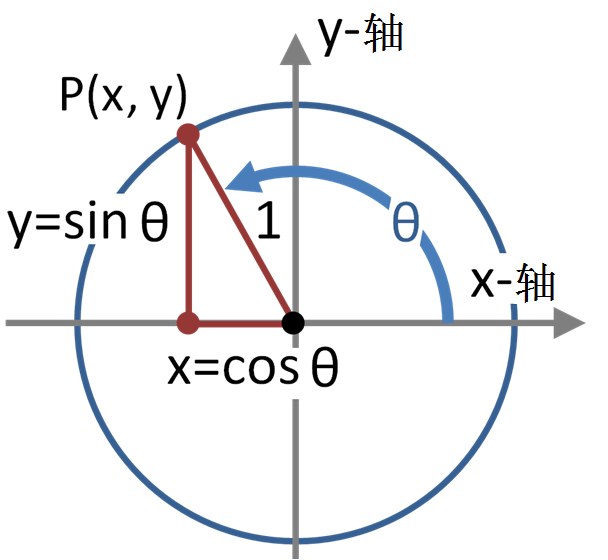
以原点为圆心，作一个半径为$1$的单位圆。设角$\alpha$的始边为$x$非负半轴，终边与单位圆的交点是$P(x, y)$。对于一个确定的$\alpha$，$x$和$y$都是唯一确定的。定义：

• 角$\alpha$的正弦（sine）：$\sin \alpha = y$
• 角$\alpha$的余弦（cosine）：$\cos \alpha = x$
• 角$\alpha$的正切（tangent）：$\tan \alpha = \dfrac{y}{x}$

特别注意，当$\alpha = k \pi + \dfrac{\pi}{2} (k \in \mathbb{Z})$时，角$\alpha$的终边在$y$轴上，此时$x = 0$，$\tan \alpha$没有定义。

正弦、余弦和正切是最重要的三个三角函数（trigonometric function）。

此外，还有三个较少用到的三角函数，分别是正弦、余弦和正切的倒数：

• 角$\alpha$的余割（cosecant）：$\csc \alpha = \dfrac{1}{y}$
• 角$\alpha$的正割（secant）：$\sec \alpha = \dfrac{1}{x}$
• 角$\alpha$的余切（cotangent）：$\cot \alpha = \dfrac{x}{y}$

同样，在$\alpha = k \pi (k \in \mathbb{Z})$时，$\cot \alpha$和$\csc \alpha$没有定义；$\alpha = k \pi + \dfrac{\pi}{2} (k \in \mathbb{Z})$时，$\sec \alpha$没有定义。

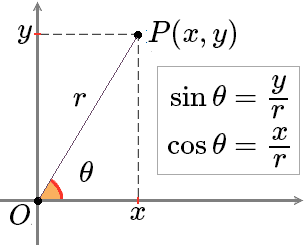
在平面直角坐标系中，设角$\alpha$的始边为$x$非负半轴，终边上一点坐标为$P(x, y)$，$|OP| = r$。
作单位圆，通过相似三角形可以证得

$$\sin \alpha = \dfrac{y}{r}, \cos \alpha = \dfrac{x}{r}, \tan \alpha = \dfrac{y}{x}$$

由勾股定理可知$r = \sqrt{x^{2} + y^{2}}$，因此只要知道角$\alpha$终边上任意一点坐标，就可以求得其所有三角函数值。

由这一点可以推出，
第一、二、三、四象限角，其
正弦函数的符号分别为正、正、负、负，
余弦函数的符号分别为正、负、负、正，
正切函数的符号分别为正、负、正、负。

以上对三角函数的定义都是依赖几何直观的，而数学家用泰勒级数给出了不依赖几何直观的代数定义：

$$\begin{align} & \sin x = x - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + \cdots \\ & \cos x = 1 - \dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + \cdots \end{align}$$

用求和符号表示就是

$$\begin{align} & \sin x = \sum\limits_{n=0}^{\infty} \dfrac{(-1)^{n} x^{2n + 1}}{(2n + 1)!} \\ & \cos x = \sum\limits_{n=0}^{\infty} \dfrac{(-1)^{n} x^{2n}}{(2n)!} \end{align}$$

在精度要求不是很高的情况下，我们可以取这个式子的前几项粗略地计算三角函数值，$x$越小精度越高。

同角三角函数关系式

由三角函数的定义可以得到

$$\tan \alpha = \dfrac{\sin \alpha}{\cos \alpha} (\alpha \ne k \pi + \dfrac{\pi}{2}, k \in \mathbb{Z})$$

设角$\alpha$的始边为$x$非负半轴，终边与单位圆的交点是$P(x, y)$。
过$P$作$x$轴的垂线，垂足为$M$，则勾股定理有

$$|OM|^{2} + |MP|^{2} = |OP|^{2} = 1$$

故

$$x^{2} + y^{2} = 1$$

即毕达哥拉斯三角恒等式（Pythagorean trigonometric identity）

$$\sin^{2} \alpha + \cos^{2} \alpha = 1$$

从这两个公式还能得到很多公式，可以用一个六边形形象地概括：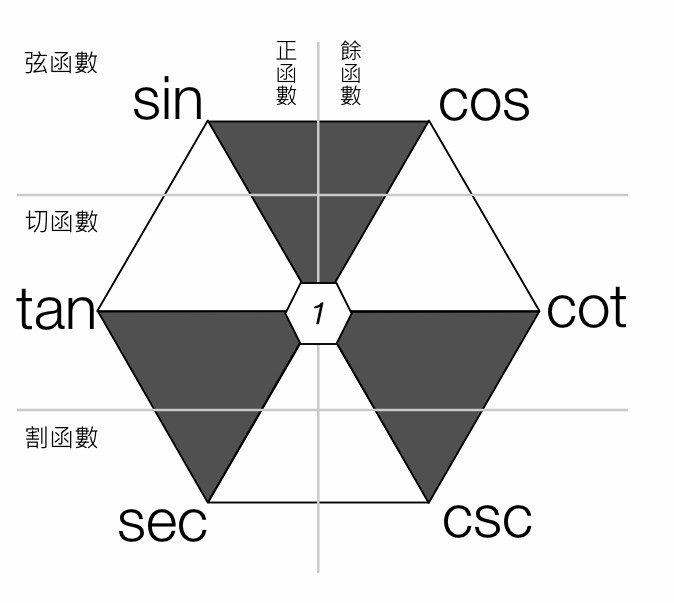

• 六边形每个顶点上的三角函数等于相邻两个顶点上三角函数的乘积
  例如：$\cos \alpha = \sin \alpha \cot \alpha$
• 六边形相对的两个顶点上的三角函数乘积等于$1$
  例如：$\sin \alpha \csc \alpha = 1$
• 三个阴影三角形中，上面两个顶点的平方和等于下面顶点的平方
  例如：$1 + \cot^{2} \alpha = \csc^{2} \alpha$

诱导公式

两个相差$2 k \pi (k \in \mathbb{Z})$的角，终边一定是相等的，因此它们的三角函数值也一定相等，即
诱导公式一：

$$\begin{align} & \sin(2 k \pi + \alpha) = \sin \alpha \\ & \cos(2 k \pi + \alpha) = \cos \alpha \\ & \tan(2 k \pi + \alpha) = \tan \alpha \end{align}$$

如果两个角相差$\pi$，那么其终边与单位圆的交点关于原点对称，此时两点的横坐标和纵坐标互为相反数。由三角函数定义可得
诱导公式二：

$$\begin{align} & \sin(\pi + \alpha) = -\sin \alpha \\ & \cos(\pi + \alpha) = -\cos \alpha \\ & \tan(\pi + \alpha) = \tan \alpha \end{align}$$

同样，结合单位圆，可以得到
诱导公式三：

$$\begin{align} & \sin(-\alpha) = -\sin \alpha \\ & \cos(-\alpha) = \cos \alpha \\ & \tan(-\alpha) = -\tan \alpha \end{align}$$

诱导公式四：

$$\begin{align} & \sin(\pi - \alpha) = \sin \alpha \\ & \cos(\pi - \alpha) = -\cos \alpha \\ & \tan(\pi - \alpha) = -\tan \alpha \end{align}$$

这四条公式足以把所有三角函数都转化为锐角三角函数进行计算：
任取一角$\alpha = 2 k \pi + \beta, k \in \mathbb{Z}, \beta \in [0, 2 \pi)$，使用公式一将其转化为$\beta$的三角函数。如果是负角，也可以先使用公式三。

1. 如果$\beta \in [\pi, 2\pi)$，使用公式二，转化为$[0, \pi)$的三角函数；
2. 如果$\beta \in [\dfrac{\pi}{2}, \pi)$，使用公式四，转化为$[0, \dfrac{\pi}{2})$即锐角三角函数。

已知角$\alpha$，求$k \pi + \alpha (k \in \mathbb{Z})$的三个三角函数值。

• 如果$k$是偶数
  那么$\sin(k \pi + \alpha) = \sin \alpha$
  同理，$\cos(k \pi + \alpha) = \cos \alpha, \tan(k \pi + \alpha) = \tan \alpha$
• 如果$k$是奇数，则$k - 1$是偶数
  那么$\sin(k \pi + \alpha) = \sin(2 \cdot \dfrac{k - 1}{2} + \pi + \alpha) = \sin(\pi + \alpha) = -\sin \alpha$
  同理，$\cos(k \pi + \alpha) = -\cos \alpha, \tan(k \pi + \alpha) = \tan \alpha$

由此可得

$$\begin{align} & \sin(k \pi + \alpha) = (-1)^{k} \sin \alpha \\ & \cos(k \pi + \alpha) = (-1)^{k} \cos \alpha \\ & \tan(k \pi + \alpha) = \tan \alpha \end{align}$$

如果两个角和为$\dfrac{\pi}{2}$，那么其终边与单位圆的交点关于直线$y = x$对称，此时两点的横坐标和纵坐标互换。由三角函数定义可得
诱导公式五：

$$\begin{align} & \sin(\dfrac{\pi}{2} - \alpha) = \cos \alpha \\ & \cos(\dfrac{\pi}{2} - \alpha) = \sin \alpha \\ & \tan(\dfrac{\pi}{2} - \alpha) = \cot \alpha \end{align}$$

类似地，可以得到
诱导公式六：

$$\begin{align} & \sin(\dfrac{\pi}{2} + \alpha) = \cos \alpha \\ & \cos(\dfrac{\pi}{2} + \alpha) = -\sin \alpha \\ & \tan(\dfrac{\pi}{2} + \alpha) = -\cot \alpha \end{align}$$

用这两条公式可以化简更多的三角函数，例如

$$\sin(\dfrac{3\pi}{2} - \alpha) = \sin(\pi + \dfrac{\pi}{2} - \alpha) = -\sin(\dfrac{\pi}{2} - \alpha) = -\cos \alpha$$

这些公式可以总结为$\dfrac{k \pi}{2} \pm \alpha (k \in \mathbb{Z})$的三角函数，用一个口诀概括就是：奇变偶不变，符号看象限。
$k$为奇数时，$\sin$变为$\cos$，$\cos$变为$\sin$，$\tan$变为$\cot$；而$k$为偶数时，三角函数不变。
正负号可以先看角$\dfrac{k \pi}{2} \pm \alpha$的终边在哪一象限，再通过原三角函数在该象限的符号确定。

三角函数的图像与性质

正弦函数与余弦函数

以函数$f(x) = \sin x$为例，要画出它的图像，要从定义出发。
在单位圆上作出弧度为$x_{0}$的角，终边交单位圆于点$B$。根据正弦函数的定义，点$B$的纵坐标$y_{0} = \sin x_{0}$。以$x_{0}$为横坐标，$y_{0}$为纵坐标，即可得到函数图像上的点$T(x_{0}, \sin x_{0})$。
画出足够多的点并用光滑的曲线连接起来，我们就得到了正弦函数的图像，即正弦曲线（sinusoid）。

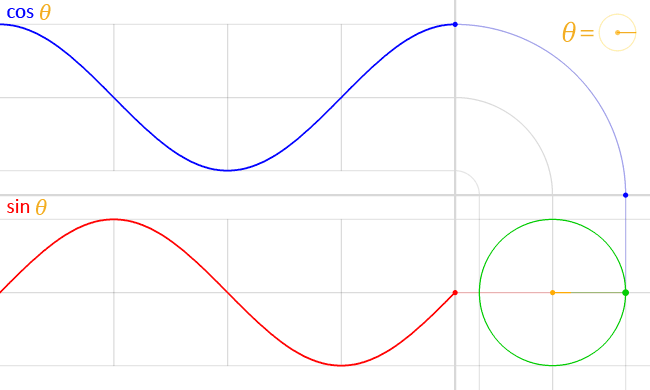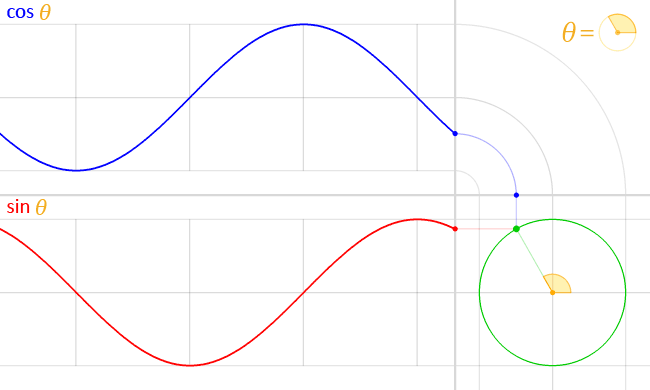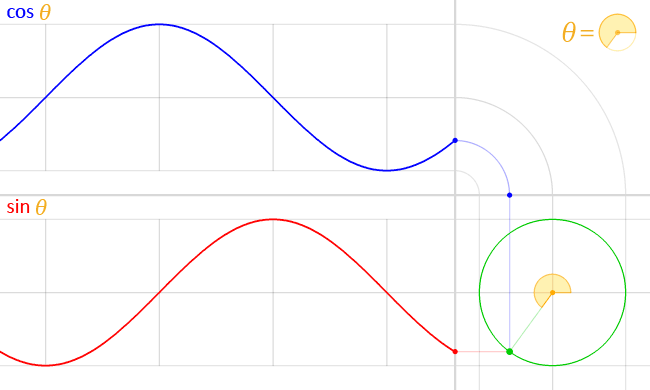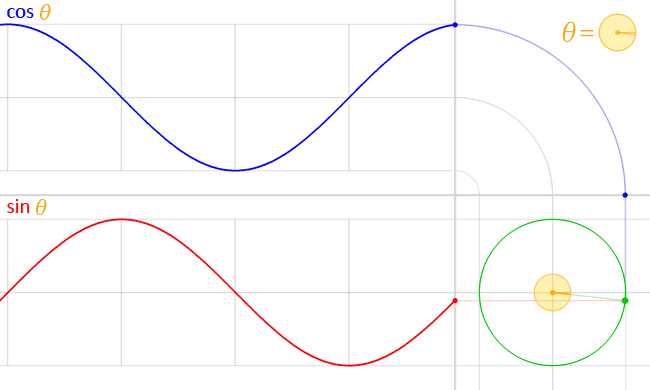
实际上，我们只要画出$[0, 2 \pi]$上的图像，然后根据诱导公式一，将这个图像不断地向左右平移$2 \pi$的整数倍个单位，就能得到正弦曲线了。

如果只要粗略地画出图像，可以采用五点法：
找出正弦函数在$0, \dfrac{\pi}{2}, \pi, \dfrac{3 \pi}{2}, 2 \pi$的值$0, 1, 0, -1, 0$，描出这5个点，用光滑的曲线依次连接起来，就能得到正弦函数的简图。

类似地，我们可以得到余弦函数的图像，即余弦曲线。

根据诱导公式六$\cos \alpha = \sin(\dfrac{\pi}{2} + \alpha)$，可知余弦曲线实际上就是正弦曲线向左平移$\dfrac{\pi}{2}$个单位。

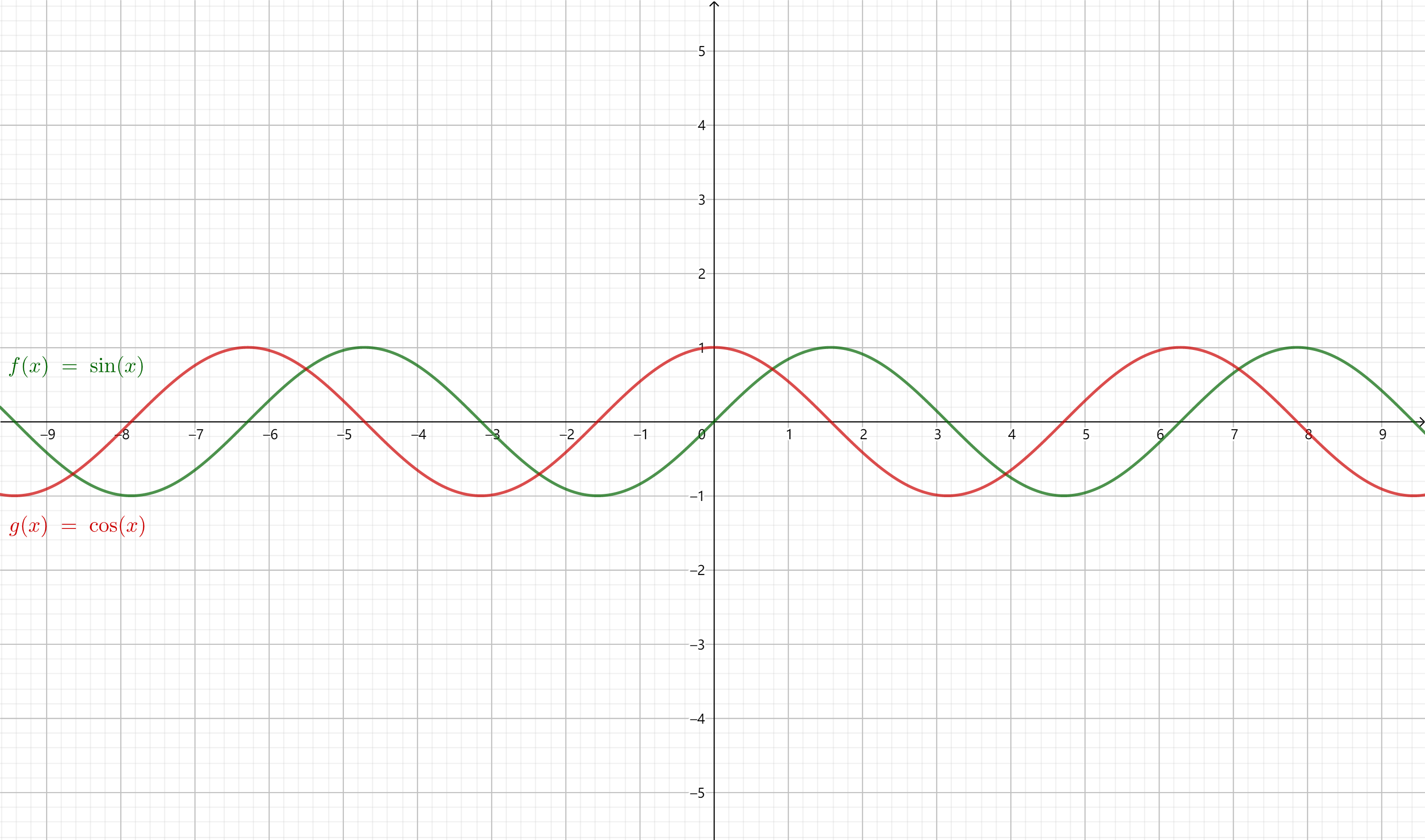
三角函数最显著的性质是周期性。
观察图像以及诱导公式一可以得出，
正弦函数和余弦函数的周期为$2 k \pi (k \in \mathbb{Z})$，最小正周期为$2 \pi$。
证明：
首先我们需要假定两个命题是正确的：一是正弦函数和余弦函数是连续的；二是连续的非常数的周期函数存在最小正周期。
设正弦函数存在最小正周期$T$，已知$2 \pi$是正弦函数的一个周期，那么存在正整数$n$使得$n T = 2 \pi$。
若$n > 2$，有$0 = \sin 0 = \sin T = \sin \dfrac{2 \pi}{n}$，显然矛盾，因此$n \le 2$。
若$n = 2$，有$1 = \sin \dfrac{\pi}{2} = \sin(\pi + \dfrac{\pi}{2}) = -1$，依然矛盾，因此$n = 1$，$T = 2 \pi$。
余弦函数的证明同理。$\Box$

由诱导公式三$\sin(-\alpha) = -\sin \alpha, \cos(-\alpha) = \cos \alpha$可得：
正弦函数是奇函数，余弦函数是偶函数。

由诱导公式二$\sin(\pi + \alpha) = -\sin \alpha$可得$\sin(\pi + \alpha)$也是奇函数，因此$(\pi, 0)$和原点一样也是正弦函数的对称中心。
由诱导公式二和六$\sin(\dfrac{\pi}{2} + \alpha) = \cos \alpha, \sin(\dfrac{3 \pi}{2} + \alpha) = -\cos \alpha$可得$\sin(\dfrac{\pi}{2} + \alpha)$和$\sin(\dfrac{3 \pi}{2} + \alpha)$都是偶函数，因此直线$x = \dfrac{\pi}{2}, x = \dfrac{3 \pi}{2}$和$y$轴一样也是正弦函数的对称轴。
根据正弦函数的周期性有：
正弦曲线以$(k \pi, 0) (k \in \mathbb{Z})$为对称中心，以直线$x = \dfrac{\pi}{2} + k \pi (k \in \mathbb{Z})$为对称轴。
同理，
余弦曲线以$(\dfrac{\pi}{2} + k \pi, 0) (k \in \mathbb{Z})$为对称中心，以直线$x = k \pi (k \in \mathbb{Z})$为对称轴。

周期性和对称性使得我们只需要研究$[0, \dfrac{\pi}{2}]$上的单调性，转化为锐角三角函数。
通过几何容易证明，正弦函数在$[0, \dfrac{\pi}{2}]$上单调递增。由对称轴$x = \dfrac{\pi}{2}$可以得到，正弦函数在$[\dfrac{\pi}{2}, \pi]$上单调递减。再通过中心对称可以得到正弦函数在长度为$2 \pi$的区间上的单调性，最后由周期性扩展到整个定义域：
正弦函数在$[2 k \pi - \dfrac{\pi}{2}, 2 k \pi + \dfrac{\pi}{2}] (k \in \mathbb{Z})$上单调递增，在$[2 k \pi + \dfrac{\pi}{2}, 2 k \pi + \dfrac{3 \pi}{2}] (k \in \mathbb{Z})$上单调递减。

由单调性可以得到，
正弦函数当且仅当$x = 2 k \pi + \dfrac{\pi}{2} (k \in \mathbb{Z})$时取得最大值$1$，当且仅当$x = 2 k \pi - \dfrac{\pi}{2} (k \in \mathbb{Z})$时取得最小值$-1$。
最值也可以通过同角三角函数关系式得到：

$$\sin^{2} \alpha \le \sin^{2} \alpha + \cos^{2} \alpha = 1 \Rightarrow |\sin \alpha| \le 1 \Rightarrow -1 \le \sin \alpha \le 1$$

等号成立当且仅当$\cos \alpha = 0$即$\alpha = k \pi + \dfrac{\pi}{2} (k \in \mathbb{Z})$。

因为余弦曲线是正弦曲线的平移，所以不难得到：
余弦函数在$[2 k \pi -\pi, 2 k \pi] (k \in \mathbb{Z})$上单调递增，在$[2 k \pi, 2 k \pi + \pi] (k \in \mathbb{Z})$上单调递减。
余弦函数当且仅当$x = 2 k \pi (k \in \mathbb{Z})$时取得最大值$1$，当且仅当$x = 2 k \pi + \pi (k \in \mathbb{Z})$时取得最小值$-1$。

正切函数

前面已经提到过，正切函数的定义域是$\{x | x \ne k \pi + \dfrac{\pi}{2}, k \in \mathbb{Z}\}$。

由诱导公式二$\tan(\pi + \alpha) = \tan \alpha$可得，$\pi$是正切函数的一个周期。事实上，
正切函数的最小正周期为$\pi$。

在单位圆上作出弧度为$x_{0}$的角，终边交单位圆于点$B$，交直线$x = 1$于点$N$。设$A(1, 0)$并过点$B$作$x$轴的垂线，垂足为$M$。那么三角形$OBM, ONA$相似，因此点$N$的纵坐标

$$y_{0} = |AN| = \dfrac{|NA|}{|OA|} = \dfrac{|BM|}{|OM|} = \tan x_{0}$$

以$x_{0}$为横坐标，$y_{0}$为纵坐标，即可得到函数图像上的点$T(x_{0}, \sin x_{0})$。
画出足够多的点并用光滑的曲线连接起来，我们就得到了正切函数的图像，即正切曲线。

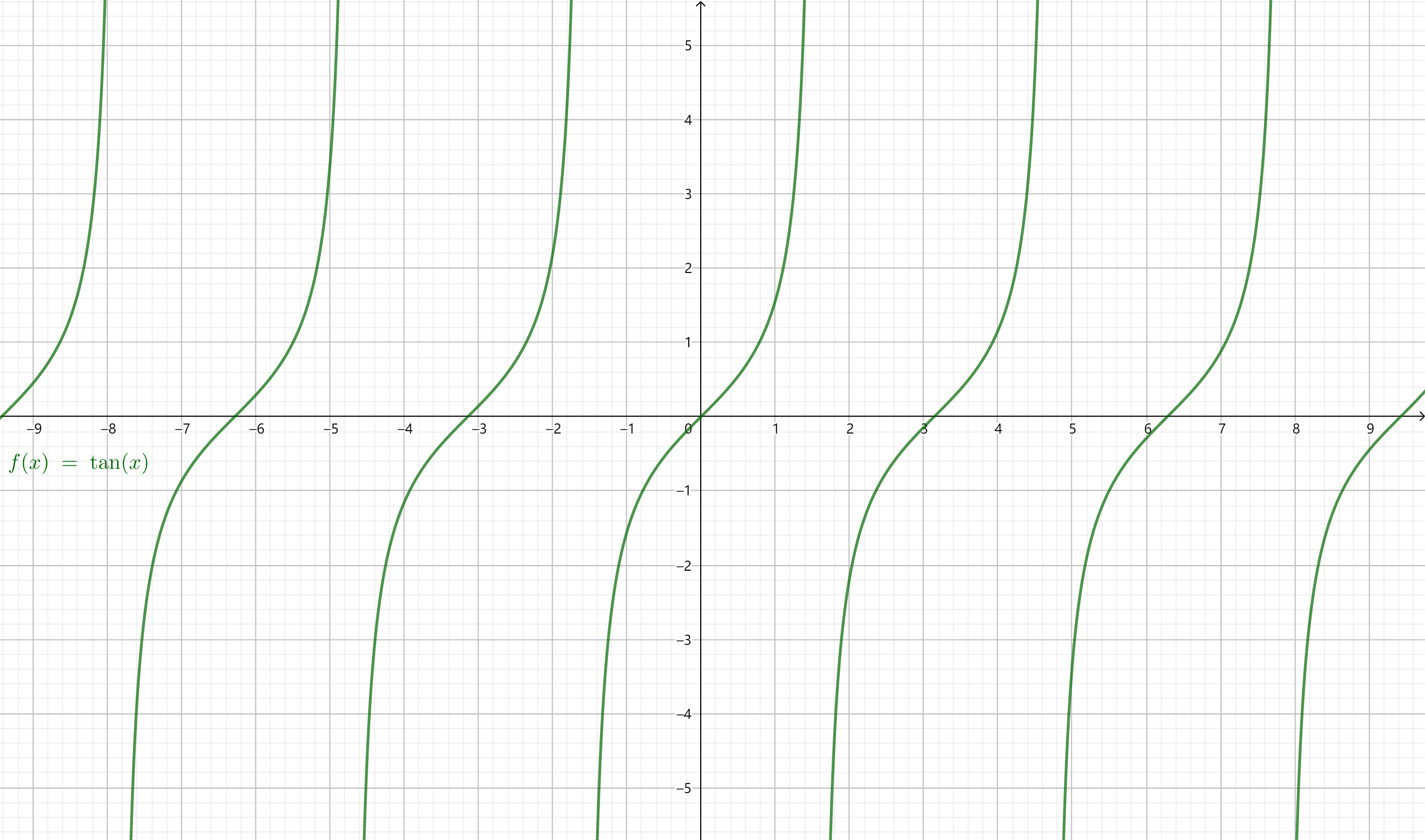
可以看出，正切函数以$(\dfrac{k \pi}{2}, 0)$为对称中心。
由诱导公式三$\tan(-\alpha) = -\tan \alpha$可得，正切函数是奇函数。

正切函数在$(k \pi - \dfrac{\pi}{2}, k \pi + \dfrac{\pi}{2}) (k \in \mathbb{Z})$上单调递增。

$$\tan x = \dfrac{\sin x}{\cos x}$$

$x$从左边趋于$\dfrac{\pi}{2}$，$\sin x$增大趋于$1$，而$\cos x$减小趋于$0$，使得$\tan x$趋于正无穷大。$x$从右边趋于$\dfrac{\pi}{2}$时则$\tan x$趋于负无穷大。
因此正切函数的值域是$\mathbb{R}$。

函数$f(x) = A \sin(\omega x + \varphi)$

三角函数常用来刻画一些物理现象，例如匀速圆周运动。
设一半径为$r$的圆形水车以角速度$\omega$匀速转动。以水车的中心为原点，一个水桶在开始转动时位于角$\varphi$的终边上，那么在旋转时间$t$后，水桶对应的角就是$\omega t + \varphi$。此时水桶的高度（纵坐标）

$$h = r \sin(\omega t + \varphi)$$

这个函数就是我们所要研究的。

函数$f(x) = A \sin(\omega x + \varphi)$有三个参数：
振幅（amplitude）$A$、圆频率（circular frequency）或角频率（angular frequency）$\omega$、初相（initial phase）$\varphi$。
它们对函数图像的影响各不一样。

首先，$f(x + \varphi)$的图像是$f(x)$平移$\varphi$个单位得到的，那么初相$\varphi$的作用就是平移；
其次，从$f(x)$变为$A f(x)$，函数值变为了原来的$A$倍，那么振幅$A$的作用就是纵向的拉伸，由此得到函数的值域为$[-A, A]$；
最后，从$f(x)$变为$f(\omega x)$，$f(\omega \cdot \dfrac{x}{\omega}) = f(x)$，函数图像上每一点$(x, f(x))$都变为了$(\dfrac{x}{\omega}, f(x))$，那么振幅$A$的作用就是横向的压缩。

因此，函数$f(x) = A \sin(\omega x + \varphi) (A > 0, \omega > 0)$的图像可以通过三步从正弦曲线变化而来：

1. 把正弦曲线平移$\varphi$个单位，左加右减；
2. 把得到的曲线上每一点横坐标都变为原来的$\dfrac{1}{\omega}$；
3. 把得到的曲线上每一点纵坐标都变为原来的$A$倍。

此外，五点法也可以画出图像：
令$z = \omega x + \varphi$，分别解方程$z = 0, \dfrac{\pi}{2}, \pi, \dfrac{3 \pi}{2}, 2 \pi$，描出这5个点$(x, A \sin x)$，用光滑的曲线依次连接起来，就能得到一个周期内的图像。

令$z = \omega x + \varphi$，则函数$f(z) = A \sin z$的最小正周期为$2 \pi$。
因为

$$z + 2 \pi = (\omega x + \varphi) + 2 \pi = \omega (x + \dfrac{2 \pi}{\omega}) + \varphi$$

所以函数$f(x) = A \sin(\omega x + \varphi) (A \ne 0, \omega \ne 0)$的最小正周期$T = \dfrac{2 \pi}{|\omega|}$。

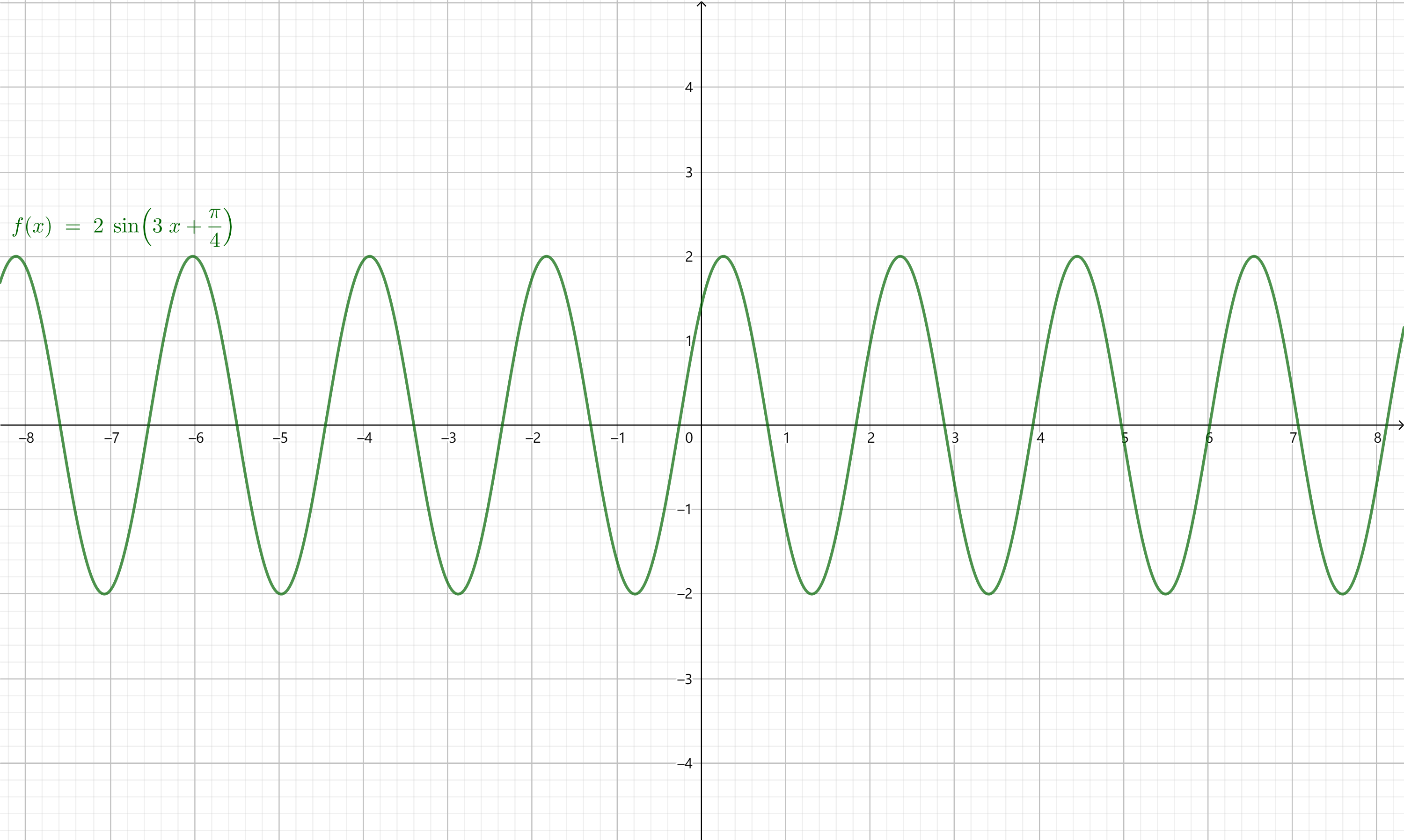
用函数$f(x) = A \sin(\omega x + \varphi) (A > 0, \omega > 0)$来刻画简谐运动，$\omega x + \varphi$实际上就是简谐运动的相位（phase），简谐运动的周期（period）$T = \dfrac{2 \pi}{\omega}$，频率（frequency）$f = \dfrac{1}{T} = \dfrac{\omega}{2 \pi}$。

反三角函数

有时候，我们需要求三角函数的反函数，例如求解方程$\sin x = a, a \in [-1, 1]$。
但是三角函数是周期函数，不是双射，没有反函数。因此先对三角函数的定义域加以限制，使其成为双射函数，这时就可以定义反三角函数（inverse trigonometric function）了。

函数$f(x) = \sin x, x \in [-\dfrac{\pi}{2}, \dfrac{\pi}{2}]$是一个双射函数，在这个区间上是增函数，从$-1$递增到$1$。这样的函数的反函数$f^{-1}(x)$称作反正弦函数（arcsine function），记作$\arcsin x$。也记作$\sin^{-1} x$，但容易与$\dfrac{1}{\sin x}$混淆。
反正弦函数的定义域是$[-1, 1]$，值域是$[-\dfrac{\pi}{2}, \dfrac{\pi}{2}]$，是一个增函数和奇函数。
反正弦函数与正弦函数对比的图像如下：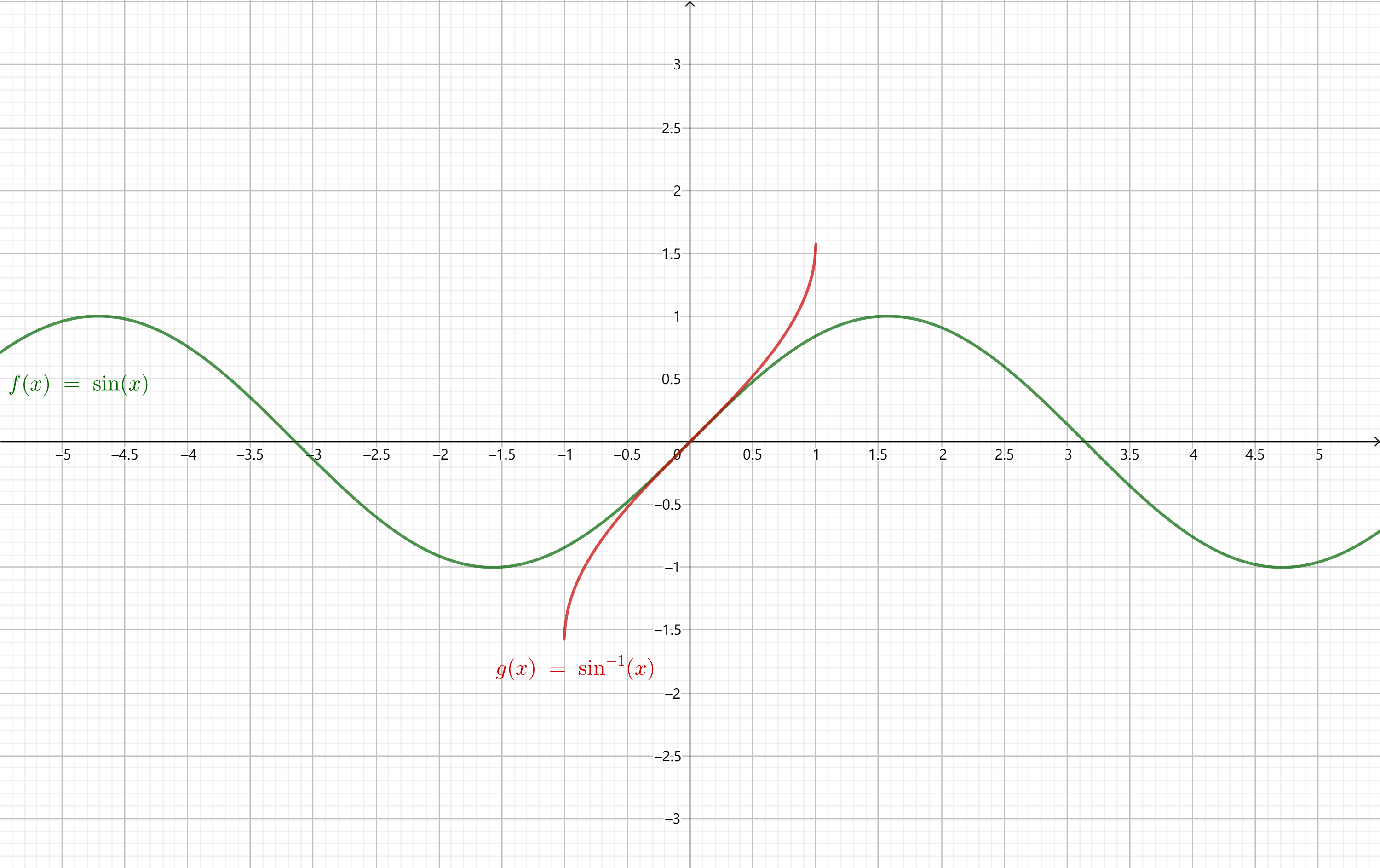

我们可以利用反正弦函数来解三角方程$\sin x = a, a \in [-1, 1]$。
若$a = 1$，则解为$x = 2 k \pi + \dfrac{\pi}{2} (k \in \mathbb{Z})$；
若$a = -1$，则解为$x = 2 k \pi - \dfrac{\pi}{2} (k \in \mathbb{Z})$；
若$-1 < a < 1$，我们先找到方程在一个周期$[-\dfrac{\pi}{2}, \dfrac{3 \pi}{2})$内的解，为$\arcsin a$和$\pi - \arcsin a$。扩展到所有周期，就得到解为$x = 2 k \pi + \arcsin a (k \in \mathbb{Z})$或$x = (2 k + 1) \pi - \arcsin a (k \in \mathbb{Z})$。
综上，$\sin x = a, a \in [-1, 1]$的解为

$$x = k \pi + (-1)^{k} \arcsin a (k \in \mathbb{Z})$$

对于余弦函数和正切函数，分别定义：
$g(x) = \cos x, x \in [0, \pi]$的反函数为反余弦函数（arccosine function），记作$\arccos x$，有时也记作$\cos^{-1} x$；
$h(x) = \tan x, x \in (-\dfrac{\pi}{2}, \dfrac{\pi}{2})$的反函数为反正切函数（arctangent function），记作$\arctan x$，有时也记作$\tan^{-1} x$。

和差角公式与二倍角公式

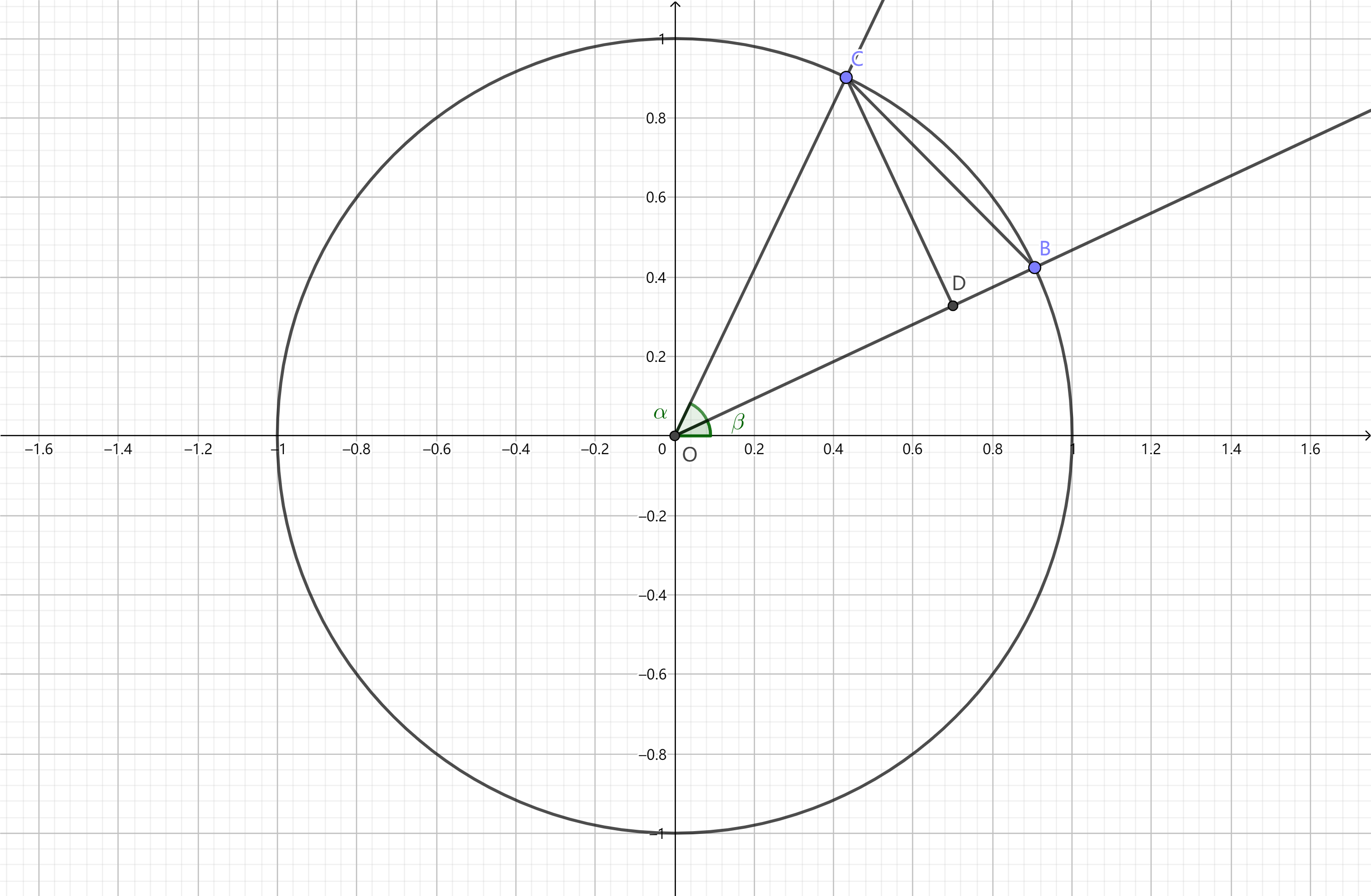
如图，设$\alpha \ne 2 k \pi + \beta (k \in \mathbb{Z})$且$\alpha > \beta$，角$\alpha, \beta$的终边分别是射线$OC, OB$。
由三角函数定义，得$B(\cos \beta, \sin \beta), C(\cos \alpha, \sin \alpha)$，所以

$$|BC|^{2} = (\cos \alpha - \cos \beta)^{2} + (\sin \alpha - \sin \beta)^{2}$$

过点$C$作$OB$的垂线，垂足为$D$，则$|CD| = |\sin(\alpha - \beta)|, |BD| = |1 - \cos(\alpha - \beta)|$。

$$|BC|^{2} = |BD|^{2} + |CD|^{2} = \sin^{2} (\alpha - \beta) + (1 - \cos(\alpha - \beta))^{2}$$

比较两式，得

$$\cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta$$

$\alpha = 2 k \pi + \beta (k \in \mathbb{Z})$时，容易证明上式仍然成立。

我们知道$\alpha + \beta = \alpha - (-\beta)$，因此利用上式和诱导公式三可以证明

$$\cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta$$

用诱导公式五或六将余弦转化为正弦，可以得到

$$\begin{align} & \sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \\ & \sin(\alpha - \beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta \end{align}$$

利用同角三角函数关系式，可以得到

$$\begin{align} & \tan(\alpha + \beta) = \dfrac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta} \\ & \tan(\alpha - \beta) = \dfrac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta} \end{align}$$

以上六个公式中，用于求任意角$\alpha, \beta$的和角$\alpha + \beta$的三角函数的三个公式，叫做和角公式；
用于求差角$\alpha - \beta$的三角函数的三个公式，叫做差角公式。

取和角公式中的$\beta = \alpha$，可以得到二倍角公式：

$$\begin{align} & \sin 2 \alpha = 2 \sin \alpha \cos \alpha \\ & \cos 2 \alpha = \cos^{2} \alpha - \sin^{2} \alpha \\ & \tan 2 \alpha = \dfrac{2 \tan \alpha}{1 - \tan^{2} \alpha} \end{align}$$

利用同角三角函数关系式又可以得到

$$\cos 2 \alpha = 1 - 2 \sin^{2} \alpha = 2 \cos^{2} \alpha - 1$$

由于

$$\begin{align} & \sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \\ & \sin(\alpha - \beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta \end{align}$$

两式相加可得到

$$\sin \alpha \cos \beta = \dfrac{\sin(\alpha + \beta) + \sin(\alpha - \beta)}{2}$$

将$\alpha = \dfrac{\theta + \varphi}{2}, \beta = \dfrac{\theta - \varphi}{2}$代入上式，则$\alpha + \beta = \theta, \alpha - \beta = \varphi$，得到

$$\sin \theta + \sin \varphi = 2 \sin \dfrac{\theta + \varphi}{2} \cos \dfrac{\theta - \varphi}{2}$$

第一个公式属于积化和差公式，第二个公式属于和差化积公式，同理可以推出带减号的以及余弦和正切的类似公式。

辅助角公式也是一个常用公式：

$$\begin{align} a \sin x + b \cos x &= \sqrt{a^{2} + b^{2}} \sin(x + \arctan \dfrac{b}{a}), a > 0 \\ &= \sqrt{a^{2} + b^{2}} \cos(x - \arctan \dfrac{b}{a}), b > 0 \end{align}$$

推导并不复杂：

$$a \sin x + b \cos x = \sqrt{a^{2} + b^{2}} (\dfrac{a}{\sqrt{a^{2} + b^{2}}} \sin x + \dfrac{b}{\sqrt{a^{2} + b^{2}}} \cos x)$$

设点$(a, b)$为角$\varphi (-\dfrac{\pi}{2} < \varphi < \dfrac{\pi}{2})$终边上的一点，则$\cos \varphi = \dfrac{a}{\sqrt{a^{2} + b^{2}}}, \sin \varphi = \dfrac{b}{\sqrt{a^{2} + b^{2}}}$。得到

$$a \sin x + b \cos x = \sqrt{a^{2} + b^{2}} (\sin x \cos \varphi + \cos x \sin \varphi)$$

即

$$a \sin x + b \cos x = \sqrt{a^{2} + b^{2}} \sin(x + \varphi)$$

其中$\varphi = \arctan \dfrac{b}{a}, a > 0$。余弦形式的证明同理。
如果$a, b$取负数，则辅助角$\varphi = \arctan \dfrac{b}{a} \pm \pi$，正弦或余弦前要相应地添上负号。$\Box$

解三角形

给出三角函数的一些边和角，求出符合条件的三角形，这种问题叫做解三角形。
以下介绍一些解三角形中重要的定理：

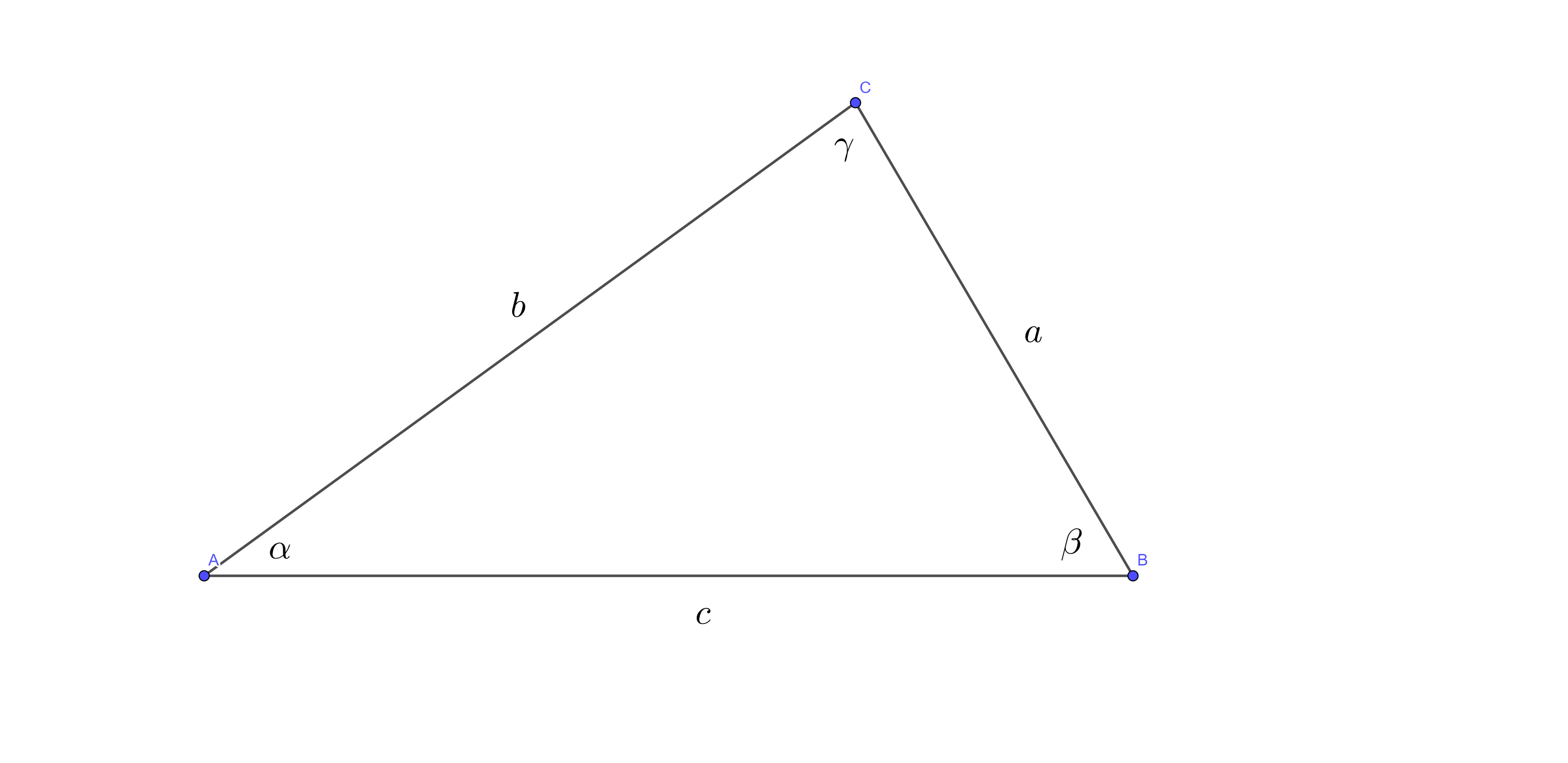
如图，在$\triangle ABC$中，$BC = a, AC = b, AB = c$，$r$为$\triangle ABC$的外接圆半径。
正弦定理（law of sines）：

$$\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2r$$

几何证明见这里。

余弦定理（law of cosines）：

$$\begin{align} & c^{2} = a^{2} + b^{2} - 2ab \cos C \\ & b^{2} = c^{2} + a^{2} - 2ca \cos B \\ & a^{2} = b^{2} + c^{2} - 2bc \cos A \end{align}$$

几何证明见这里。
以下给出代数证明：
根据正弦定理，$c = 2 r \sin C, a = 2 r \sin A, b = 2 r \sin B$，
代入$c^{2} = a^{2} + b^{2} - 2ab \cos C$，约去$4 r^{2}$得

$$\sin^{2} C = \sin^{2} A + \sin^{2} B - 2 \sin A \sin B \cos C$$

右边使用二倍角公式与积化和差、和差化积公式化简：

$$\begin{align} & \quad \sin^{2} A + \sin^{2} B - 2 \sin A \sin B \cos C \\ &= 1 - \dfrac{1}{2} (\cos 2 A + \cos 2 B) - (\cos(A - B) - \cos(A + B)) \cos C \\ &= 1 - \cos(A - B) \cos(A + B) - \cos(A - B) \cos C - \cos^{2} C \\ &= 1 - \cos^{2} C \\ &= \sin^{2} C \end{align}$$

其中由于$A + B + C = \pi$，得$\cos(A + B) = -\cos C$。$\Box$

射影定理：

$$\begin{align} & a = b \cos C + c \cos B \\ & b = c \cos A + a \cos C \\ & c = a \cos B + b \cos A \end{align}$$

几何证明见这里。

附：欧拉公式与三角函数

欧拉公式（Euler’s formula）有：

$$\mathrm{e}^{\mathrm{i} \theta} = \cos \theta + \mathrm{i} \sin \theta$$

这个公式涉及到了虚数，不过暂时只要知道虚数单位$\mathrm{i}^2 = -1$就好了。

由

$$\mathrm{e}^{\mathrm{i} (\alpha + \beta)} = \mathrm{e}^{\mathrm{i} \alpha} \cdot \mathrm{e}^{\mathrm{i} \beta}$$

得

$$\cos(\alpha + \beta) + \mathrm{i} \sin(\alpha + \beta) = (\cos \alpha + \mathrm{i} \sin \alpha) (\cos \beta + \mathrm{i} \sin \beta)$$

将实部与实部对应，虚部与虚部对应，整理可得前面的和角公式：

$$\begin{align} & \cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta \\ & \sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \end{align}$$

令$\beta = \alpha$，可得前面的二倍角公式。

令$\beta = -\beta$，可得前面的差角公式：

$$\begin{align} & \cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \\ & \sin(\alpha - \beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta \end{align}$$

再通过对和角公式与差角公式作和或差，可得积化和差公式；
令$\alpha = \dfrac{\theta + \varphi}{2}, \beta = \dfrac{\theta - \varphi}{2}$，代入积化和差公式，可得和差化积公式。