学习笔记·逻辑与集合
逻辑
谓词逻辑
谓词（predicate）是表示性质或关系的词，通常用大写字母\(P, Q,
R\)等表示，而谓词刻画的对象称为主词（subject）。
例如，用\(P\)表示考了100分，\(x\)表示小刚，那么命题小刚考了100分可以记作\(P(x)\)，其中\(P\)就是谓词，\(x\)就是主词。
谓词和主词构成了原子命题，即不可再分的简单命题。
量词
有时候，我们需要对主词限定范围，进行量化。表示量化的词称之为量词（quantifier）。
最基本的两种量词是全称量词（universal
quantifier）和存在量词（existential
quantifier）。
全称量词符号为\(\forall\)，用于表示任意这样的词。
例如所有小朋友\(x\)都考了100分，可以表示为\(\forall x, P(x)\)。
存在量词符号为\(\exists\)，也称特称量词（particular
quantifier），用于表示存在这样的词。
例如至少有一个小朋友\(x\)考了100分，可以表示为\(\exists x, P(x)\)。
命题逻辑
命题（proposition）指一个陈述句所表达的判断，不涉及谓词时，我们通常用一个字母来表示命题，如\(p, q, r\)等。一般我们所指的命题非真（true）即假（false），这里的真和假表示的就是命题的真值（truth value）。
逻辑联结词
命题之间可以用逻辑联结词（logical connective）连接起来，构成复合命题。
与（合取，conjunction）和或（析取，disjunction）是最常见的两个联结词，一般用符号\(\land\)和\(\lor\)表示。（不是非法符号！）
例如，用\(p\)表示小刚考了100分，\(q\)表示小强考了100分。\(p \land q\)表示他们都考了100分，而\(p \lor q\)表示他们之中有人考了100分。
我们可以用真值表（truth table）来计算复合命题的真值：（T表示真，F表示假）
| \(p\) | \(q\) | \(p \land q\) |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
| \(p\) | \(q\) | \(p \lor q\) |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
容易看出，\(p, q\)同时为真时\(p \land q\)为真，而\(p, q\)只要有一为真时\(p \lor q\)为真。
与和或满足：
- 交换律：\(p \land q = q
\land p\)
\(p \lor q = p \lor q\) - 结合律：\((p \land q)
\land r = p \land (q \land r)\)
\((p \lor q) \lor r = p \lor (q \lor r)\) - 分配律：\(p \land (q \lor
r) = (p \land q) \lor (p \land r)\)
\(p \lor (q \land r) = (p \lor q) \land (p \lor r)\) - 幂等律：\(p \land p =
p\)
\(p \lor p = p\)
非（否定，negation）用于对命题进行否定，符号为\(\lnot\)。
非的真值表如下：
| \(p\) | \(\lnot p\) |
|---|---|
| T | F |
| F | T |
不难证明： \[ \lnot (p \land q) = \lnot p \lor \lnot q \\ \lnot (p \lor q) = \lnot p \land \lnot q \] 即反演律，也称德·摩根定律（De Morgan’s laws）。
此外，条件联结词也在数学证明中被大量用到，符号为\(\to\)，也称蕴涵（implication），但在具体的数学推理中一般使用\(\Rightarrow\)。条件联结词可以写成若\(p\)，则\(q\)的形式，其中\(p\)称为前件（antecedent），\(q\)称为后件（consequent）。
\(p \to q\)等价于\(\lnot p \lor
q\)，由此可以计算出蕴涵的真值表：
| \(p\) | \(q\) | \(p \to q\) |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
若命题\(p \to q\)为真，则称\(p\)为\(q\)的充分条件（sufficient condition），\(q\)为\(p\)的必要条件（necessary condition）。
对于命题\(p \to
q\)，其否命题为\(\lnot
p \to \lnot q\)，逆命题为\(q \to p\)，逆否命题为\(\lnot q \to \lnot
p\)。其中原命题与其逆否命题是等价的，证明如下：
由定义，\(\lnot q \to \lnot p = \lnot (\lnot
q) \lor \lnot p = \lnot p \lor q = p \to q\)。\(\Box\)
双条件联结词，即等价（equivalence），符号为\(\leftrightarrow\)或\(\Leftrightarrow\)，也称当且仅当（if
and only if, iff）。
\(p \leftrightarrow q\)表示\((p \to q) \land (q \to p)\)，此时\(p\)与\(q\)互为充要条件（sufficient and
necessary condition）。
双条件联结词可以写成当且仅当\(p\)，则\(q\)的形式，英文直译导致其并不符合汉语语法。一般当且仅当也用于描述两者互为充要条件。
双条件联结词的真值表：
| \(p\) | \(q\) | \(p \leftrightarrow q\) |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
根据复合命题在真值表最后一列的真值情况，我们将其分为三类：
- 永真式或重言式（tautology）：最后一列全是T，符号为\(\top\)。如\(p \lor \lnot p\)与\(p \to p\)等。
- 矛盾式（contradiction）：最后一列全是F，符号为\(\bot\)。如\(p \land \lnot p\)。
- 或然式（contingency）：最后一列既存在T也存在F。
全称命题与存在命题
设所有的元素为\(x_{1}, \cdots, x_{n}\)，那么对于全称命题\(\forall x, P(x)\)，实际上表示的是\(P(x_{1}) \land P(x_{2}) \land \cdots \land P(x_{n})\)，即这些命题中每个都是真的。因此不难得出全称命题的否定： \[\lnot (\forall x, P(x)) = \exists x, \lnot P(x)\]
同样，存在命题\(\exists x,
P(x)\)表示\(P(x_{1}) \lor P(x_{2}) \lor
\cdots \lor P(x_{n})\)，即至少有一个是真的。
那么 \[\lnot (\exists x, P(x)) = \forall x,
\lnot P(x)\] 这样，只要证明\(\forall x,
\lnot P(x) \Rightarrow \bot\)，就能证明原命题了。
集合
集合（set）是一个或多个对象所构成的整体，这些构成的集合的对象称为元素（element）。
集合通常用大写字母如\(A, B,
C\)等来表示，而元素通常用小写字母如\(a,
b, c\)等表示。
如果元素\(x\)在集合\(A\)内，我们称\(x\)属于\(A\)，记作\(x \in
A\)；
否则，\(x\)不属于\(A\)，记作\(x
\notin A\)。
若两个集合\(A,
B\)中的元素完全一样，即\(x \in A
\Leftrightarrow x \in B\)，则二者相等，记作\(A = B\)。
集合可以用在大括号中列举其元素的方式表示，即列举法：
\[A = \{1, 2, 3, 4, 5\}\]
对于元素较多或具有无限元素的集合，如果具有明显的规律，可以使用省略号\(\cdots\)。
例如前100个正整数： \[B = \{1, 2, \cdots,
100\}\] 自然数集： \[\mathbb{N} = \{0,
1, 2, \cdots\}\]
集合也可以通过文字或数学符号来表示，即描述法。
例如下面的集合表示\(1\)到\(5\)之间的整数： \[C = \{x \in \mathbb{Z} | 1 \le x \le 5\}\]
显然，集合\(A = C\)。
集合具有以下三个性质：
- 无序性：集合中的元素是无序的，可以任意排列
- 互异性：集合中任意两个元素都不相同，每个元素只能出现一次
- 确定性：对于一个集合，一个元素属于或不属于该集合是确定的，不能模棱两可
集合间的关系
若\(\forall x \in A, x \in
B\)，则称\(A\)是\(B\)的子集（subset），\(B\)是\(A\)的超集（superset），记作\(A \subseteq B\)或\(B \supseteq A\)，也称\(A\)包含于\(B\)或\(B\)包含\(A\)。
若\(A \subseteq B \land A \ne
B\)，即\((\forall x \in A, x \in B)
\land (\exists x \in B, x \notin A)\)，则称\(A\)是\(B\)的真子集（proper
subset），\(B\)是\(A\)的真超集（proper
superset），记作\(A \subsetneqq
B\)（\(A \subset B\)）或\(B \supsetneqq A\)（\(B \supset A\)），也称\(A\)真包含于\(B\)或\(B\)真包含\(A\)。
集合也可以通过Venn图（维恩图/文氏图，Venn
diagram）形象地表示出来。
例如下图就表示\(A\)是\(B\)的子集：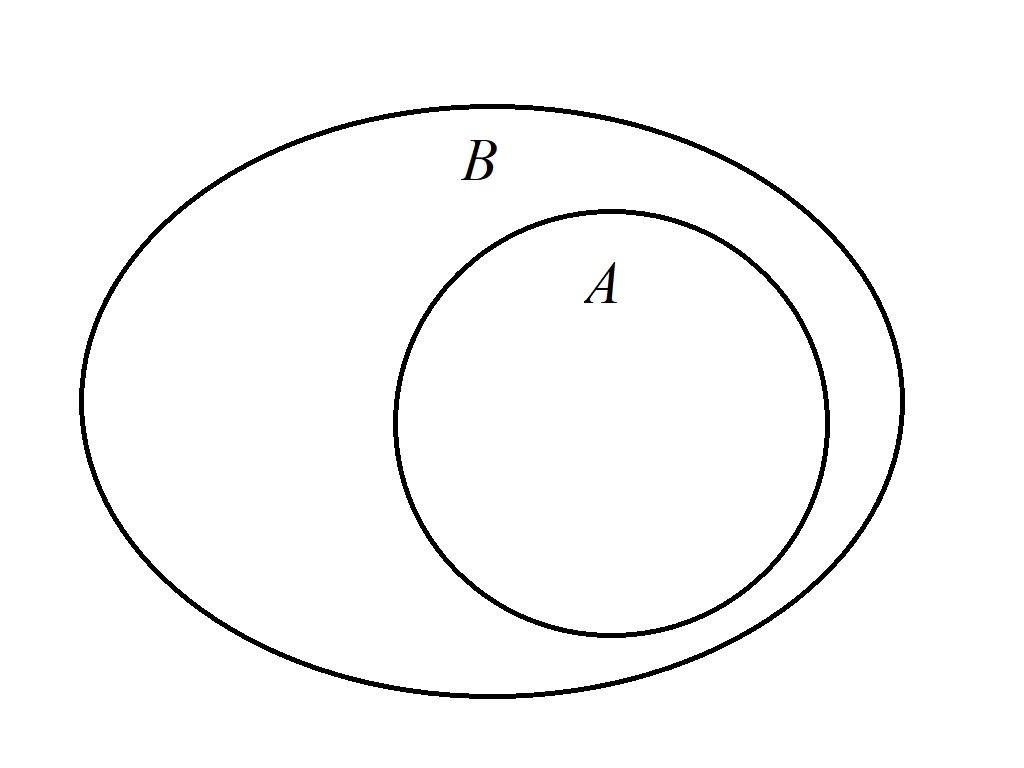 
包含关系具有
- 自反性：\(A \subseteq A\)
- 反对称性：\(A \subseteq B \land B \subseteq A \Leftrightarrow A = B\)
- 传递性：\(A \subseteq B \land B \subseteq C \Rightarrow A \subseteq C\)
真包含关系同样具有传递性。
不含任何元素的集合被称为空集（empty
set），符号为\(\varnothing\)或\(\emptyset\)。
空集有基本性质： \[\forall A, \varnothing
\subseteq A\] 这是一个可证明的定理，证明如下：
证明\(\varnothing \subseteq
A\)只要证明\(x \in \varnothing
\Rightarrow x \in A\)，其逆否命题为\(x
\notin A \Rightarrow x \notin
\varnothing\)。根据空集的定义以及蕴涵的真值表，这是真的。\(\Box\)
由这个性质不难得出： \[\forall A \ne
\varnothing, \varnothing \subsetneqq A\]
特殊集合
不同的数集通常有专门的符号表示：
\(\mathbb{N}\)表示自然数集，\(\mathbb{N}^{\ast}\)表示正整数集，\(\mathbb{Z}\)表示整数集，\(\mathbb{Q}\)表示有理数集，\(\mathbb{R}\)表示实数集，\(\mathbb{C}\)表示复数集。
\[\mathbb{N}^{\ast} \subseteq \mathbb{N}
\subseteq \mathbb{Z} \subseteq \mathbb{Q} \subseteq \mathbb{R} \subseteq
\mathbb{C}\]
此外，还有一种特殊的实数集称为区间（interval），有时用字母\(I\)表示：（\(a, b
\in \mathbb{R}\)且\(a < b\)）
\[
\begin{align}
[a, b] &= \{x \in \mathbb{R} | a \le x \le b\} \\
(a, b) &= \{x \in \mathbb{R} | a < x < b\} \\
[a, b) &= \{x \in \mathbb{R} | a \le x < b\} \\
(a, b] &= \{x \in \mathbb{R} | a < x \le b\}
\end{align}
\]
以上区间分别是闭区间、开区间、左闭右开区间和左开右闭区间。这些都是有界区间。
\(a\)和\(b\)为区间的端点，区间的长度为\(b - a\)，中点为\(\dfrac{a + b}{2}\)。
用符号\(+\infty\)和\(-\infty\)表示正无穷大和负无穷大：
\[
\begin{align}
[a, +\infty) &= \{x \in \mathbb{R} | x \ge a\} \\
(a, +\infty) &= \{x \in \mathbb{R} | x > a\} \\
(-\infty, b] &= \{x \in \mathbb{R} | x \le b\} \\
(-\infty, b) &= \{x \in \mathbb{R} | x < b\}
\end{align}
\] 特殊地，\((-\infty, +\infty) =
\mathbb{R}\)。
含有符号\(\infty\)的区间称为无界区间。
集合的运算
对于两个集合\(A,
B\)，其并集（union）定义为： \[A \cup B = \{x | x \in A \lor x \in B\}\]
即两个集合中的所有元素构成的集合。 
容易得到， \[A \cup B = B \Leftrightarrow A \subseteq B\]
对于两个集合\(A,
B\)，其交集（intersection）定义为： \[A \cap B = \{x | x \in A \land x \in B\}\]
即两个集合共同拥有的元素构成的集合。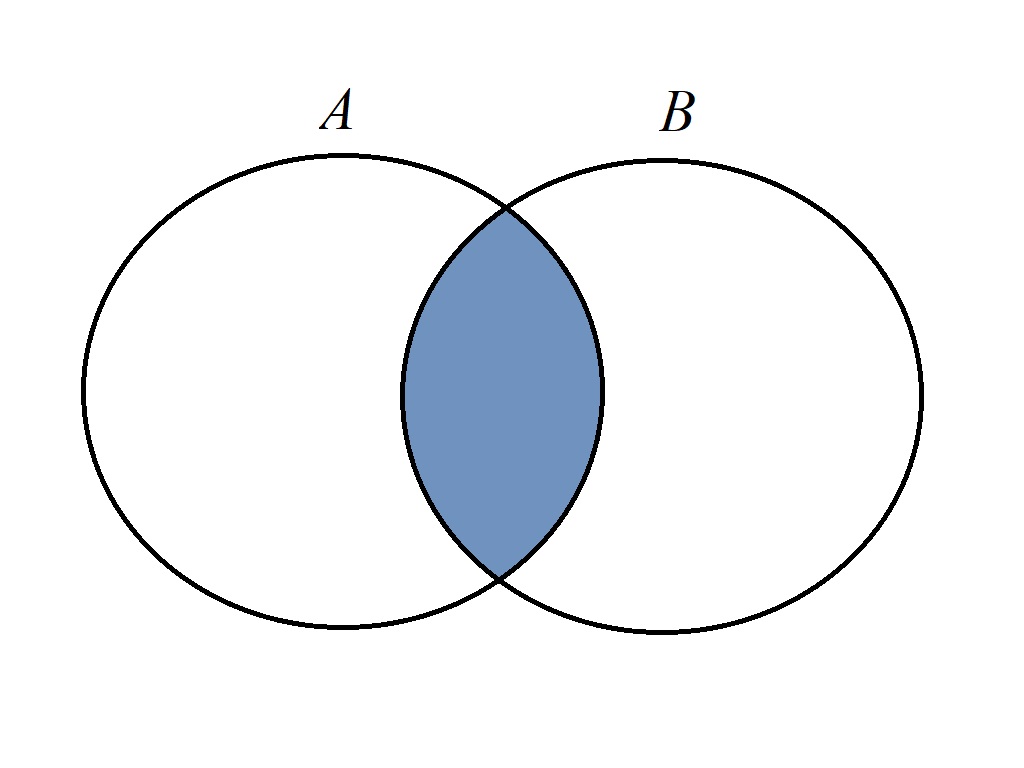 
\[A \cap B = A \Leftrightarrow A \subseteq B\]
与逻辑与和或运算类似，交集和并集也具有以下性质：
- 交换律：\(A \cap B = B
\cap A\)
\(A \cup B = B \cup A\) - 结合律：\((A \cap B) \cap
C = A \cap (B \cap C)\)
\((A \cup B) \cup C = A \cup (B \cup C)\) - 分配律：\(A \cap (B \cup
C) = (A \cap B) \cup (A \cap C)\)
\(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\) - 幂等律：\(A \cap A =
A\)
\(A \cup A = A\)
对于空集\(\varnothing\)，交集和并集还满足： \[ A \cap \varnothing = \varnothing \\ A \cup \varnothing = A \]
对于两个集合\(A, B\)，\(A\)在\(B\)中的差集（set
difference）或相对补集（relative
complement）定义为： \[B \setminus A
= \{x \in B | x \notin A\}\] \(B
\setminus A\)也记作\(B - A\)。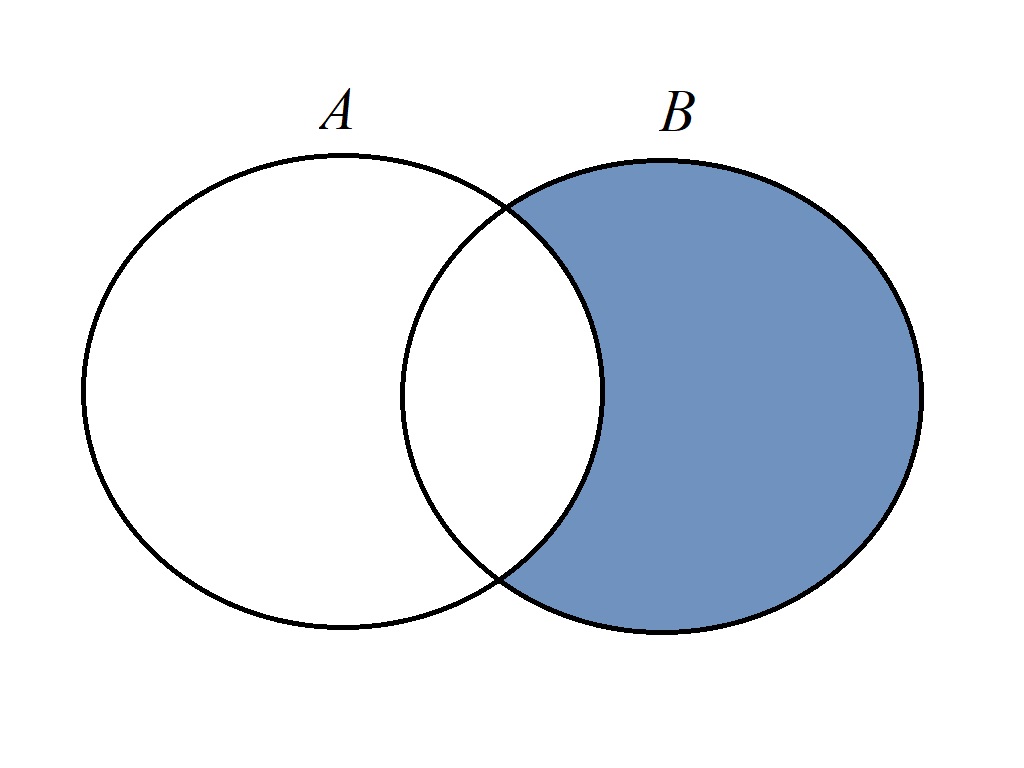
补集（complement）是一种特殊的差集，有时也称绝对补集（absolute
complement）。
在研究问题时，所有的研究对象构成的集合被称为全集（universe）。对于全集\(U\)的子集\(A\)，其补集定义为： \[\complement_{U}A = U - A = \{x \in U | x \notin
A\}\] 在不产生歧义的情况下，\(\complement_{U}A\)也可以表示为\(A^{C}\)。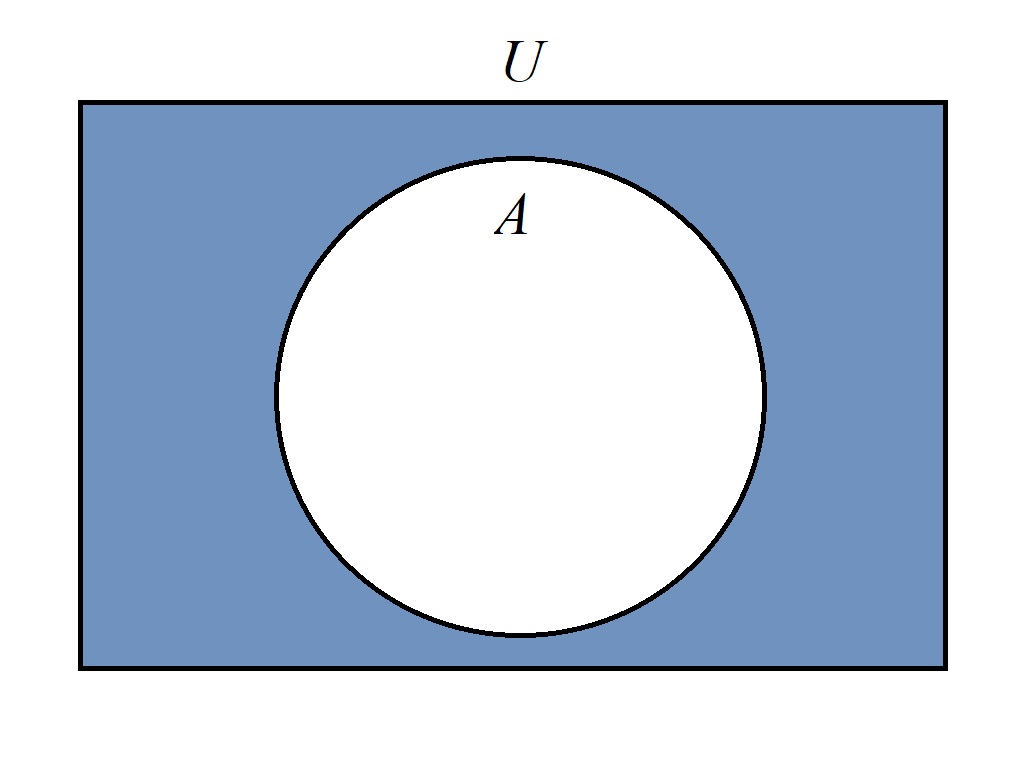 
\[A - B = \varnothing \Leftrightarrow \complement_{U}B \subseteq \complement_{U}A \Leftrightarrow A \subseteq B\]
由前面的\(\lnot (p \land q) = \lnot p \lor \lnot q, \lnot (p \lor q) = \lnot p \land \lnot q\)可以推出反演律/德·摩根定律： \[ \complement_{U}(A \cap B) = \complement_{U}A \cup \complement_{U}B \\ \complement_{U}(A \cup B) = \complement_{U}A \cap \complement_{U}B \]
对于两个集合\(A,
B\)，其对称差（symmetric difference）定义为：
\[A \bigtriangleup B = (A - B) \cup (B -
A)\] 或 \[A \bigtriangleup B = (A \cup
B) - (A \cap B)\] 
对于两个集合\(A, B\)，其笛卡尔积（Cartesian product）或直积定义为： \[A \times B = \{(a, b) | a \in A \land b \in B\}\] 例如，集合\(A\)是13个元素的点数集合\(\{A, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K\}\)，\(B\)是4个元素的花色集合\(\{\clubsuit, \diamondsuit, \heartsuit, \spadesuit\}\)，那么\(A \times B\)就是52个元素的一副标准扑克牌的集合\(\{(A, \clubsuit), (A, \diamondsuit), \cdots, (K, \heartsuit), (K, \spadesuit)\}\)。注意，笛卡尔积不满足交换律，这个集合与\(B \times A\)得到的\(\{(\clubsuit, A), (\diamondsuit, A), \cdots, (\heartsuit, K), (\spadesuit, K)\}\)是完全不同的，甚至不相交。
集合的势
如果要计算一个集合中的元素个数，我们可以用势（cardinality）或基数（cardinal
number）的概念表示。
集合\(A\)的势或基数记作\(|A|\)或\(\mathrm{card}(A)\)。
势和基数一般是同义词。有时候前者仅用于描述无限集的大小而后者用于描述有限集，但通常不加区分。本章一律使用势来表示集合的大小。
有限集合的势
顾名思义，有限集合（finite
set）就是指元素个数有限的集合。
严格定义需要用到映射：若存在自然数\(n\)以及双射\(f: A
\to \{1, 2, \cdots, n\}\)，则\(A\)为有限集合。
有限集合的势就是其元素个数\(n\)。例如集合\(A
= \{-3, 0, 2, 7, 9\}\)，则\(|A| =
5\)。
容斥原理（inclusion–exclusion
principle）是组合计数（enumerative
combinatorics）中的基本原理之一，表达为 \[|A \cup B| = |A| + |B| - |A \cap B|\]
从Venn图上可以很直观地理解这个原理。
容斥原理还可以推广到三个乃至更多集合之间： \[|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B|
- |A \cap C| - |B \cap C| + |A \cap B \cap C|\]
可以理解为三个集合相交的部分计算了三次，减去所有两两相交的部分多减了一次，因此加回三者相交的部分。
对于更多的集合，先将单个集合的势加起来，然后减去所有两个集合相交的部分，再加回所有三个集合相交的部分，再减去所有四个集合相交的部分，依此类推。
集合的幂集（power
set），定义为该集合全部子集构成的集合。
对于集合\(S\)，其幂集\(\mathcal{P}(S)\)可以表示为： \[\mathcal{P}(S) = \{x | x \subseteq S\}\]
\(S\)的幂集也可以记作\(2^{S}\)。
例如一集合\(S = \{a, b,
c\}\)，那么\(S\)的幂集 \[\mathcal{P}(S) = \{\varnothing, \{a\}, \{b\},
\{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\}\}\]
幂集的实质就是考虑集合\(S\)中每一个元素选或不选，每一种选择构成一个集合，因此可以得出
\[|S| = n, |\mathcal{P}(S)| =
2^{n}\]
无限集合的势
不是有限集合的集合就是无限集合（infinite
set）。
若两个集合\(A, B\)之间存在双射\(f: A \to
B\)，则称这两个集合等势。
对于自然数集\(\mathbb{N}\)，我们定义它的势为\(\aleph_{0}\)，读作阿列夫零（aleph-naught）。
若集合\(A\)与\(\mathbb{N}\)等势，则称\(A\)为可数集（countable
set），\(|A| =
\aleph_{0}\)。
可数集和有限集统称至多可数集合（at most countable
set）。
设集合\(S\)，若存在单射\(f: S \to \mathbb{N}\)或满射\(g: \mathbb{N} \to S\)，则\(S\)为至多可数集合。
至多可数集合的子集都是至多可数集合，可以通过将第\(n\)个元素映射到自然数\(n\)上证明。
类似地，我们也能证明\(\mathbb{Z}\)和\(\mathbb{Q}\)都是可数集，即使看上去它们要比\(\mathbb{N}\)大。
可数个至多可数集合的并集是至多可数集合。
证明：
设可数集\(A, B, C,
\cdots\)，它们的元素分别为\(A =
\{a_{0}, a_{1}, a_{2}, \cdots\}, B = \{b_{0}, b_{1}, b_{2}, \cdots\},
\cdots\)。将这些集合的元素排列为 \[
\begin{align}
&a_{0} \quad b_{0} \quad c_{0} \quad \cdots \\
&a_{1} \quad b_{1} \quad c_{1} \quad \cdots \\
&a_{2} \quad b_{2} \quad c_{2} \quad \cdots \\
&\ \vdots \quad\ \ \vdots \quad\ \ \ \vdots
\end{align}
\] 将这些元素按对角线与下面的自然数一一对应： \[
\begin{align}
&0 \quad 2 \quad 5 \quad \cdots \\
&1 \quad 4 \quad 8 \quad \cdots \\
&3 \quad 7 \quad 12 \quad \cdots \\
&\vdots \quad\ \vdots \quad\ \vdots
\end{align}
\] 即可得这些集合的并集为可数集。\(\Box\)
无限集合中不是可数集的就是不可数集（uncountable
set），例如\(\mathbb{R}\)。
不可数集的势大于可数集。
记\(|\mathbb{R}| = \aleph_{1}\)，读作阿列夫一（aleph-one）。
我们知道，\(\aleph_{0} <
\aleph_{1}\)，那么这两者之间是否还有其它基数？
德国数学家康托尔（Georg
Cantor，1845—1918）对这个问题给出了否定的答案，提出了连续统假设（continuum
hypothesis, CH），表述为：
不存在一个集合，其势大于\(\mathbb{N}\)而小于\(\mathbb{R}\)。
连续统假设等价于以下等式： \[2^{\aleph_{0}} =
\aleph_{1}\]
这个猜想后来被证明独立于我们常用的这个公理系统之外，即不可被证明或证伪。
附：大型运算符
常见的大型运算符有 \[\sum, \prod, \bigcup, \bigcap, \bigvee, \bigwedge\]
给定一些数\(a_{1}, a_{2}, a_{3}, \cdots,
a_{n}\)，它们的和\(a_{1} + a_{2} +
a_{3} + \cdots + a_{n}\)可以写作 \[\sum\limits_{i=1}^{n} a_{i}\]
其中下标\(i = 1\)表示\(i\)的初始值为\(1\)，上标\(n\)表示\(i\)从初始值\(1\)遍历到\(n\)。上式的意思即\(a_{i}\)的和，\(i\)从\(1\)到\(n\)。
特别注意，如果下标大于上标，式子的值一般定义为\(0\)。
例如， \[\sum\limits_{i=3}^{6} i^{2} = 3^{2} + 4^{2} + 5^{2} + 6^{2} = 86\]
在不造成歧义的情况下，\(\sum\limits_{i=1}^{n}\)可以直接简写成\(\sum\limits\)，例如， \[\sum\limits a_{i} = \sum\limits_{i=1}^{n} a_{i}\]
同理，
\(\prod\limits_{i=1}^{n}
a_{i}\)表示\(a_{1}, a_{2}, \cdots,
a_{n}\)的乘积；
\(\bigcap\limits_{i=1}^{n}
A_{i}\)表示集合\(A_{1}, A_{2}, \cdots,
A_{n}\)的交集；
\(\bigvee\limits_{i=1}^{n}
p_{i}\)表示对命题\(p_{1}, p_{2},
\cdots, p_{n}\)取或。
此外，如果我们要限定下标的值，例如下标\(i\)属于非负整数集合\(A\)，可以写作 \[\sum\limits_{i \in A} a_{i}\] 如果集合\(A\)可以用描述法写成\(A = \{i | p(i)\}\)，那么可以写作 \[\sum\limits_{p(i)} a_{i}\] 如果下标要排除某个数\(m\)，可以写作 \[\sum\limits_{i \ne m} a_{i}\]
如果要使用多个大型运算符如\(\sum\limits_{i} \sum\limits_{j}\)，可以简写作 \[\sum\limits_{i, j}\]
求和符号比较特殊，它具有线性性： \[ \begin{align} & \sum\limits (a_{i} + b_{i}) = \sum\limits a_{i} + \sum\limits b_{i} \\ & \sum\limits k a_{i} = k \sum\limits a_{i} \end{align} \]
连乘符号也有类似的性质： \[ \begin{align} & \prod\limits a_{i} b_{i} = \prod\limits a_{i} \prod\limits b_{i} \\ & (\prod\limits a_{i})^{k} = \prod\limits a_{i}^{k} \end{align} \]