语言学

语言学（linguistics），顾名思义，是研究语言的科学。
中国、印度和希腊与罗马在古代就出现了语文学（filology），这是对语言系统研究的开始。例如，中国的语文学研究围绕汉字进行，称为「小学」，包括文字学、音韵学、训诂学。语文学和语言学的区别在于，语文学研究的直接目的是解读古典文献，而非探究语言本身的规律，其关注的重点是古典文献所反映的古代思想和文化。

这里采用的是欧陆西班牙语（español europeo）的语法体系，但也会提及美洲西班牙语（español americano）中的不同语法。

语法结构

导数

如果函数\(f(x)\)在\(x_{0}\)的一个邻域\((x_{0} - \delta, x_{0} + \delta)\)有定义，且极限\(\lim\limits_{\Delta x \to 0} \dfrac{f(x_{0} + \Delta x) - f(x_{0})}{\Delta x}\)存在，那么称这个极限为\(f\)在\(x_{0}\)的导数（derivative），记作\(f'(x_{0})\)或\(\dfrac{\mathrm{d} f}{\mathrm{d} x}(x_{0})\)；若设\(y = f(x)\)，则还可以记作\(\left. y' \right|_{x=x_{0}}\)或\(\left. \dfrac{\mathrm{d} y}{\mathrm{d} x} \right|_{x=x_{0}}\)。此时称\(f\)在\(x_{0}\)可导（differentiable）。
如果函数\(f(x)\)在\(x_{0}\)的一个左邻域\((x_{0} - \delta, x_{0}]\)有定义，且极限\(\lim\limits_{\Delta x \to 0^{-}} \dfrac{f(x_{0} + \Delta x) - f(x_{0})}{\Delta x}\)存在，那么称这个极限为\(f\)在\(x_{0}\)的左导数（left derivative），记作\(f'_{-}(x_{0})\)；如果函数\(f(x)\)在\(x_{0}\)的一个右邻域\([x_{0}, x_{0} + \delta)\)有定义，且极限\(\lim\limits_{\Delta x \to 0^{+}} \dfrac{f(x_{0} + \Delta x) - f(x_{0})}{\Delta x}\)存在，那么称这个极限为\(f\)在\(x_{0}\)的右导数（right derivative），记作\(f'_{+}(x_{0})\)。
显然，函数在\(x_{0}\)可导的充要条件是：它在\(x_{0}\)的左导数和右导数存在且相等。

修改最新Commit

如果只要修改最新提交，可以直接使用命令git commit --amend，在文本编辑器中编辑并保存。如果提交已经推送，需要用git push --force强制推送。

前言

日本近代史始于1868年明治维新，终于1945年第二次世界大战战败，可以分为明治时代（1868—1912）、大正时代（1912—1926）和昭和时代（1926—1945）。
第一章“明治维新”介绍了明治维新（1868），第二章“明治前期的内政外交”介绍了明治前期（1868—1889），第三章“军事封建帝国主义的形成”介绍了明治后期（1889—1912），第四章“明治文化”介绍了明治时代的文化；
第五章“大正时代”介绍了大正时代（1912—1926），第六章“日本法西斯主义的形成”介绍了二战前的日本（1926—1937），第七章“大正浪漫与昭和摩登”介绍了二战前日本的文化，第八章“侵华战争”介绍了太平洋战争前的日本侵华战争（1937—1941），第九章“太平洋战争”介绍了太平洋战争（1941—1945）。

前言

相较于传统的Python打包工具pyinstaller，Nuitka具有更高的效率和安全性。不过，Nuitka的上手难度稍高。

数列极限

数列极限的定义

对于无穷实数数列\(\{a_{n}\}\)，当\(n\)无限增大时，\(a_{n}\)无限接近实数\(a\)，那么我们称数列\(\{a_{n}\}\)的极限（limit）是\(a\)，记作\(\lim\limits_{n \to \infty} a_{n} = a\)。
更加严格地说，对于任意的\(\varepsilon > 0\)，都存在正整数\(N\)，使得对于任意的\(n \ge N\)，都有\(|a_{n} - a| < \varepsilon\)，那么数列\(\{a_{n}\}\)的极限是\(a\)，\(\lim\limits_{n \to \infty} a_{n} = a\)。

数列

数列（sequence）是数字的序列。一般来说，数列是一个定义在正整数集的子集上的函数，记\(a_{n} = f(n)\)，则数列可以表示为\(\{a_{n}\}\)。数列中的每一个数称为数列的项（term），\(a_{1}\)称为数列的首项。定义在无限集合上的数列叫做无穷数列（infinite sequence）；否则叫做有穷数列（finite sequence），最后一项称为数列的末项。
有时候，我们也允许零甚至负数的下标，如\(a_{0}, a_{-1}\)等。我们通过额外的标注来表现这些，例如\(\{a_{n}\}_{0}^{\infty}\)表示一个从\(a_{0}\)开始的无穷数列。

坐标系

极坐标系

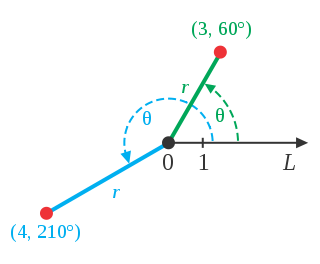
在平面内取一点\(O\)，称为极点（pole）；作一条以它为起点的射线\(x\)，称为极轴（polar axis）。这样就构成了极坐标系（polar coordinate system）。对极点外任意一点\(P\)，\(|OP|\)称为点\(P\)的极径（radial coordinate），一般用\(r\)表示；从极轴到射线\(OP\)的角，称为点\(P\)的极角（angular coordinate），一般用\(\theta\)表示。有序实数对\((r, \theta)\)就是点\(P\)的极坐标（polar coordinates）。

前言

日本古代史始于原始社会，终于1868年明治维新。其中，镰仓时代与室町时代又称日本中世史，安土桃山时代与江户时代又称日本近世史。

第一章“原始社会”介绍了旧石器时代（—前14000）、绳纹时代（前14000—前3世纪）与弥生时代（前3世纪—3世纪），第二章“奴隶社会”介绍了古坟时代（3世纪—592）；
第三章“大化改新与封建制的确立”介绍了飞鸟时代（592—710），第四章“奈良时代”介绍了奈良时代（710—794），第五章“平安时代”介绍了平安时代（794—1185）；
第六章“镰仓时代”介绍了镰仓时代（1185—1333），第七章“室町时代前期与南北朝时代”介绍了室町时代前期（1336—1467）与南北朝时代（1336—1392），第八章“室町时代后期与战国时代”介绍了室町时代后期（1467—1573）与战国时代（1467—1590）；
第九章“安土桃山时代”介绍了安土桃山时代（1573—1603），第十章“江户时代”介绍了黑船来航前的江户时代（1603—1853），第十一章“幕末的危机”介绍了江户时代末期（1853—1868）。