数列极限
数列极限的定义
对于无穷实数数列$\{a_{n}\}$,当$n$无限增大时,$a_{n}$无限接近实数$a$,那么我们称数列$\{a_{n}\}$的极限(limit)是$a$,记作$\lim\limits_{n \to \infty} a_{n} = a$。
更加严格地说,对于任意的$\varepsilon > 0$,都存在正整数$N$,使得对于任意的$n \ge N$,都有$|a_{n} - a| < \varepsilon$,那么数列$\{a_{n}\}$的极限是$a$,$\lim\limits_{n \to \infty} a_{n} = a$。
如果数列有极限,那么称数列收敛(convergent),于是$\{a_{n}\}$收敛于$a$。
如果数列没有极限,那么称数列发散(divergent)。发散数列可以左右摇摆,无法趋于某一个特定的值;发散数列也可以趋于无穷大。设数列$\{a_{n}\}$,如果对于任意的$M > 0$,都存在正整数$N$,使得对于任意的$n \ge N$,都有$|a_{n}| > M$,那么称数列$\{a_{n}\}$发散至无穷大,记作$\lim\limits_{n \to \infty} a_{n} = \infty$。更加准确地说,数列$\{a_{n}\}$发散至正无穷大或发散至负无穷大,分别记作$\lim\limits_{n \to \infty} a_{n} = +\infty$或$\lim\limits_{n \to \infty} a_{n} = -\infty$。
显而易见,$\lim\limits_{n \to \infty} a = a$;
$\lim\limits_{n \to \infty} \dfrac{1}{n} = 0$,进一步地,$\forall c > 0, \lim\limits_{n \to \infty} \dfrac{1}{n^{c}} = 0$;
设实数$q$满足$|q| < 1$,则$\lim\limits_{n \to \infty} q^{n} = 0$。
极限可以进行四则运算:
设$\lim\limits_{n \to \infty} a_{n} = a, \lim\limits_{n \to \infty} b_{n} = b$,
$\lim\limits_{n \to \infty} (a_{n} \pm b_{n}) = a \pm b$;
$\lim\limits_{n \to \infty} a_{n} b_{n} = ab$,特别地,$\lim\limits_{n \to \infty} ca_{n} = ca$,其中$c$为常数;
若$b \ne 0$,则$\lim\limits_{n \to \infty} \dfrac{a_{n}}{b_{n}} = \dfrac{a}{b}$。
有一些数列是求和的形式。如果$S_{n} = \sum\limits_{i=1}^{n} a_{i}$是收敛数列,极限是$S$,那么称级数(series)$\sum\limits_{n=1}^{\infty} a_{n}$收敛,记作$\sum\limits_{n=1}^{\infty} a_{n} = S$。$S$称为级数$\sum\limits_{n=1}^{\infty} a_{n}$的和(sum),$S_{n}$称为级数的部分和(partial sum)。
收敛数列的性质
收敛数列有三条基本性质。
唯一性:
收敛数列$\{a_{n}\}$的极限唯一。
证明:
设数列$\{a_{n}\}$有极限$a, b$,则对于任意的$\varepsilon > 0$,都存在正整数$N$,使得对于任意的$n \ge N$,都有$|a_{n} - a| < \dfrac{\varepsilon}{2}, |a_{n} - b| < \dfrac{\varepsilon}{2}$。那么$|a - b| = |(a_{n} - a) - (a_{n} - b)| \le |a_{n} - a| + |a_{n} - b| < \varepsilon$,于是$a = b$。$\Box$
如果改变数列中有限多项的值,不会改变数列的收敛性和极限。
有界性:
设数列$\{a_{n}\}$的极限是$a$,则数列$\{a_{n}\}$有界(bounded),即存在正数$M$,使得$\forall n \in \mathbb{N}^{\ast}, |a_{n}| \le M$。否则称数列$\{a_{n}\}$无界(unbounded)。
证明:
对于$\varepsilon = 1$,存在正整数$N$,使得$\forall n \ge N, |a_{n} - a| < 1$。那么$|a_{n}| \le |a_{n} - a| + |a| < |a| + 1$。令$M = \max(|a_{1}|, \cdots, |a_{N - 1}|, |a| + 1)$,则对于任意的$n$,如果$n \le N - 1$,那么$|a_{n}| \le \max(|a_{1}|, \cdots, |a_{N - 1}|) \le M$;如果$n \ge N$,那么$|a_{n}| < |a| + 1 \le M$。$\Box$
如果实数$l$满足$a > l$,那么存在正整数$N$,使得对于任意的$n \ge N$,都有$a_{n} > l$。$>$换成$<$同样成立。
如果实数$l$满足存在正整数$N$,使得对于任意的$n \ge N$,都有$a_{n} \ge l$,那么$a \ge l$。$\ge$换成$\le$同样成立。
保序性:
设数列$\{a_{n}\}, \{b_{n}\}$的极限分别是$a, b$,如果$a > b$,那么存在正整数$N$,使得对于任意的$n \ge N$,都有$a_{n} > b_{n}$;如果存在正整数$N$,使得对于任意的$n \ge N$,都有$a_{n} \ge b_{n}$,那么$a \ge b$。
计算极限时,把需要求的数列夹在两个极限相等的数列之间,就是非常实用的迫敛定理(squeeze theorem):
如果数列$\{b_{n}\}, \{c_{n}\}$的极限都是$a$,数列$\{a_{n}\}$满足存在正整数$N$,使得对于任意的$n \ge N$,都有$b_{n} \le a_{n} \le c_{n}$,那么数列$\{a_{n}\}$收敛于$a$。
证明:
对于任意的$\varepsilon > 0$,都存在正整数$N$,使得对于任意的$n \ge N$,都有$|b_{n} - a| < \varepsilon, |c_{n} - a| < \varepsilon$,那么$b_{n} > a - \varepsilon, c_{n} < a + \varepsilon$。$n \ge N$时,$b_{n} \le a_{n} \le c_{n}$,这样$a - \varepsilon < b_{n} \le a_{n} \le c_{n} < a + \varepsilon$,也就是$|a_{n} - a| < \varepsilon$,根据极限定义,$\{a_{n}\}$的极限是$a$。$\Box$
设$\{a_{n}\}$是数列,$n_{1} < n_{2} < \cdots < n_{k} < \cdots$是正整数数列,那么$a_{n_{1}}, a_{n_{2}}, \cdots, a_{n_{k}}, \cdots$组成一个数列,称为数列$\{a_{n}\}$的子列(subsequence),记作$\{a_{n_{k}}\}$。
设数列$\{a_{n}\}$收敛于$a$,那么对于任意的$\varepsilon > 0$,都存在正整数$N$,使得对于任意的$n \ge N$,都有$|a_{n} - a| < \varepsilon$。设$\{a_{n}\}$的子列是$\{a_{n_{k}}\}$。因为$\{n_{k}\}$是递增的无穷数列,所以发散至无穷大。因此存在正整数$K$,使得对于任意的$k \ge K$都有$n_{k} \ge N$,这样就有$|a_{n_{k}} - a| < \varepsilon$。所以$\{a_{n_{k}}\}$也收敛于$a$。
这样就得出:数列与其子列的收敛性和极限相同。
如果一个数列有不收敛的子列,或者某些不同子列收敛于不同的值,那么就可以说明数列发散。
实数的完备性
极限还有一些特殊性质,它们是实数集的本质特征。我们从完备性公理(completeness axiom)开始:
设$A, B$是$\mathbb{R}$的非空子集,如果$\forall a \in A, \forall b \in B, a \le b$,那么存在实数$c$,使得$\forall a \in A, \forall b \in B, a \le c \le b$。
完备性公理说明,实数是没有间隙的,任何两个不交叉的实数集合中间必然可以插入一个实数。
设$X$是$\mathbb{R}$的非空子集,如果实数$a$满足$\forall x \in X, x \le a$,那么称$a$是$X$的一个上界(upper bound);如果$\forall x \in X, x \ge a$,那么称$a$是$X$的一个下界(lower bound)。上界或下界可能不存在,也可能存在无穷多个。如果$X$既有上界又有下界,那么称集合$X$有界(bounded),否则称无界(unbounded)。
我们通常会寻找最小上界或者最大下界。一般地,设$a$是$X$的上界,如果对于任意的$b > a$,$b$也是$X$的上界,那么称$a$是$X$的上确界(supremum),记作$\sup X$;类似地有下确界(infimum),记作$\inf X$。
实际上,确界存在定理(least-upper-bound property)有:
任何有上界或下界的集合一定有上确界或下确界。
证明:
设$\mathbb{R}$的子集$X$有上界,$Y$是$X$的所有上界组成的集合,则$\forall x \in X, \forall y \in Y, x \le y$。根据完备性公理,存在实数$c$,使得$\forall x \in X, \forall y \in Y, x \le c \le y$。$x \le c$说明$c$是$X$的一个上界,而对任意的$z > c$,根据$c \le y$,$z$是上界。因此$c$是上确界。下确界同理。$\Box$
单调有界定理(monotone convergence theorem)说明了实数集和极限的关联:
单调有界数列收敛。
证明:
设递增数列$\{a_{n}\}$满足$\forall n \in \mathbb{N}^{\ast}, |a_{n}| \le M$,$X$是$\{a_{n}\}$的所有项组成的集合,则$M$是$X$的上界。根据确界存在定理,$X$有上确界,记为$a$。则对于任意的$\varepsilon > 0$,存在$a_{N} \in X$,使得$a_{N} > a - \varepsilon$。因为$\{a_{n}\}$递增,所以对于任意的$n \ge N$,都有$a_{n} \ge a_{N} > a - \varepsilon$,又$a_{n} \le a < a + \varepsilon$,所以$|a_{n} - a| < \varepsilon$,根据极限定义,数列$\{a_{n}\}$收敛于$a$。递减数列同理。$\Box$
我们可以借此定义常数$\mathrm{e}$。令$e_{n} = (1 + \dfrac{1}{n})^{n}$,根据单调有界定理,如果数列$\{e_{n}\}$单调有界,那么它就有极限。
由平均值不等式,$e_{n} = (1 + \dfrac{1}{n})^{n} \cdot 1 \le \left(\dfrac{n (1 + \dfrac{1}{n}) + 1}{n + 1} \right)^{n + 1} = (1 + \dfrac{1}{n + 1})^{n + 1} = e_{n + 1}$,所以$\{e_{n}\}$是递增数列。
因此$e_{n} \ge e_{1} = 2$,由二项式定理,
所以$2 \le e_{n} < 3$,$\{e_{n}\}$有界。
因此数列$\{e_{n}\}$有极限,记为$\mathrm{e}$,也就是$\mathrm{e} = \lim\limits_{n \to \infty} (1 + \dfrac{1}{n})^{n}$。
区间套定理(nested intervals theorem)进一步刻画了实数的完备性:
设一系列闭区间$I_{n} = [a_{n}, b_{n}]$满足$I_{1} \supseteq I_{2} \supseteq \cdots \supseteq I_{n} \supseteq \cdots$,且$\lim\limits_{n \to \infty} (b_{n} - a_{n}) = 0$,则存在唯一实数$\xi$属于所有的闭区间$I_{n}$,即$\bigcap\limits_{n = 1}^{\infty} I_{n} = \{\xi\}$。
证明:
由条件,数列$\{a_{n}\}$是递增数列,数列$\{b_{n}\}$是递减数列,且$a_{n}, b_{n} \in [a_{1}, b_{1}]$。根据单调有界定理,两个数列都有极限,分别记为$a, b$。那么$b - a = \lim\limits_{n \to \infty} b_{n} - \lim\limits_{n \to \infty} a_{n} = \lim\limits_{n \to \infty} (b_{n} - a_{n}) = 0$,即$a = b$。令$\xi = a = b$,则$\xi$就是所求的唯一实数。$\Box$
区间套定理可以形象地表述为:一系列逐渐缩小且环环相套的区间,区间长度缩小到$0$时,区间必缩成一个点。
从区间套定理出发,可以得到列紧性定理(sequential compactness theorem):
有界数列一定存在收敛子列。
证明:
设有界数列$\{a_{n}\}$满足$\forall n \in \mathbb{N}^{\ast}, a_{n} \in [c, d]$。把区间分为$[c, \dfrac{c + d}{2}], [\dfrac{c + d}{2}, d]$两半,则至少有一半含有数列$\{a_{n}\}$中的无限项,将这一半区间记为$I_{1} = [c_{1}, d_{1}]$;把$I_{1}$也这样分为两半,则至少有一半含有$\{a_{n}\}$中的无限项,将这一半区间记为$I_{2} = [c_{2}, d_{2}]$;依此类推,得到一系列区间$I_{n} = [c_{n}, d_{n}]$,且满足$I_{1} \supseteq I_{2} \supseteq \cdots \supseteq I_{n} \supseteq \cdots$,$\lim\limits_{n \to \infty} (d_{n} - c_{n}) = \lim\limits_{n \to \infty} \dfrac{1}{2^{n}} (d - c) = 0$。根据区间套定理,$\lim\limits_{n \to \infty} c_{n} = \lim\limits_{n \to \infty} d_{n} = a$。
在区间$I_{1}$中取一个项$a_{n_{1}}$;在区间$I_{2}$中取一个项$a_{n_{2}}$,且$n_{2} > n_{1}$;如此下去,得到子列$a_{n_{k}} \in I_{k}$,即$c_{k} \le a_{n_{k}} \le d_{k}$。根据迫敛定理,$\{a_{n_{k}}\}$收敛于$a$。$\Box$
设$\{a_{n}\}$是数列,如果对于任意的$\varepsilon > 0$,都存在正整数$N$,使得对于任意的$m, n \ge N$,都有$|a_{m} - a_{n}| < \varepsilon$,那么称$\{a_{n}\}$为柯西列(Cauchy sequence)。
柯西收敛准则(Cauchy completeness)有:
数列$\{a_{n}\}$收敛的充要条件是$\{a_{n}\}$是柯西列。
证明:
必要性:设$\{a_{n}\}$收敛于$a$,则对于任意的$\varepsilon > 0$,都存在正整数$N$,使得对于任意的$n \ge N$,都有$|a_{n} - a| < \dfrac{\varepsilon}{2}$。这样,对于任意的$m, n \ge N$,就有$|a_{m} - a_{n}| = |(a_{m} - a) - (a_{n} - a)| \le |a_{m} - a| + |a_{n} - a| < \varepsilon$。
充分性:如果$\{a_{n}\}$是柯西列,那么对于$\varepsilon = 1$,存在正整数$N$,使得对于任意的$m, n \ge N$,都有$|a_{m} - a_{n}| < 1$。这样$|a_{n} - a_{N}| < 1$,得到$|a_{n}| \le |a_{N}| + 1$。令$M = \max(|a_{1}|, \cdots, |a_{N - 1}|, |a_{N}| + 1)$,则$\forall n \in \mathbb{N}^{\ast}, |a_{n}| \le M$,所以$\{a_{n}\}$有界。根据列紧性定理,$\{a_{n}\}$存在收敛子列$\{a_{n_{k}}\}$,设$\{a_{n_{k}}\}$收敛于$a$。对于任意的$\varepsilon > 0$,都存在正整数$K$,使得对于任意的$k \ge K$,都有$|a_{n_{k}} - a| < \dfrac{\varepsilon}{2}$。根据柯西列的定义,对于任意的$m, n \ge N$,都有$|a_{m} - a_{n}| < \dfrac{\varepsilon}{2}$。取$k \ge K$使得$n_{k} \ge N$,则对于任意的$n \ge N$,$|a_{n} - a| \le |a_{n} - a_{n_{k}}| + |a_{n_{k}} - a| < \varepsilon$,所以$\{a_{n}\}$收敛于$a$。$\Box$
函数极限
初等函数
我们研究过常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数,它们经过有限次加、减、乘、除、乘方、开方和复合运算,得到的函数称为初等函数(elementary function)。初等函数是数学中最基本的一类函数,具有相当重要的性质。
例如,正整数次幂函数和常数函数之间可以运算得到形如$f(x) = \sum\limits_{k=0}^{n} a_{k} x^{k}$的函数,称为多项式函数(polynomial function);两个多项式函数相除,得到形如$f(x) = \sum\limits_{k=0}^{n} \dfrac{a_{k} x^{k}}{b_{k} x^{k}}$的函数,称为有理函数(rational function)。
双曲函数(hyperbolic function)也是一种初等函数,常见的有:
- 双曲正弦:$\sinh x = \dfrac{\mathrm{e}^{x} - \mathrm{e}^{-x}}{2}$
- 双曲余弦:$\cosh x = \dfrac{\mathrm{e}^{x} + \mathrm{e}^{-x}}{2}$
- 双曲正切:$\tanh x = \dfrac{\sinh x}{\cosh x} = \dfrac{\mathrm{e}^{x} - \mathrm{e}^{-x}}{\mathrm{e}^{x} + \mathrm{e}^{-x}}$
双曲函数有类似三角函数的性质,例如$\sinh(x + y) = \sinh x \cosh y + \cosh x \sinh y$。
函数极限的定义
与数列极限类似,我们考虑自变量趋于无穷大时函数值的趋势。如果实数$l$满足,对于任意的$\varepsilon > 0$,存在$\delta > 0$,使得对于任意的$|x| > \delta$,都有$|f(x) - l| < \varepsilon$,那么$x$趋于无穷大时,$f(x)$的极限(limit)是$l$,记作$\lim\limits_{x \to \infty} f(x) = l$。
从图像来看,$\lim\limits_{x \to \infty} f(x) = l$意味着当$|x|$足够大时,函数图像将会落在由直线$y = l + \varepsilon, y = l - \varepsilon$所围成的一个足够狭长的区域内。
把条件$|x| > \delta$改为$x > \delta$或$x < -\delta$,就是$x \to \pm \infty$时函数极限的定义,分别记作$\lim\limits_{x \to +\infty} f(x) = l$和$\lim\limits_{x \to -\infty} f(x) = l$。
类似地,还有$x \to \infty$时,$f(x)$发散至无穷大:$\lim\limits_{x \to \infty} f(x) = \infty$。更加准确地说,可以写成$\lim\limits_{x \to +\infty} f(x) = +\infty, \lim\limits_{x \to -\infty} f(x) = +\infty, \lim\limits_{x \to +\infty} f(x) = -\infty, \lim\limits_{x \to -\infty} f(x) = -\infty$。
与数列极限不同的是,我们还要考虑自变量趋于某个有限值时函数值的趋势。设函数$f$在$(x_{0} - \delta_{0}, x_{0}) \cup (x_{0}, x_{0} + \delta_{0})$有定义,如果实数$l$满足,对于任意的$\varepsilon > 0$,存在$\delta > 0$满足$\delta < \delta_{0}$,使得只要$0 < |x - x_{0}| < \delta$,就有$|f(x) - l| < \varepsilon$,那么$x$趋于$x_{0}$时,$f(x)$的极限是$l$,记作$\lim\limits_{x \to x_{0}} f(x) = l$。
$(x_{0} - \delta_{0}, x_{0}) \cup (x_{0}, x_{0} + \delta_{0})$称为$x_{0}$的一个去心邻域(deleted neighbourhood),$(x_{0} - \delta_{0}, x_{0} + \delta_{0})$则称为$x_{0}$的一个邻域(neighbourhood)。如果把$x$限制在足够小的去心邻域内,对应的$f(x)$也就会被限制在足够小的邻域内。之所以是去心邻域而非邻域,是因为函数在某一点没有定义时,也存在这一点的极限。
类似地,$x \to x_{0}$时,也可以趋于无穷大:$\lim\limits_{x \to x_{0}} f(x) = \infty$,进一步可以写成$\lim\limits_{x \to x_{0}} f(x) = +\infty, \lim\limits_{x \to x_{0}} f(x) = -\infty$。
有时,函数只在$x_{0}$的一侧有定义,或者函数在$x_{0}$的两侧定义方式不同。这时,设函数$f$在$x_{0}$的一个左邻域$(x_{0} - \delta_{0}, x_{0})$有定义,如果实数$l$满足,对于任意的$\varepsilon > 0$,存在$\delta > 0$满足$\delta < \delta_{0}$,使得只要$-\delta < x - x_{0} < 0$,就有$|f(x) - l| < \varepsilon$,那么我们定义$f(x)$在$x_{0}$的左极限(left limit)是$l$,记作$\lim\limits_{x \to x_{0}^{-}} f(x) = l$。
设函数$f$在$x_{0}$的一个右邻域$(x_{0}, x_{0} + \delta_{0})$有定义,如果实数$l$满足,对于任意的$\varepsilon > 0$,存在$\delta > 0$满足$\delta < \delta_{0}$,使得只要$0 < x - x_{0} < \delta$,就有$|f(x) - l| < \varepsilon$,那么定义$f(x)$在$x_{0}$的右极限(right limit)是$l$,记作$\lim\limits_{x \to x_{0}^{+}} f(x) = l$。
显然,函数在$x_{0}$存在极限的充要条件是:它在$x_{0}$的左极限和右极限存在且相等。
函数极限的性质与运算
函数极限的性质和数列极限类似,证明过程也可以参照数列极限。
唯一性:
若函数$f(x)$在$x_{0}$有极限,则极限唯一。
有界性:
设函数$f(x)$在$x_{0}$有极限$l$,则$f(x)$在$x_{0}$附近有界,即存在正数$M$和$\delta$,使得只要$0 < |x - x_{0}| < \delta$,就有$|f(x)| \le M$。
若$a < l < b$,则在$x_{0}$附近有$a < f(x) < b$。
保序性:
设$\lim\limits_{x \to x_{0}} f(x) = l_{1}, \lim\limits_{x \to x_{0}} g(x) = l_{2}$,若在$x_{0}$附近有$f(x) \ge g(x)$,则$l_{1} \ge l_{2}$;若$l_{1} > l_{2}$,则在$x_{0}$附近有$f(x) > g(x)$。
四则运算:
设$\lim\limits_{x \to x_{0}} f(x) = l_{1}, \lim\limits_{x \to x_{0}} g(x) = l_{2}$,
$\lim\limits_{x \to x_{0}} (f(x) \pm g(x)) = l_{1} \pm l_{2}$;
$\lim\limits_{x \to x_{0}} f(x) g(x) = l_{1} l_{2}$,特别地,$\lim\limits_{x \to x_{0}} cf(x) = cl_{1}$,其中$c$为常数;
若$l_{2} \ne 0$,则$\lim\limits_{x \to x_{0}} \dfrac{f(x)}{g(x)} = \dfrac{l_{1}}{l_{2}}$。
迫敛定理:
设在$x_{0}$附近有$g(x) \le f(x) \le h(x)$,且$\lim\limits_{x \to x_{0}} g(x) = \lim\limits_{x \to x_{0}} h(x) = l$,则$\lim\limits_{x \to x_{0}} = l$。
函数与数列的不同点在于可以复合。设函数$f, g$分别在$x_{0}, t_{0}$附近有定义,且在$t_{0}$附近$t \ne t_{0}$时$g(t) \ne x_{0}$,如果$\lim\limits_{x \to x_{0}} f(x) = l, \lim\limits_{t \to t_{0}} g(t) = x_{0}$,那么$\lim\limits_{t \to t_{0}} f(g(t)) = l$。
这样,求一些函数极限的问题就可以通过换元转化成两个较简单的极限问题。
海涅定理(Heine theorem)沟通了函数极限与数列极限:
设函数$f$在$x_{0}$附近有定义,则$\lim\limits_{x \to x_{0}} f(x) = l$的充要条件是:对于任何收敛于$x_{0}$的数列$\{a_{n}\} (a_{n} \ne x_{0})$,都有$\lim\limits_{n \to \infty} f(a_{n}) = l$。
证明:
必要性:如果$\lim\limits_{x \to x_{0}} f(x) = l$,那么对于任意的$\varepsilon > 0$,存在$\delta > 0$,使得只要$0 < |x - x_{0}| < \delta$,就有$|f(x) - l| < \varepsilon$。设$\{a_{n}\} (a_{n} \ne x_{0})$收敛于$x_{0}$,则存在正整数$N$,使得对于任意的$n \ge N$,都有$|a_{n} - x_{0}| < \delta$。因为$a_{n} \ne x_{0}$,所以$0 < |x - x_{0}| < \delta$,这样$\forall n \ge N, |f(a_{n}) - l| < \varepsilon$,也就是$\lim\limits_{n \to \infty} f(a_{n}) = l$。
充分性:对于任何收敛于$x_{0}$的数列$\{a_{n}\} (a_{n} \ne x_{0})$,都有$\lim\limits_{n \to \infty} f(a_{n}) = l$。用反证法,假设$\lim\limits_{x \to x_{0}} f(x) = l$不成立,则存在$\varepsilon > 0$,使得对于任意的$\delta > 0$,都存在$x_{\delta}$,使得即使$0 < |x_{\delta} - x_{0}| < \delta$,仍有$|f(x_{\delta}) - l| \ge \varepsilon$。令$\delta_{n} = \dfrac{1}{n}, a_{n} = x_{\delta_{n}}$,则$0 < |a_{n} - x_{0}| < \dfrac{1}{n}, |f(a_{n}) - l| \ge \varepsilon$。由前者可得$\lim\limits_{n \to \infty} a_{n} = x_{0}$,由后者可得$\{f(a_{n})\}$不收敛于$l$,矛盾。$\Box$
海涅定理可以用于检验极限是否存在。如果存在收敛于$x_{0}$的两个数列$\{a_{n}\}, \{b_{n}\}$,使得$\{f(a_{n})\}, \{f(b_{n})\}$趋于不同的值或者发散,则函数$f(x)$在$x_{0}$不存在极限。
重要极限与兰道记号
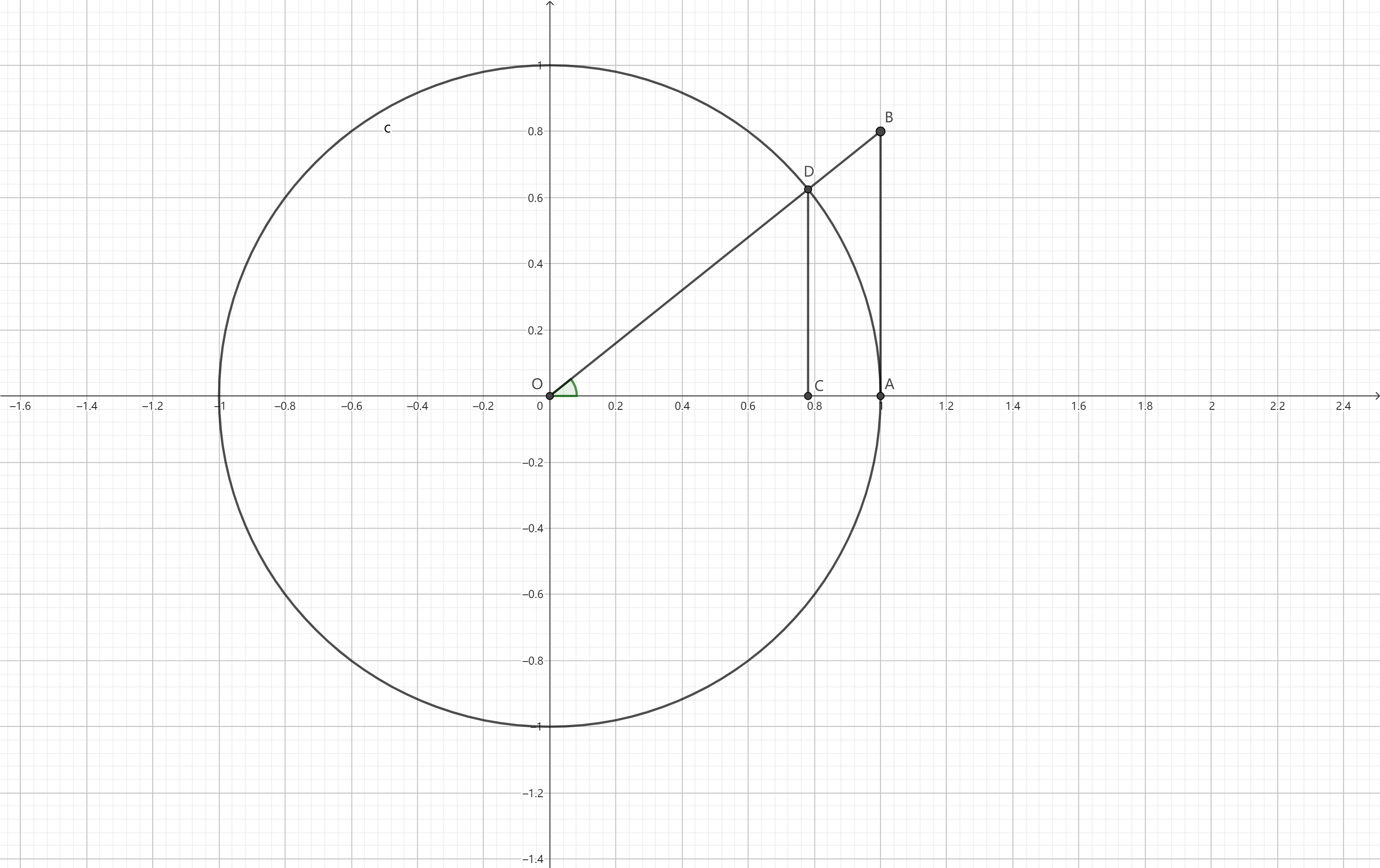
设$x \in (0, \dfrac{\pi}{2})$。如图,单位圆中$\angle AOD = x$,$CD \perp OA$交$OA$于点$C$,$AB \perp OA$交$OD$于点$B$。显然,$|CD| = \sin x, |AB| = \tan x$。因为三角形$AOD$的面积小于扇形$AOD$的面积又小于三角形$AOB$的面积,所以$\dfrac{1}{2} \sin x < \dfrac{1}{2} x < \dfrac{1}{2} \tan x$。
因此$x \in (0, \dfrac{\pi}{2})$时,有$\sin x < x < \tan x$。
这样在$x \in \mathbb{R}$时,就有$|\sin x| \le |x|$,等号成立当且仅当$x = 0$。
从而可以得出一个重要极限:
证明:
设$x \in (0, \dfrac{\pi}{2})$,则由上面的不等式,$1 < \dfrac{x}{\sin x} < \dfrac{1}{\cos x}$,即$\cos x < \dfrac{\sin x}{x} < 1$。再由上面的不等式,$\cos x = 1 - 2\sin^{2} \dfrac{x}{2} > 1 - 2 (\dfrac{x}{2})^{2} = 1 - \dfrac{x^{2}}{2}$,所以$1 - \dfrac{x^{2}}{2} < \dfrac{\sin x}{x} < 1$。因为$\lim\limits_{x \to 0^{+}} (1 - \dfrac{x^{2}}{2}) = 1$,根据迫敛定理,$\lim\limits_{x \to 0^{+}} \dfrac{\sin x}{x} = 1$。而令$y = -x$,有$\lim\limits_{x \to 0^{-}} \dfrac{\sin x}{x} = \lim\limits_{y \to 0^{+}} \dfrac{\sin(-y)}{-y} = \lim\limits_{y \to 0^{+}} \dfrac{\sin y}{y} = 1$,所以$\lim\limits_{x \to 0} \dfrac{\sin x}{x} = 1$。$\Box$
这个极限在物理学和天文学中很重要。如果$\theta$是一个很小的正角,那么可以认为$\sin \theta \approx \tan \theta \approx \theta$。
我们知道$\mathrm{e} = \lim\limits_{n \to \infty} (1 + \dfrac{1}{n})^{n}$,而对于函数$(1 + \dfrac{1}{x})^{x}$,结果也是一样的。这就是另一个重要极限:
证明:
我们可以把一般情况化为整数的情况。因为$[x] \le x < [x] + 1$,根据指数函数和幂函数的单调性,有$(1 + \dfrac{1}{[x] + 1})^{[x]} < (1 + \dfrac{1}{x})^{x} < (1 + \dfrac{1}{[x]})^{[x] + 1}$。因为$\lim\limits_{x \to +\infty} [x] = +\infty$,所以$\lim\limits_{x \to +\infty} (1 + \dfrac{1}{[x] + 1})^{[x]} = \lim\limits_{x \to +\infty} (1 + \dfrac{1}{[x] + 1})^{[x] + 1} (1 + \dfrac{1}{[x] + 1})^{-1} = \mathrm{e}$以及$\lim\limits_{x \to +\infty} (1 + \dfrac{1}{[x]})^{[x] + 1} = \lim\limits_{x \to +\infty} (1 + \dfrac{1}{[x]})^{[x]} (1 + \dfrac{1}{[x]}) = \mathrm{e}$。根据迫敛定理,$\lim\limits_{x \to +\infty} (1 + \dfrac{1}{x})^{x} = \mathrm{e}$。而令$y = -x$,有$\lim\limits_{x \to -\infty} (1 + \dfrac{1}{x})^{x} = \lim\limits_{y \to +\infty} (1 - \dfrac{1}{y})^{-y} = \lim\limits_{y \to +\infty} (1 + \dfrac{1}{y - 1})^{y} = \lim\limits_{y \to +\infty} (1 + \dfrac{1}{y - 1})^{y - 1} (1 + \dfrac{1}{y - 1}) = \mathrm{e}$,所以$\lim\limits_{x \to \infty} (1 + \dfrac{1}{x})^{x} = \mathrm{e}$。$\Box$
对这个极限进行倒数代换,就得到类似的$\lim\limits_{x \to 0} (1 + x)^{\frac{1}{x}} = \mathrm{e}$。
如果函数$f, g$在$x_{0}$附近有定义,满足$\lim\limits_{x \to x_{0}} \dfrac{f(x)}{g(x)} = 1$,则称$x \to x_{0}$时$f, g$等价,记作$f(x) \sim g(x) (x \to x_{0})$。例如,由第一个重要极限可得$\sin x \sim x (x \to 0)$。等价的函数在乘除因式里可以相互替换。
如果$\lim\limits_{x \to x_{0}} \dfrac{f(x)}{g(x)} = 0$,则称$x \to x_{0}$时$f$比$g$低阶,$g$比$f$高阶,记作$f(x) = o(g(x)) (x \to x_{0})$。“低阶”指的就是增长较慢,例如$x^2 = o(x) (x \to 0)$。
如果$\left|\dfrac{f(x)}{g(x)} \right|$在$x_{0}$附近有界,即存在$M > 0$使得$\left|\dfrac{f(x)}{g(x)} \right| \le M$,则称$x \to x_{0}$时$f$的阶不超过$g$,记作$f(x) = O(g(x)) (x \to x_{0})$。例如,$\sinh x = O(\mathrm{e}^{x})$。特别地,$f(x) = O(1) (x \to x_{0})$表示$f$在$x_{0}$附近有界。
等价符号$\sim$、小$o$符号和大$O$符号由德国数学家爱德蒙·兰道(Edmund Landau,1877—1938)推广,统称为兰道记号(Landau notation),在渐进分析中相当常用。兰道记号有一些性质:
- $o(f(x)) + o(f(x)) = o(f(x))$
- $o(f(x)) \cdot o(g(x)) = o(f(x) g(x))$
- $o(f(x)) = O(f(x))$
注意兰道记号中的等号不同于一般的等号,它仅仅表示等号左边满足等号右边的性质。最后一条不能反过来,$O(f(x)) = o(f(x))$不一定成立。
函数的连续性
连续性的定义
我们曾用$\varepsilon - \delta$语言定义过连续性:设函数$f$在$x_{0}$附近有定义,如果对于任意的$\varepsilon > 0$,都存在$\delta > 0$,使得只要$|x - x_{0}| < \delta$,就有$|f(x) - f(x_{0})| < \varepsilon$,那么称$f$在点$x_{0}$连续。
现在可以用极限写出更加简洁的定义:设函数$f$在$x_{0}$附近有定义,如果$\lim\limits_{x \to x_{0}} f(x) = f(x_{0})$,那么称$f$在点$x_{0}$连续。
从这一定义看,连续性就是某一点处的极限等于函数值。当自变量从$x_{0}$变为$x$时,就产生了一个增量$\Delta x = x - x_{0}$,函数值也对应产生一个增量$\Delta y = f(x) - f(x_{0}) = f(x_{0} + \Delta x) - f(x_{0})$,连续性实际上也就是说$\lim\limits_{\Delta x \to 0} \Delta y = 0$。
如果函数在某一点不连续,那么称它在这一点间断。如果函数$f$在开区间$I$的每一点都连续,那么称函数$f$是开区间$I$上的连续函数(continuous function)。
函数$f$在点$x_{0}$连续当且仅当$\lim\limits_{x \to x_{0}^{-}} f(x) = \lim\limits_{x \to x_{0}^{+}} f(x) = f(x_{0})$。我们可以同样定义与左右极限对应的左右连续的概念:如果$\lim\limits_{x \to x_{0}^{-}} f(x) = f(x_{0})$,那么称$f$在$x_{0}$左连续;如果$\lim\limits_{x \to x_{0}^{+}} f(x) = f(x_{0})$,那么称$f$在$x_{0}$右连续。
对于闭区间$I$上的函数$f$,如果$f$在区间内每一点都连续,且在左端点左连续,右端点右连续,那么称函数$f$是闭区间$I$上的连续函数。
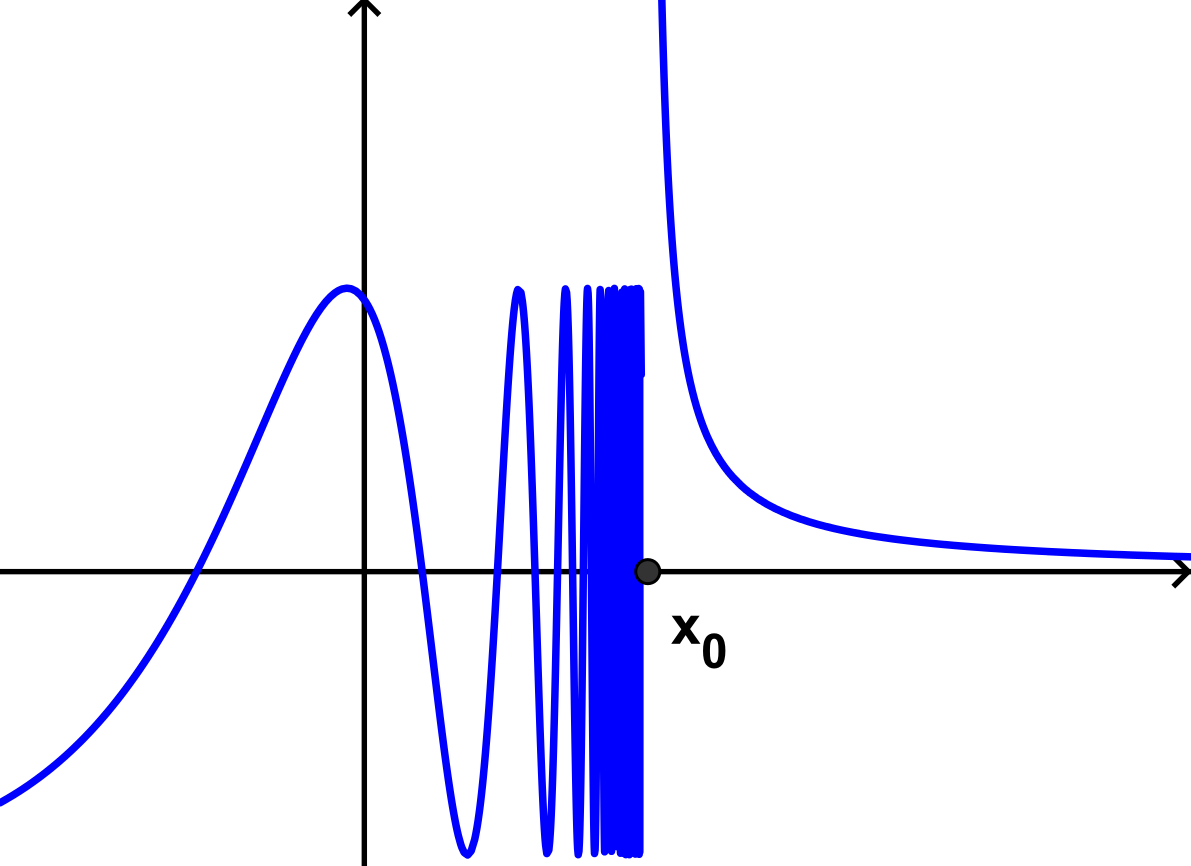
我们再来考虑间断点(discontinuity)。间断点有三种情况:
- 函数在某一点存在极限,即左右极限相等,但与函数值不相等,或者函数在这一点没有定义,即$\lim\limits_{x \to x_{0}^{-}} f(x) = \lim\limits_{x \to x_{0}^{+}} f(x) \ne f(x_{0})$。这类间断点称为可去间断点(removable discontinuity)。因为只要修改这一点,就能变为连续函数,例如$g(x) = \begin{cases} f(x), & x \ne x_{0} \\ \lim\limits_{x \to x_{0}^{-}} f(x), & x = x_{0} \end{cases}$。
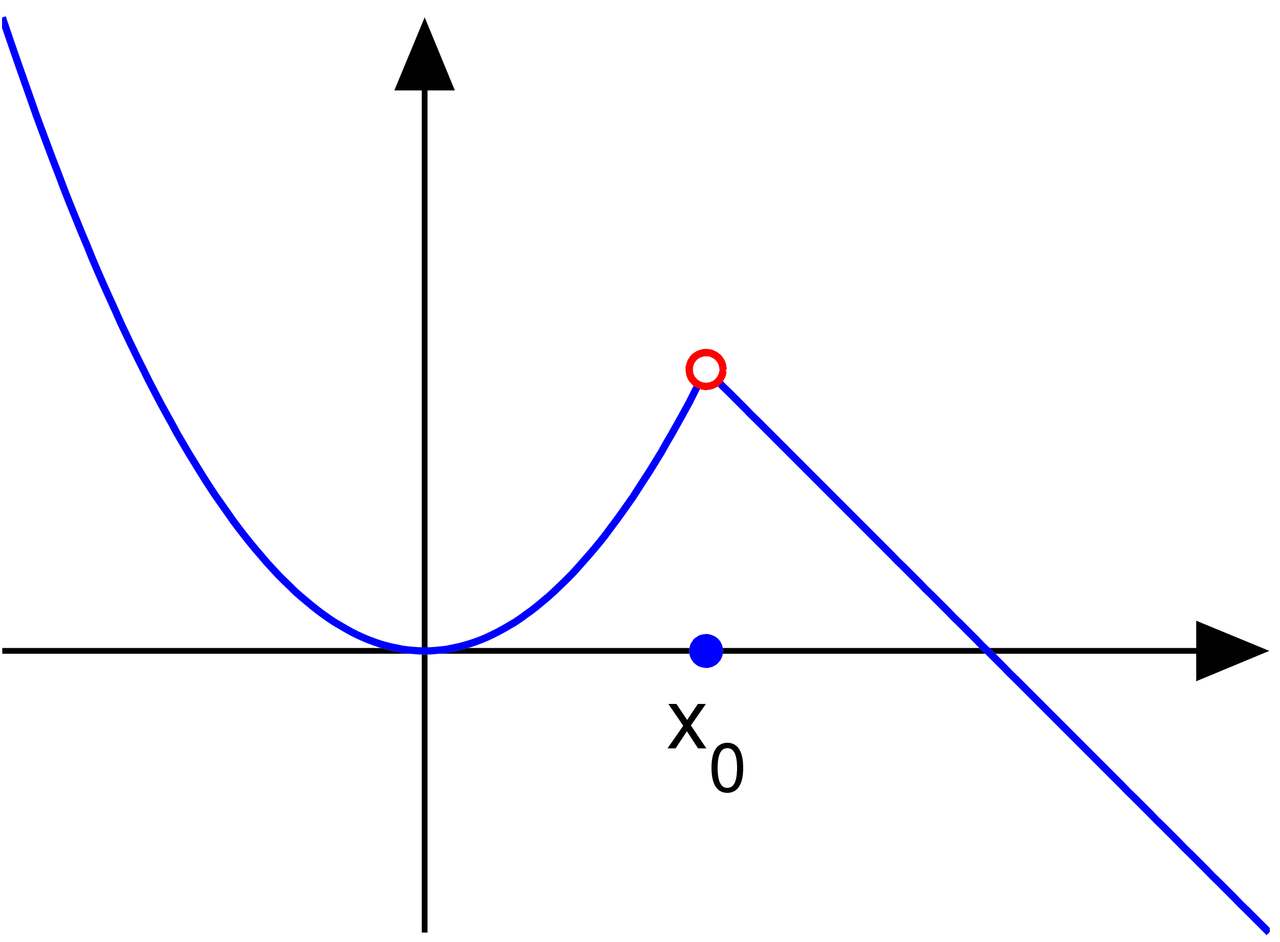
- 函数在某一点的左右极限存在但不相等,即$\lim\limits_{x \to x_{0}^{-}} f(x) \ne \lim\limits_{x \to x_{0}^{+}} f(x)$。这类间断点称为跳跃间断点(jump discontinuity)。因为函数在$x_{0}$处发生了$|\lim\limits_{x \to x_{0}^{+}} f(x) - \lim\limits_{x \to x_{0}^{-}} f(x)|$的跳跃。
可去间断点和跳跃间断点统称为第一类间断点。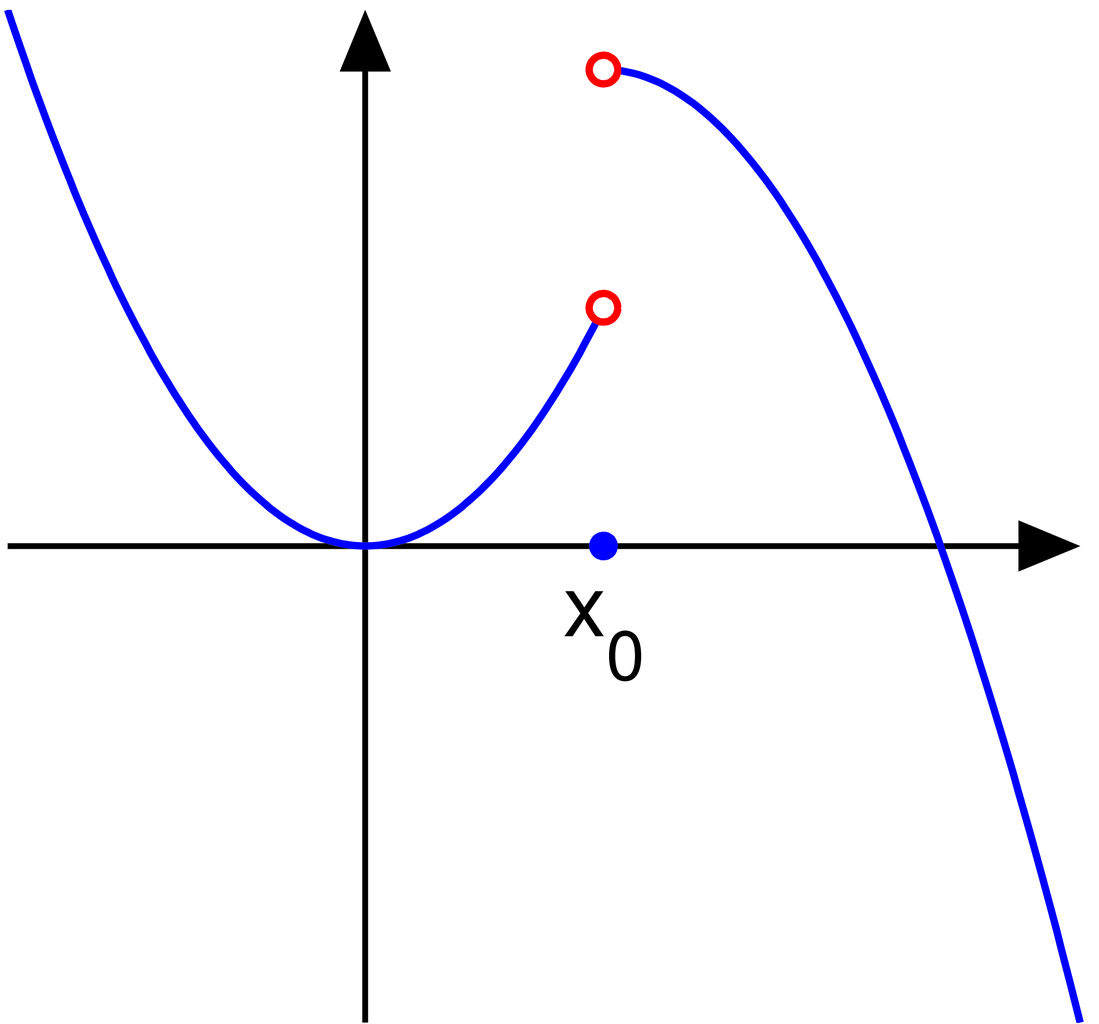
- 函数在某一点的左右极限至少有一个不存在。这类间断点称为第二类间断点(essential discontinuity)。例如,对于狄利克雷函数(Dirichlet function)$D(x) = \begin{cases} 1, & x \in \mathbb{Q} \\ 0, & x \in \mathbb{R} - \mathbb{Q} \end{cases}$,任意的$x_{0} \in \mathbb{R}$都是其第二类间断点。
连续函数的四则运算和复合同样具有连续性。
设函数$f(x), g(x)$在$x_{0}$连续,则$f(x) \pm g(x), f(x) g(x), \dfrac{f(x)}{g(x)} (g(x_{0}) \ne 0)$也在$x_{0}$连续。
设函数$u = g(x)$在区间$I$有定义,$y = f(u)$在区间$J$有定义,且$g(I) \subseteq J$。若$g$在$x_{0} \in I$处连续,$f$在$u_{0} = g(x_{0})$处连续,则复合函数$f \circ g$在$x_{0}$处连续。即$\lim\limits_{x \to x_{0}} f(g(x)) = f(\lim\limits_{x \to x_{0}} g(x)) = f(g(x_{0}))$,连续函数复合的极限运算可以层层向内进行。
此外,连续函数的反函数同样是连续函数。
连续函数还具有局部保号性:
设函数$f$在$x_{0}$处连续,且$f(x_{0}) \ne 0$,则存在$\delta > 0$,使得只要$0 < |x - x_{0}| < \delta$,就有$f(x) f(x_{0}) > 0$。
初等函数的连续性
因为$\lim\limits_{x \to x_{0}} x = x_{0}$,乘法得到$\lim\limits_{x \to x_{0}} x^{k} = x_{0}^{k}$,再加法得到$\lim\limits_{x \to x_{0}} \sum\limits_{k=0}^{n} a_{k} x^{k} = \sum\limits_{k=0}^{n} a_{k} x_{0}^{k}$。
所以多项式函数是连续函数。
根据和差化积公式,$|\sin x - \sin x_{0}| = 2 |\sin \dfrac{x - x_{0}}{2} \cos \dfrac{x + x_{0}}{2}| \le 2 |\sin \dfrac{x - x_{0}}{2}| \le |x - x_{0}|$。对于任意的$\varepsilon > 0$,令$\delta = \varepsilon$,则$0 < |x - x_{0}| < \delta$时,$|\sin x - \sin x_{0}| \le |x - x_{0}| < \varepsilon$,所以$\lim\limits_{x \to x_{0}} \sin x = \sin x_{0}$,$\sin x$是连续函数。
其它三角函数均可由$\sin x$导出,所以三角函数是连续函数。
反三角函数是三角函数的反函数,所以反三角函数也是连续函数。
设$a > 0$。令$y = x - x_{0}$,则$\lim\limits_{x \to x_{0}} y = 0$。所以$\lim\limits_{x \to x_{0}} (a^{x} - a^{x_{0}}) = a^{x_{0}} \lim\limits_{x \to x_{0}} (a^{x - x_{0}} - 1) = a^{x_{0}} \lim\limits_{y \to 0} (a^{y} - 1) = 0$,即$\lim\limits_{x \to x_{0}} a^{x} = a^{x_{0}}$。
所以指数函数是连续函数。
对数函数是指数函数的反函数,所以对数函数也是连续函数。
设$f(x) = x^{\alpha}, x \in (0, +\infty) (\alpha \ne 0)$,则$f(x) = x^{\alpha} = \mathrm{e}^{\alpha \ln x}$,是连续函数的复合。
所以幂函数是连续函数。
所有初等函数都可以由以上函数运算得到。所以,初等函数具有连续性。初等函数在其定义域内是连续函数。若初等函数$f$在$x_{0}$附近有定义,则$\lim\limits_{x \to x_{0}} f(x) = f(x_{0})$。
闭区间上连续函数的性质
如果函数在一个闭区间上连续,那么有零点定理:
设函数$f$在$[a, b]$上连续,且$f(a) f(b) < 0$,则存在$\xi \in (a, b)$使得$f(\xi) = 0$。
证明:
不妨设$f(a) < 0 < f(b)$。把区间$[a, b]$分为$[a, \dfrac{a + b}{2}], [\dfrac{a + b}{2}, b]$两半,如果$f(\dfrac{a + b}{2}) = 0$,定理得证,否则$f(\dfrac{a + b}{2})$必与$f(a), f(b)$之一异号。将异号的这一半区间记为$I_{1} = [a_{1}, b_{1}]$,则$f(a_{1}) < 0 < f(b_{1})$;把$I_{1}$也这样分为两半,如此下去,得到一系列区间$I_{n} = [a_{n}, b_{n}]$,且满足$I_{1} \supseteq I_{2} \supseteq \cdots \supseteq I_{n} \supseteq \cdots$,$\lim\limits_{n \to \infty} (b_{n} - a_{n}) = \lim\limits_{n \to \infty} \dfrac{1}{2^{n}} (b - a) = 0$,$f(a_{n}) < 0 < f(b_{n})$。根据区间套定理,有$\xi = \lim\limits_{n \to \infty} a_{n} = \lim\limits_{n \to \infty} b_{n}$。由海涅定理,$f(\xi) = \lim\limits_{n \to \infty} f(a_{n}) \le 0 \le \lim\limits_{n \to \infty} f(b_{n}) = f(\xi)$,即$f(\xi) = 0$。$\Box$
上述证明过程体现了二分法(bisection method)的算法思想。二分法可以用于计算函数零点,通过不断把零点所在区间对半分来逼近零点,步骤如下:
- 指定误差值$\varepsilon$。
- 找出一个区间$[a, b]$使得$f(a) f(b) < 0$。
- 令$x = \dfrac{a + b}{2}$。若$f(a) f(x) < 0$,则取$[a, x]$为新的区间;若$f(b) f(x) < 0$,则取$[x, b]$为新的区间。
- 重复第3步,直到$|f(x)| < \varepsilon$,此时取$x$作为零点。
零点定理推广可得介值定理(intermediate value theorem):
设函数$f$在$[a, b]$上连续,若对于任意实数$u$有$f(a) < u < f(b)$,则存在$\xi \in (a, b)$使得$f(\xi) = u$。
根据连续性的定义,如果函数$f$在点$x_{0}$连续,那么对于$\varepsilon = 1$,存在$\delta > 0$,使得只要$|x - x_{0}| < \delta$,就有$|f(x) - f(x_{0})| < 1$。这样,$|f(x)| < 1 + |f(x_{0})|$,函数$f$在区间$(x_{0} - \delta, x_{0} + \delta)$有界。
进一步推广,如果函数$f$在$[a, b]$上连续,则$f$在$[a, b]$上有界,即存在正数$M$,使得$\forall x \in [a, b], |f(x)| \le M$。
更进一步有最值定理(extreme value theorem):
设函数$f$在$[a, b]$上连续,则$f$在$[a, b]$上存在最大值和最小值,即存在$x_{1}, x_{2} \in [a, b]$,使得$\forall x \in [a, b], f(x_{1}) \le f(x) \le f(x_{2})$。
介值定理和最值定理说明,连续函数将闭区间映射为闭区间。正是如此,求出闭区间上连续函数的最大值和最小值,才确定了函数的值域。

