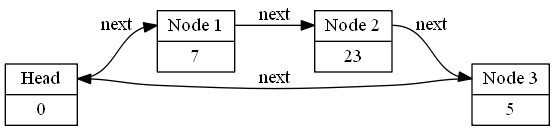
ST表
简介
区间最值查询(range minimum/maximum query,
RMQ)问题主要有两种解决方法:ST表(sparse
table)和线段树(segment
tree),本文主要讲ST表。
ST表适合解决静态RMQ问题,即:
给定\(n\)个数,进行\(m\)次询问。对于每次询问,都需要回答区间\([l, r]\)中的最小值或最大值。
如果用暴力做法,每次都对区间\([x, y]\)扫描一遍,肯定是过不了的,所以我们需要引入ST表。ST表可以实现\(O(n \log n)\)的预处理和\(O(1)\)的查询。
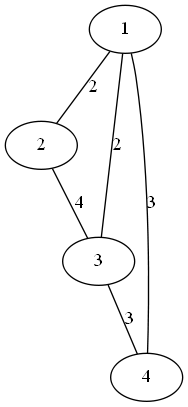 下图就是它的最小生成树,边权和为
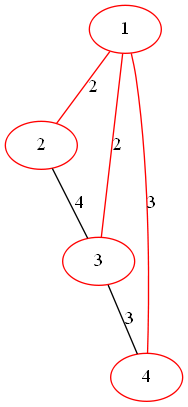
下图就是它的最小生成树,边权和为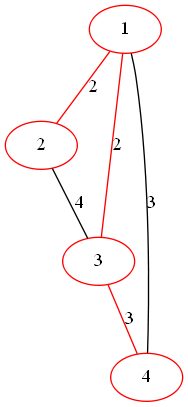 不过对于一部分图,比如上面炒的栗子,最小生成树有多种解,但是边权和是不变的:
不过对于一部分图,比如上面炒的栗子,最小生成树有多种解,但是边权和是不变的:
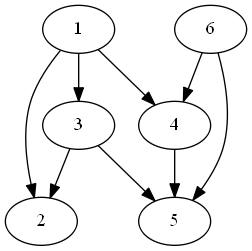 当然,拓扑排序的结果肯定是不唯一的,比如图片中
当然,拓扑排序的结果肯定是不唯一的,比如图片中