学习笔记·古典立体几何

立体几何基本公理

平面几何研究的对象是点（point）与直线（line），而在立体几何中，平面（plane）也成为了研究对象。
尽管平面是无限延伸的，但在画图时我们用一个平行四边形来表示平面。平面可以用一个希腊字母表示，例如$\alpha, \beta$；也可以用平面内的点表示，例如平面$ABCD$。

平面几何是在欧几里得（Euclid，约前325—约前270）的五条公理上建立起来的，这些公理在立体几何中仍然成立，并与下面的三条立体几何基本公理共同构成了立体几何。

公理1：过不在同一直线上的三点有且只有一个平面。
这条公理也可以表述为“不共线的三点唯一确定一个平面”。
如果一个点$A$在平面$\alpha$内，那么记为$A \in \alpha$，否则记为$A \notin \alpha$。

公理2：若一条直线上的两个点都在平面内，则直线上的所有点都在该平面内。
如果一个点$A$在直线$l$上，那么记为$A \in l$，否则记为$A \notin l$。如果直线$l$上的所有点都在平面$\alpha$内，即直线$l$在平面$\alpha$内，那么记为$l \subset \alpha$，否则记为$l \not\subset \alpha$。这样的记号实际上是把直线和平面看作点的集合。
公理2就能用形式化的语言表示为：

$$A \in l, B \in l, A \in \alpha, B \in \alpha \Rightarrow l \subset \alpha$$

通过这两条公理，可以得到推论：

1. 经过一条直线和直线外一点有且只有一个平面；
2. 经过两条相交直线有且只有一个平面；
3. 经过两条平行直线有且只有一个平面。

证明：

1. 设直线$l$和点$A$。在直线$l$上取两点$B, C$，根据公理1，$A, B, C$三点确定唯一平面$\alpha$。因为$B, C \in l$，所以根据公理2，$l \subset \alpha$。$\Box$
2. 设直线$m, n$相交于点$A$。在直线$m$上取点$B$，且$A, B$不重合；在直线$n$上取点$C$，且$A, C$不重合。根据公理1，$A, B, C$三点确定唯一平面$\alpha$。因为$A, B \in m$，所以根据公理2，$m \subset \alpha$，同理$n \subset \alpha$。$\Box$
3. 设直线$m \parallel n$。在直线$m$上取两点$A, B$，在直线$n$上取点$C$。根据公理1，$A, B, C$三点确定唯一平面$\alpha$。因为$A, B \in m$，所以根据公理2，$m \subset \alpha$。在直线$n$上取除$C$外任意一点$D$，$A, B, D$三点确定平面$\beta$。因为$C \in \alpha, m \parallel n$，所以根据公理4，$n \subset \alpha$，所以$D \in \alpha$。因为$A, B, D$三点确定平面$\beta$，所以$\alpha, \beta$重合。$\Box$

两条直线不在同一平面内称为异面（skewness），异面直线没有公共点。两条直线有公共点称为相交（intersection），根据推论2，两条相交直线必然共面。无公共点且在同一平面内称为平行（parallelism）。

公理3：若两个不重合的平面有一个公共点，则它们有且只有一条过该点的公共直线，称为两个平面的交线（intersection line）。
如图，平面$\alpha, \beta$的交线是直线$l$，记为$\alpha \cap \beta = l$。
公理3用形式化的语言可以表示为：

$$P \in \alpha, P \in \beta \Rightarrow \alpha \cap \beta = l, P \in l$$

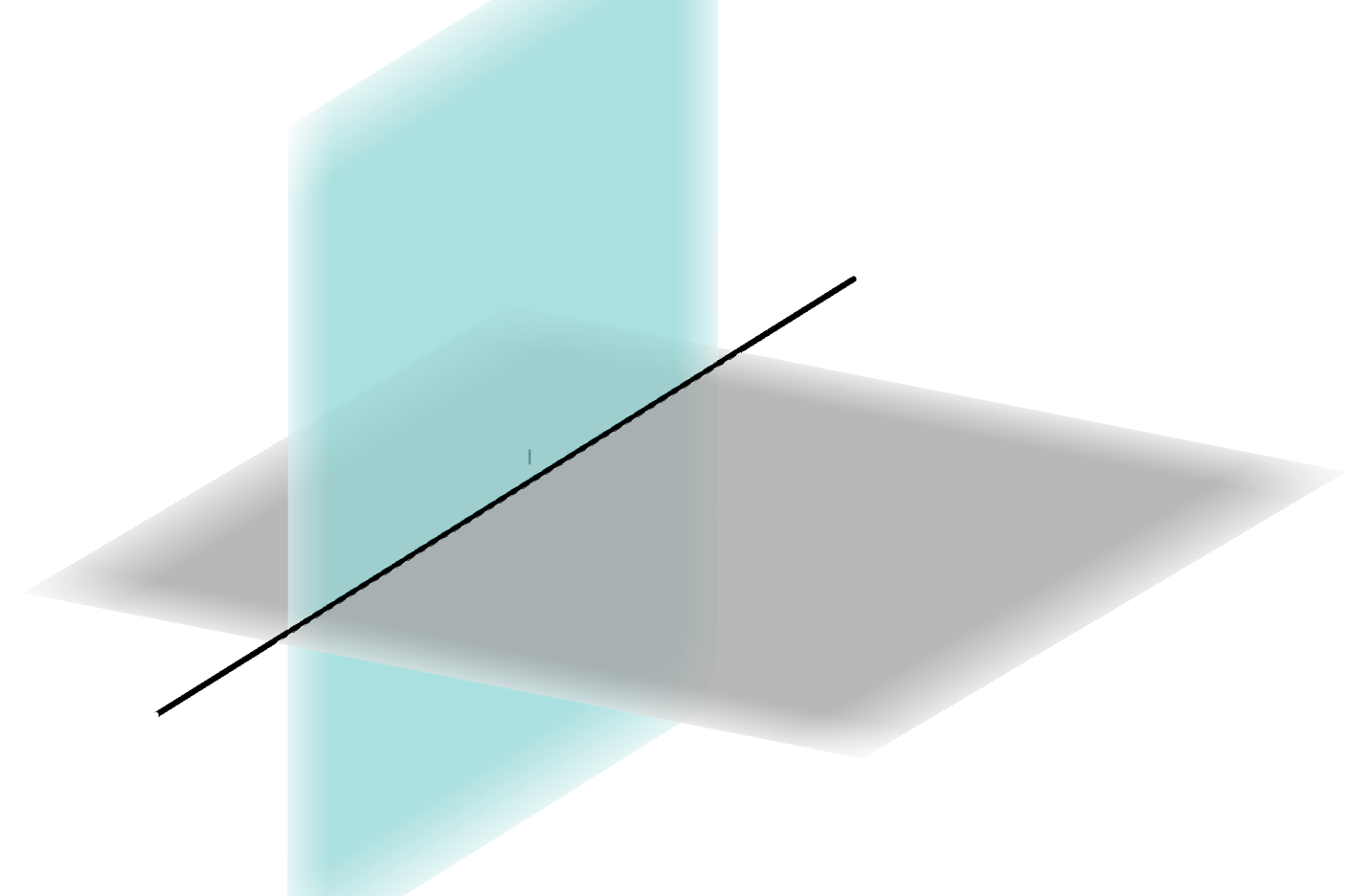
两个平面有交线称为相交（intersection），没有公共点称为平行（parallelism）。

对于直线和平面的位置关系：直线在平面内时，与平面有无数个公共点；直线与平面没有公共点称为平行（parallelism），既不在平面内又不与平面平行称为相交（intersection），这两者统称为在平面外。
相交的直线与平面有唯一的交点。
证明：
设直线$l$与平面$\alpha$相交。假设有两交点$P, Q$。$P, Q \in \alpha, P, Q \in l$，由公理2，$l \subset \alpha$，与相交的定义矛盾，故交点唯一。$\Box$。

此外，平面几何中的平行公理在立体几何中依然适用，这里一并列出。
公理4：过直线外一点，有且只有一条直线与该直线平行。

平行的判定与性质定理

直线与直线平行

由公理4，可以得到一个推论：
平行于同一直线的两条直线平行。
用形式化的语言表示就是：

$$l \parallel m, l \parallel n \Rightarrow m \parallel n$$

这条定理可以用于立体几何中直线与直线平行的判定。
证明这条定理需要用到后面的线面平行性质定理：
设$l, m$确定平面$\alpha$，$l, n$确定平面$\beta$。不妨设$\alpha, \beta$不是同一个平面，则$m \not\subset \beta$。用反证法，假设$m \nparallel n$。
若$m, n$共面，则一定相交，设交点为$P$。因为$\alpha \cap \beta = l, P \in m \subset \alpha, P \in n \subset \beta$，所以$P \in \alpha \cap \beta = l$，$l, m, n$三线共点，矛盾。
若$m, n$异面，因为$m \parallel l, l \subset \beta, m \not\subset \beta$，所以$\beta \parallel \beta$。任取点$Q \in n$，$m, Q$确定一个平面$\gamma$。设$\beta \cap \gamma = k$，则$Q \in k$，且$m \parallel k$。此时$m \parallel l$，若$l, k$相交，则情况同上，矛盾，因此$l \parallel k$。由于$m, n$异面，$n, k$必不是同一条直线，则过一点$Q$可以作$l$的两条平行线$n, k$，与公理4矛盾。$\Box$

与此相关还有一个性质定理：
若两个角的边分别对应平行，则这两个角相等或互补。

证明：
如图，$\angle ABC, \angle DEF$的两边对应平行，即$AB \parallel DE, BC \parallel EF$。不妨设$|AB| = |DE|, |BC| = |EF|$，$AB, DE$方向相同。
首先证明$EF, BC$方向相同时的情况。因为$AB \stackrel{\parallel}{=} DE$，所以$ABED$是平行四边形，可得$AD \stackrel{\parallel}{=} BE$。同理，$CF \stackrel{\parallel}{=} BE$，所以$AB \stackrel{\parallel}{=} CF$。因此，$ACFD$是平行四边形，$|AC| = |DF|$，故$\triangle ABC \cong \triangle DEF$，从而$\angle ABC = \angle DEF$。
对于$EF, BC$方向相反时的情况，可以反向延长其中一条线，然后得到类似的结论。$\Box$

直线与平面平行

对于直线与平面的平行关系，有判定定理：
若平面外一条直线与平面内的一条直线平行，则该直线与此平面平行。
用形式化的语言表示就是：

$$l \not\subset \alpha, m \subset \alpha, l \parallel m \Rightarrow l \parallel \alpha$$

用反证法可以证明：
假设$l \cap \alpha = P$。直线$l, m$确定一个平面$\beta$，那么$m = \alpha \cap \beta$。因为$l \subset \beta, m \subset \alpha$，所以$P \in \alpha \cap \beta = m$，得到$l \cap m = P$，与平行矛盾。$\Box$

对于直线与平面的平行关系，有性质定理：
若一条直线与一个平面平行，且过该直线的平面与此平面相交，则该直线与交线平行。
用形式化的语言表示就是：

$$l \parallel \alpha, l \subset \beta, \alpha \cap \beta = m \Rightarrow l \parallel m$$

证明：
因为$l \parallel \alpha$，所以$l \cap \alpha = \varnothing$，又$m \subset \alpha$，故$l \cap m = \varnothing$。$l, m \subset \beta$，由平行定义得到$l \parallel m$。

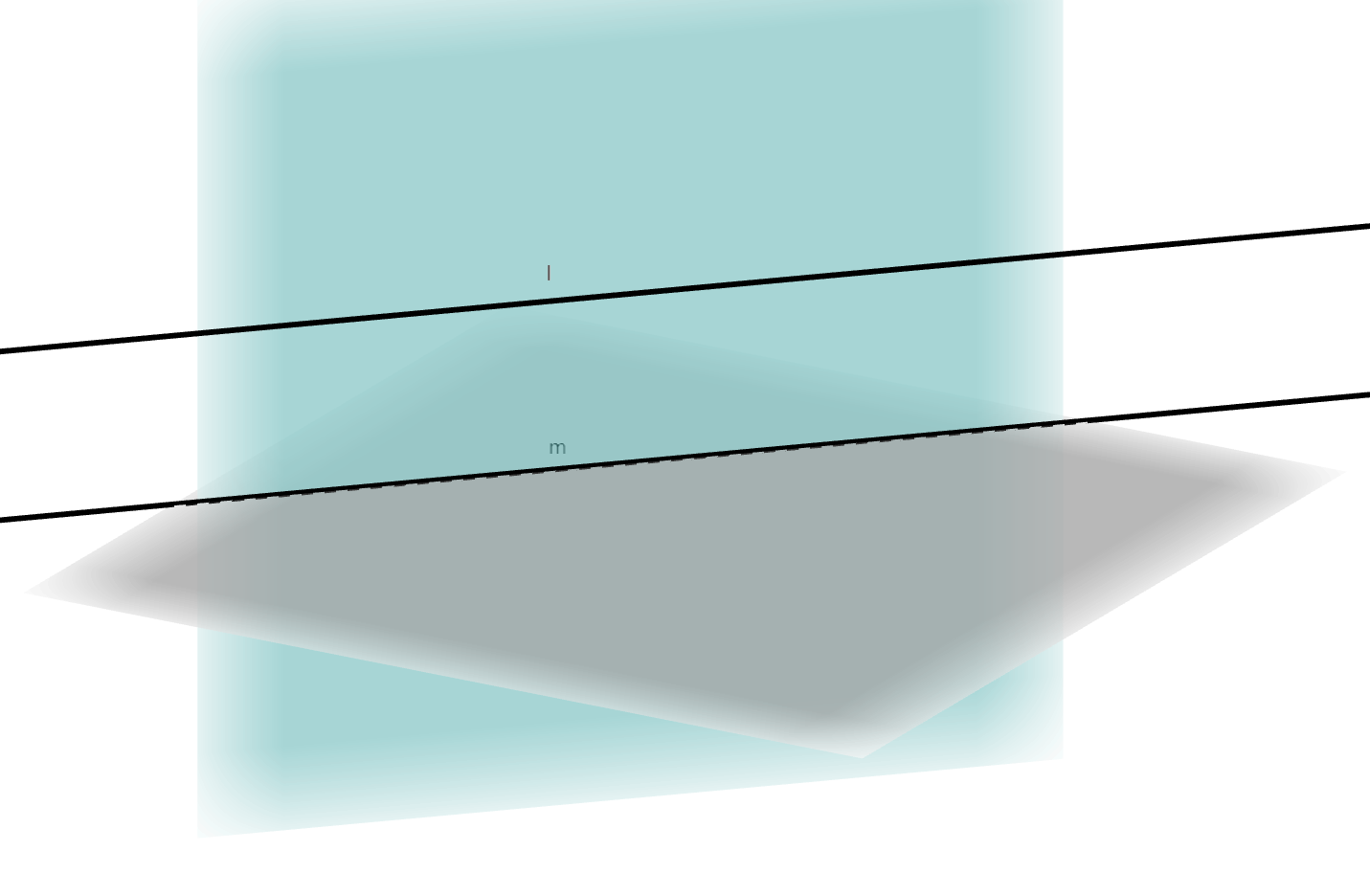
平面与平面平行

对于平面与平面的平行关系，有判定定理：
若一个平面内的两条相交直线都与另一个平面平行，则这两个平面平行。
用形式化的语言表示就是：

$$a \subset \beta, b \subset \beta, a \cap b = P, a \parallel \alpha, b \parallel \alpha \Rightarrow \alpha \parallel \beta$$

用反证法可以证明：
假设$\alpha \cap \beta = l$。不妨设$a \cap l = Q$，则$Q \in l = \alpha \cap \beta$，所以$a \cap \alpha = Q$，与$a \parallel \alpha$矛盾。若$a \parallel l, b \parallel l$，则过一点$P$可以作$l$的两条平行线$a, b$，矛盾。$\Box$

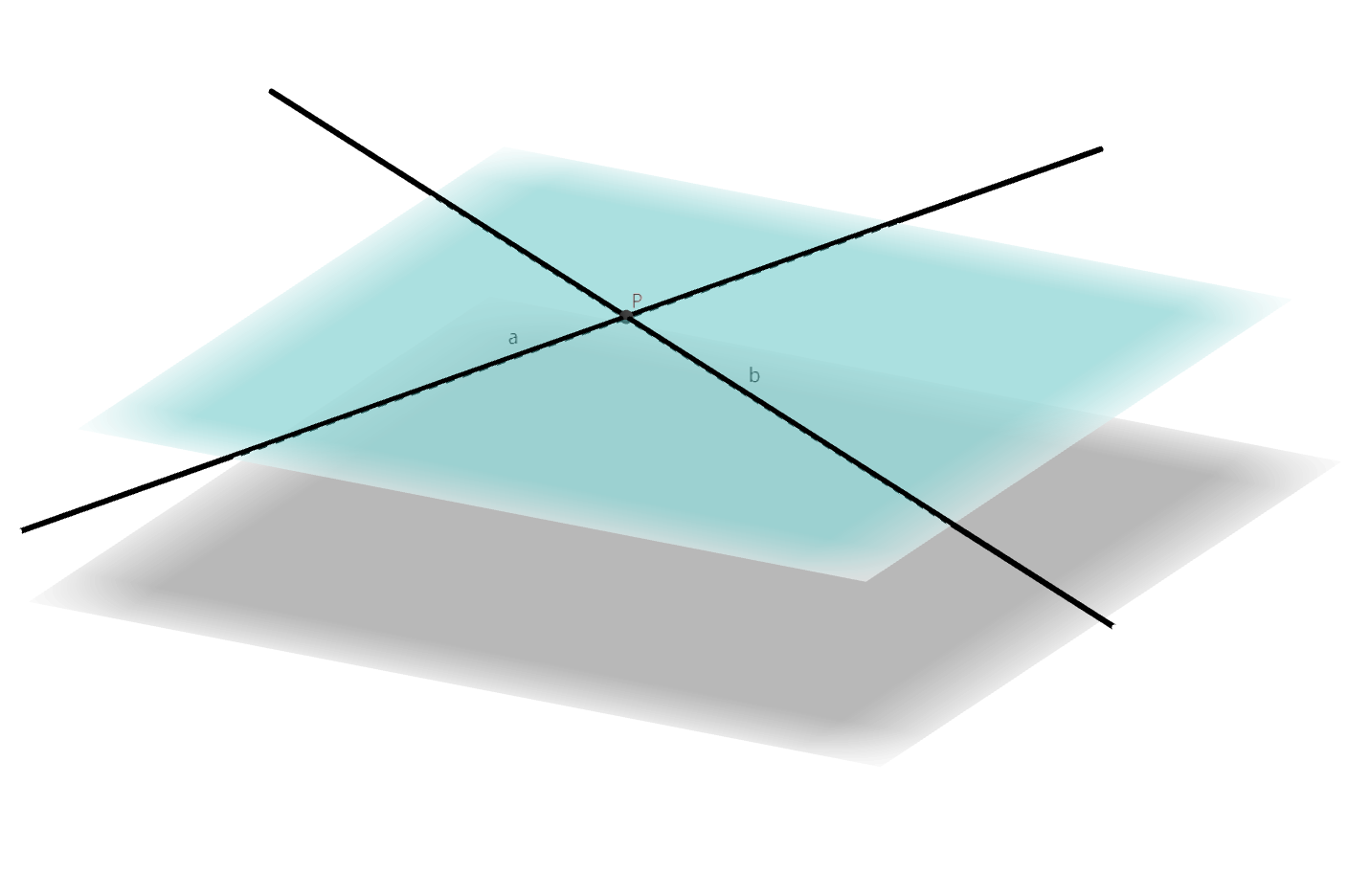
由这个判定定理可以得到推论：
若两个平面内各有一组相交直线对应平行，则这两个平面平行。

对于平面与平面的平行关系，有两条性质定理：

两个平面平行，则其中一个平面上任意一条直线与另一个平面平行。
用形式化的语言表示就是：

$$\alpha \parallel \beta, l \subset \alpha \Rightarrow l \parallel \beta$$

两个平面平行，若另一个平面与这两个平面相交，则两条交线平行。
用形式化的语言表示就是：

$$\alpha \parallel \beta, \gamma \cap \alpha = a, \gamma \cap \beta = b \Rightarrow a \parallel b$$

证明：
因为$\alpha \parallel \beta$，所以$\alpha \cap \beta = \varnothing$，又$a \subset \alpha, b \subset \beta$，故$a \cap b = \varnothing$。$a, b \subset \gamma$，由平行定义得到$a \parallel b$。$\Box$

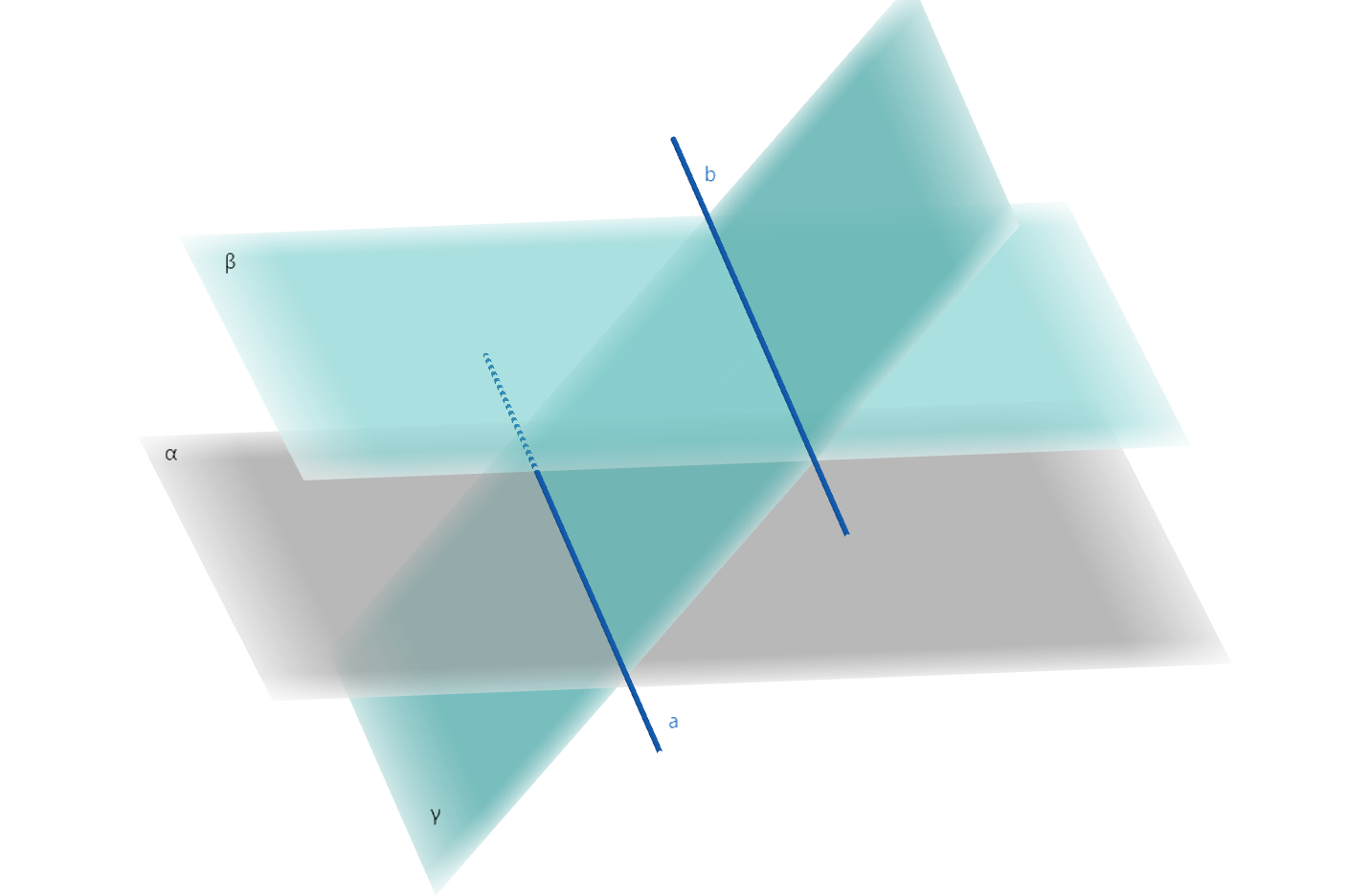
垂直的判定与性质定理

直线与直线垂直

在平面几何中，两条直线相交形成4个角，其中不大于$\dfrac{\pi}{2}$的称为两条直线的夹角。但在立体几何中，由于异面直线的存在，我们需要根据公理4，通过直线的平移来定义夹角。
设$a, b$是异面直线。在直线$a$上任取一点$A$，根据公理4，存在唯一的直线$b’$过点$A$且有$b’ \parallel b$。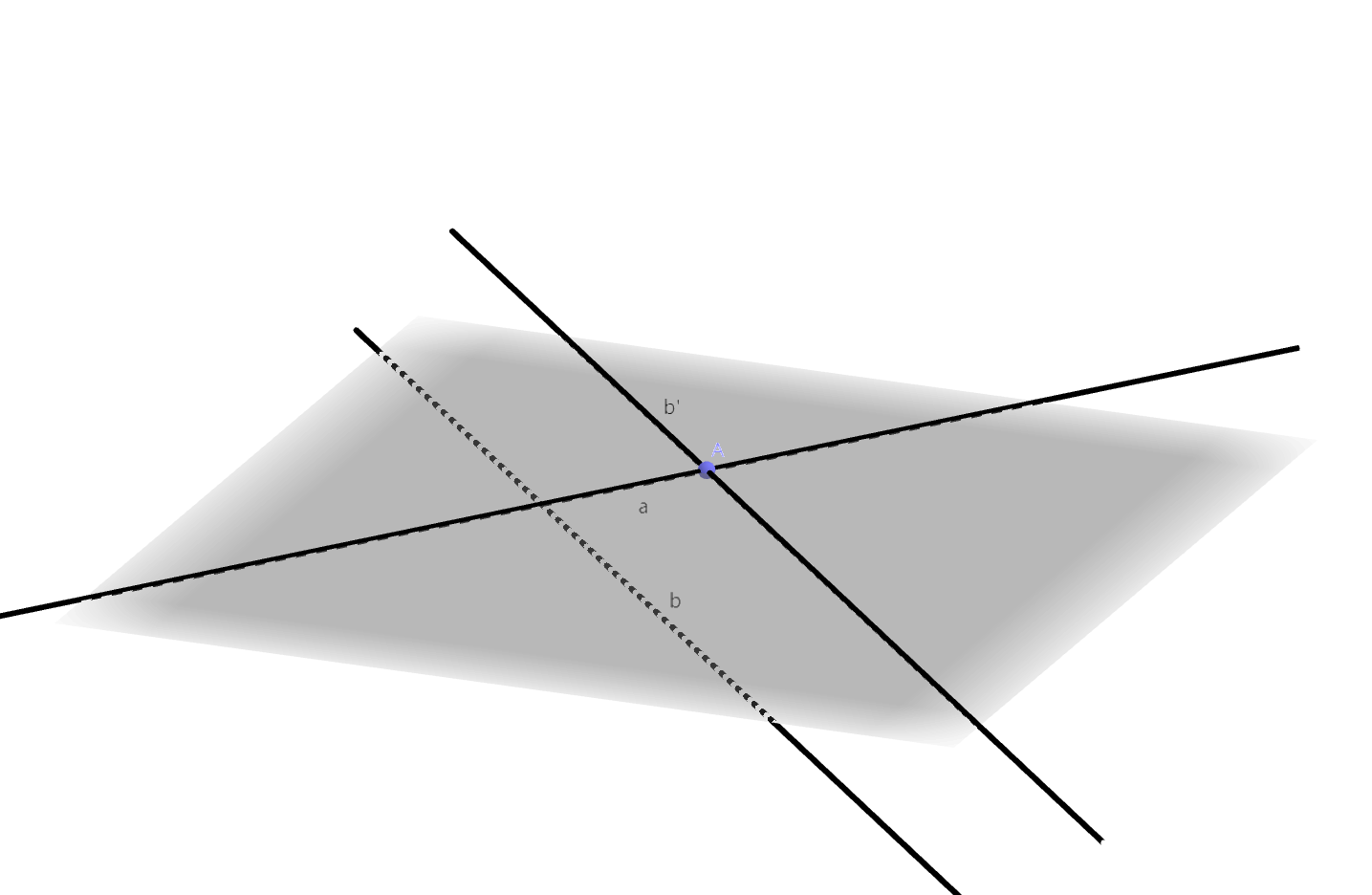

异面直线$a, b$的夹角（included angle）就是相交直线$a, b’$的夹角。夹角的范围是$[0, \dfrac{\pi}{2}]$。

规定平行直线的夹角是$0$。
如果两条直线$a, b$的夹角是$\dfrac{\pi}{2}$，那么称两条直线垂直（perpendicularity），记作$a \perp b$。

直线与平面垂直

如果直线与平面内任意一条直线都垂直，那么称该直线与此平面垂直。直线$l$与平面$\alpha$垂直记作$l \perp \alpha$，若$l \cap \alpha = P$，则称$P$为垂足（foot）。

直线与平面垂直的判定同样只需要两条相交直线：
若一条直线与平面内的两条相交直线都垂直，则该直线与平面垂直。
用形式化的语言表示就是：

$$l \perp a, l \perp b, a \subset \alpha, b \subset \alpha, a \cap b = P \Rightarrow l \perp \alpha$$

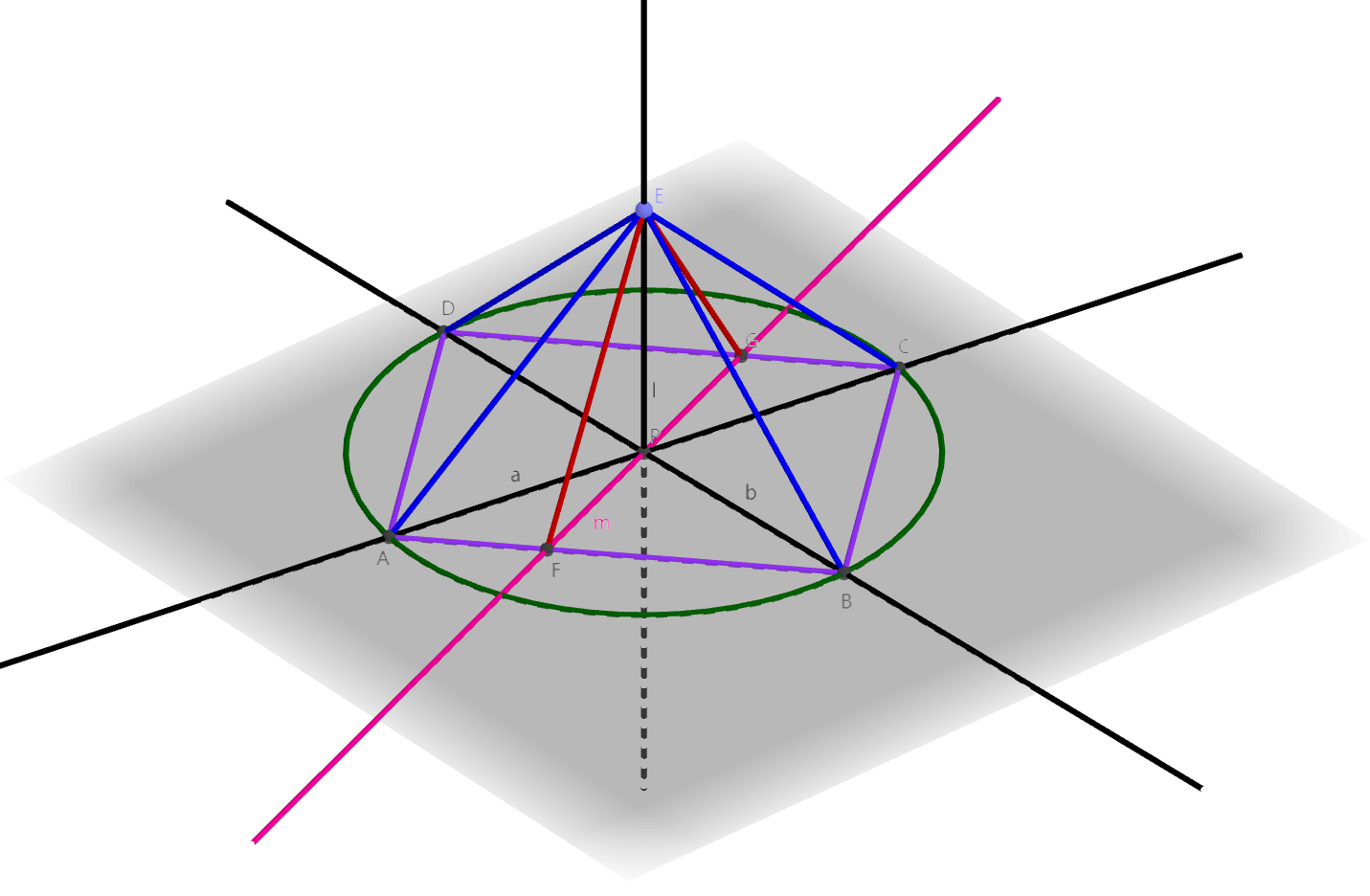
可以把所有直线都平移到一起来证明：
如图，设$l$过点$P$，以$P$为圆心，任意长度为半径作一个圆，交$a$于点$A, C$，交$b$于点$B, D$，任取$E \in l$。此时$|PA| = |PB| = |PC| = |PD|$，同时条件有$\angle EPA = \angle EPB = \angle EPV = \angle EPD = \dfrac{\pi}{2}$，得到$\triangle EPA \cong \triangle EPB \cong \triangle EPC \cong \triangle EPD$。这样有$|EA| = |EB| = |EC| = |ED|$，并由圆的性质有$|AB| = |CD|, |AD| = |BC|$。
任取直线$m \subset \alpha, P \in m$，$m$分别交$AB, CD$于点$F, G$。$ABCD$是矩形，因此有$AB \parallel CD$，得到比例关系$\dfrac{|AF|}{|GC|} = \dfrac{|FP|}{|PG|} = \dfrac{|AP|}{|PC|} = 1$，所以$|AF| = |CG|, |PF| = |PG|$。容易得到，$\triangle EAF \cong \triangle ECG$，从而$|EF| = |EG|$。而$|PF| = |PG|$，故$\triangle EPF \cong \triangle EPG$，$\angle EPF = \angle EPG = \dfrac{\pi}{2}$，因此$l \perp m$。
由$m$的任意性，得$l \perp \alpha$。$\Box$

过平面外一点，有且只有一条直线与该平面垂直。
证明：
存在性：设$O$为平面$\alpha$外一点。任取$m \subset \alpha$，过点$O$作$m$的垂线，垂足为$Q$；过点$Q$在平面$\alpha$内作$m$的垂线$n$；过点$O$作$n$的垂线，垂足为$P$。因为$OQ \perp m, PQ \perp m$，所以$m \perp $平面$OPQ$，得到$m \perp OP$。而$OP \perp n$，且$m \subset \alpha, n \subset \alpha, m \cap n = Q$，所以$OP \perp \alpha$。
唯一性：假设$OA, OB \perp \alpha$，则$OA, OB$相交于一点$O$。根据后面的线面垂直性质定理，$OA \parallel OB$，矛盾。$\Box$

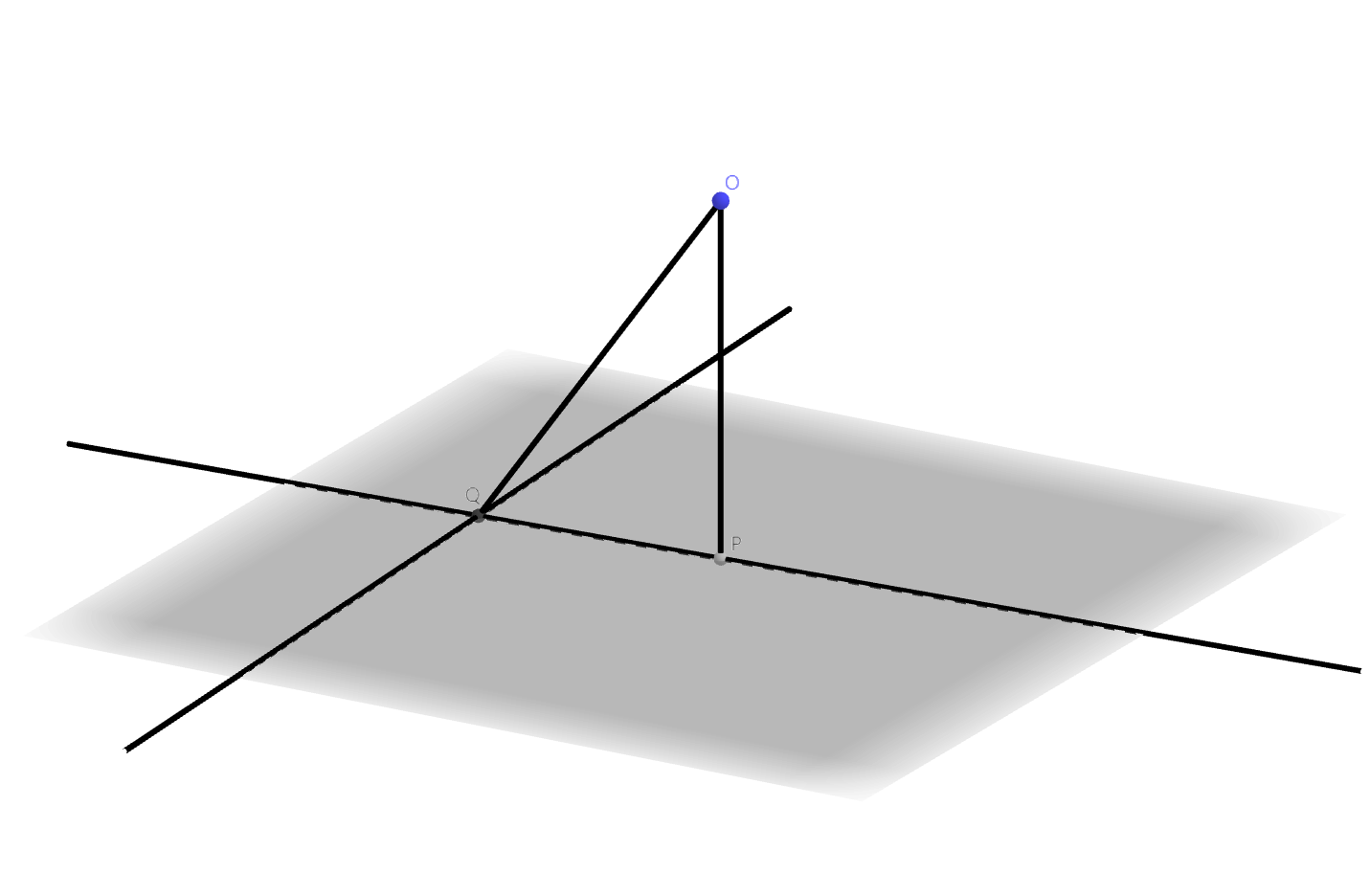
过点$O$作平面$\alpha$的唯一垂线，垂足为$P$，则线段$OP$称为点$O$到平面$\alpha$的垂线段（perpendicular line segment），垂线段的长度$|OP|$称为点$O$到平面$\alpha$的距离（distance from a point to a plane）。
$OQ$所在的直线与平面$\alpha$相交但不垂直，称为平面$\alpha$的斜线，交点$Q$称为斜足。$\angle OQP$称为直线$OQ$与平面$\alpha$所成的角。平面与其平行线所成的角是$0$，平面与其垂线所成的角是$\dfrac{\pi}{2}$，因此，直线与平面所成的角范围是$[0, \dfrac{\pi}{2}]$。
直线$PQ$称为直线$OQ$在平面$\alpha$内的射影（projection）。

从上面存在性的证明得到启发，有三垂线定理：
平面内的直线与斜线垂直的充要条件是：该直线与斜线的射影垂直。

由三垂线定理可以得到三余弦定理：
平面内一条直线与该平面一条斜线夹角的余弦值，等于斜线与平面所成的角的余弦值，乘以平面内直线与斜线射影的夹角的余弦值。

如图，$OA \subset \alpha$，$OC$为斜线$OB$在平面$\alpha$的射影，三余弦定理有

$$\cos \angle AOB = \cos \angle AOC \cos \angle BOC$$

下面是直线与平面垂直的性质：
垂直于同一平面的两条直线平行。
用形式化的语言表示就是：

$$m \perp \alpha, n \perp \alpha \Rightarrow m \parallel n$$

用反证法可以证明：
假设$m \nparallel n$。设$n \cap \alpha = P$，作直线$m’$过点$P$且有$m’ \parallel m$，则$m’ \cap n = P$。设$m’, n$确定平面$\beta$，$\alpha \cap \beta = l$。此时有$m’ \perp l, n \perp l$，且$m’, n, l \subset \beta$，得到$m’ \parallel n$，矛盾。$\Box$

平面与平面垂直

一条直线把平面分成两部分，每一部分都叫做一个半平面（half-plane），直线叫做半平面的边界。一条直线与以它为边界的两个半平面组成了一个二面角（dihedral angle）。这条直线叫做二面角的棱，两个半平面叫做二面角的面。棱为$l$，面分别为$\alpha, \beta$的二面角记作$\alpha-l-\beta$；也可在半平面$\alpha, \beta$内分别取点$P, Q$，棱用$AB$来表示，记作$P-AB-Q$。
在二面角$\alpha-l-\beta$的棱$l$上任取一点$O$，在半平面$\alpha, \beta$内分别作射线$OA \perp l, OB \perp l$，则$\angle AOB$称为二面角的平面角。二面角的大小就是其平面角的大小，取值范围是$[0, \pi]$。
两个平行的平面所成的二面角大小规定为$0$。大小为$\dfrac{\pi}{2}$的二面角称为直二面角，此时两个平面垂直。平面$\alpha, \beta$垂直，记为$\alpha \perp \beta$。

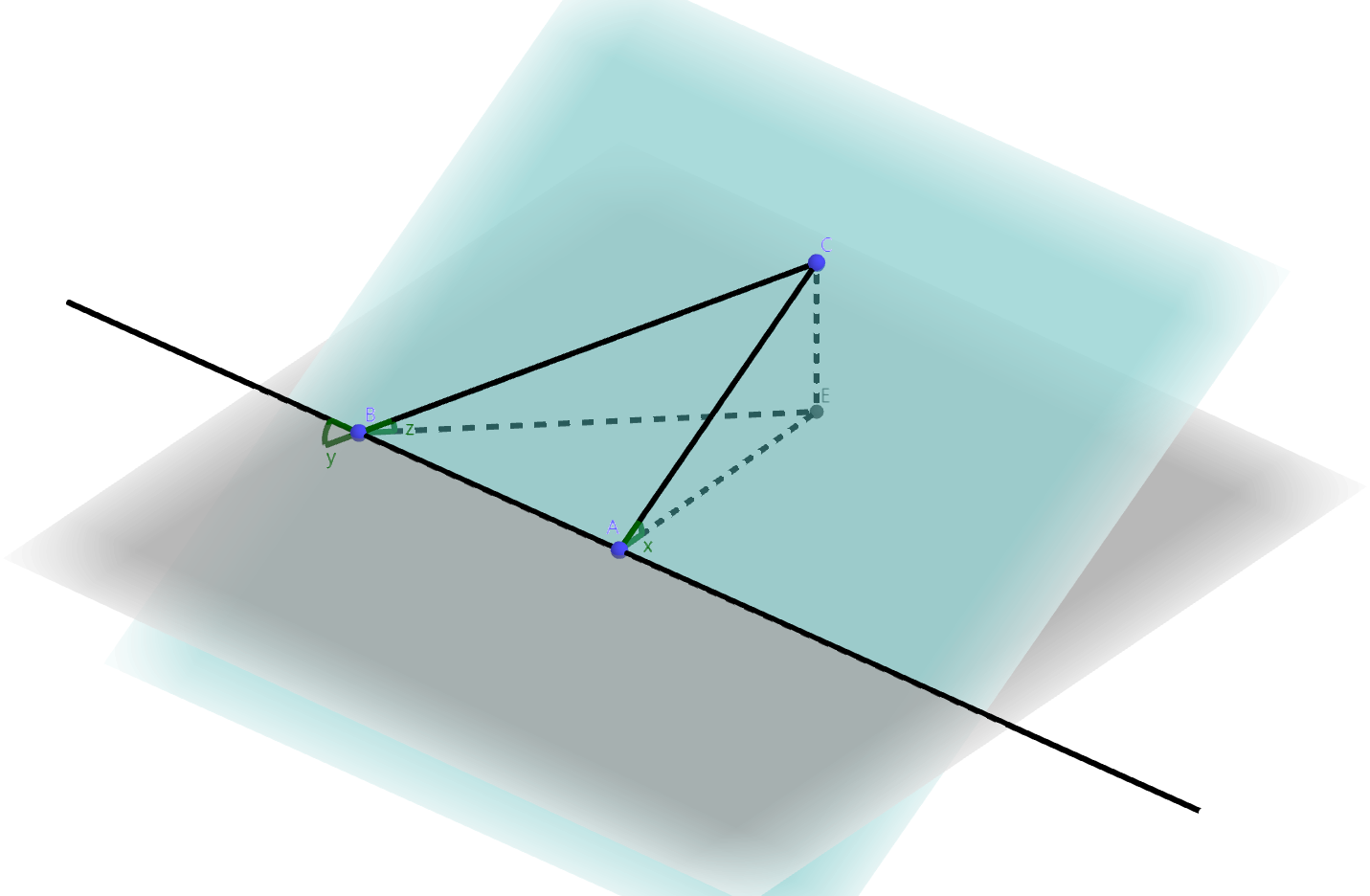
解直角三角形可以得到三正弦定理：
设二面角$\alpha-l-\beta$的大小为$x$，半平面$\alpha$上一条直线与$l$的夹角为$y$，与平面$\beta$所成的角为$z$，则有

$$\sin z = \sin x \sin y$$

对于平面与平面的垂直关系，有判定定理：
若一个平面过另一个平面的垂线，则这两个平面垂直。
用形式化的语言表示就是：

$$l \perp \beta, l \subset \alpha \Rightarrow \alpha \perp \beta$$

证明：
设$\alpha \cap \beta = m$，则$m \subset \beta$。由$l \perp \beta$，得到$l \perp m$。设$l \perp m = O$，过$O$在平面$\beta$内作$m$的垂线$n$。由$l \perp \beta$，得到$l \perp n$。此时$l, n$的夹角是$\dfrac{\pi}{2}$，即二面角$\alpha-m-\beta$的大小。$\Box$

对于平面与平面的垂直关系，有性质定理：
两个平面垂直，若一个平面内有一条直线垂直于这两个平面的交线，则这条直线垂直于另一个平面。
用形式化的语言表示就是：

$$\alpha \perp \beta, \alpha \cap \beta = l, a \subset \alpha, a \perp l \Rightarrow a \perp \beta$$

证明：
设$a \cap l = P$，过点$P$在平面$\beta$内作$l$的垂线$b$。这样$a, b$的夹角即二面角的大小$\dfrac{\pi}{2}$，$a \perp b$。而$a \perp l, l \cap b = P, l \subset \beta, b \subset \beta$，故$a \perp \beta$。$\Box$

几何体

基本几何体

多面体

多面体（polyhedron）是边界由若干个平面多边形组成的几何体。这些多边形叫做多面体的面（face），面的公共边叫做多面体的棱（edge），棱的公共点叫做多面体的顶点（vertex）。
有公共点的$n (n \ge 3)$条射线，以及相邻两条射线之间的平面，构成了一个多面角。这些射线叫做多面角的棱，公共点叫做多面角的顶点，平面叫做多面角的面。有$n$条棱的多面角称为$n$面角。相邻两条棱的夹角叫做多面角的平面角，相邻两个平面的夹角叫做多面角的二面角。
如果多面体的所有面都是全等的正多边形，并且所有多面角都全等，那么这样的多面体称为正多面体（regular polyhedron）。正多面体只有5种：正四面体（regular tetrahedron）、正六面体（正方体，cube）、正八面体（regular octahedron）、正十二面体（regular dodecahedron）、正二十面体（regular icosahedron）。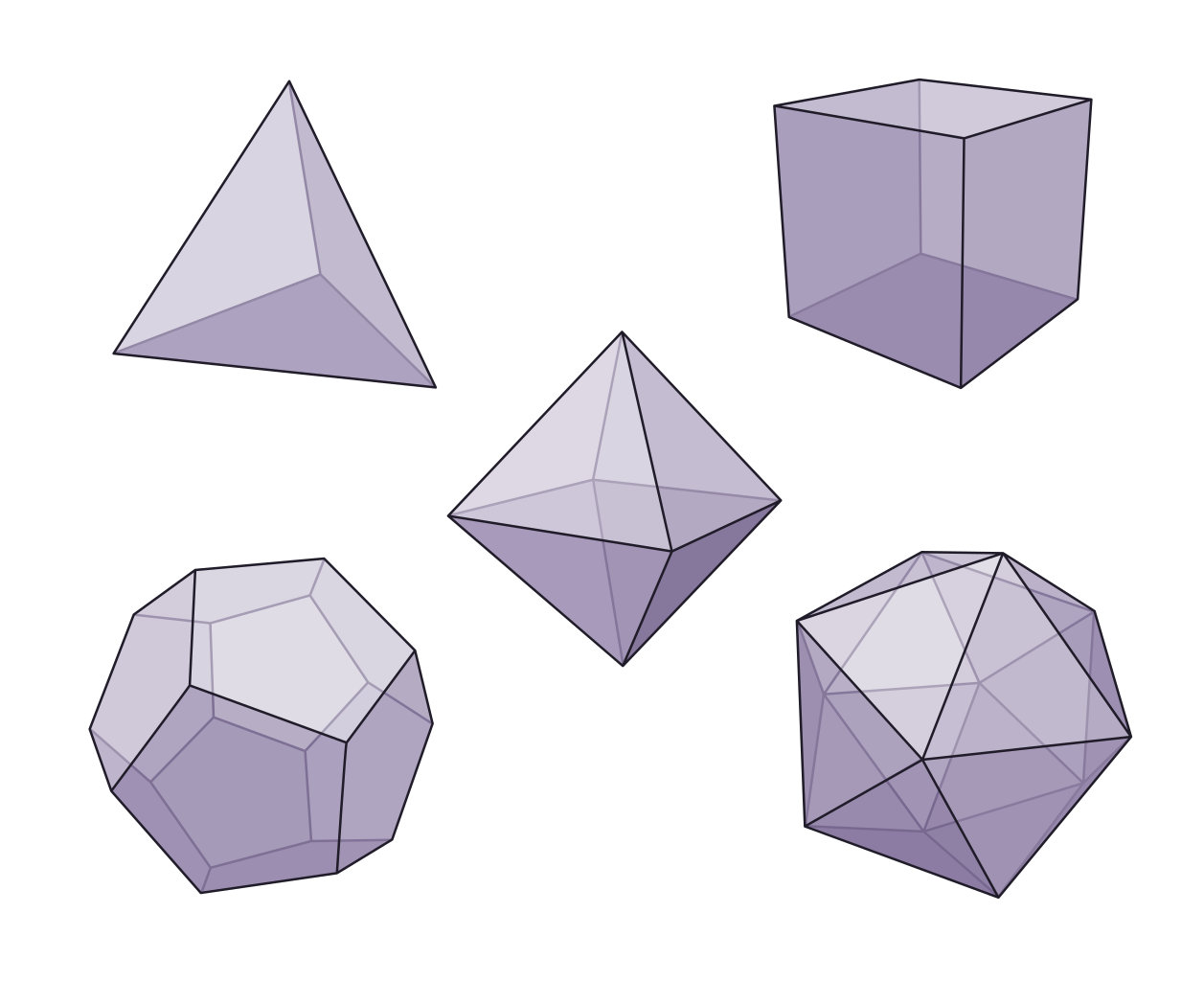

棱柱（prism）是有两个面平行且全等，其余各面都是四边形，并且这些四边形的公共边都互相平行的多面体。两个平行的面叫做棱柱的底面（base），其余各面叫做棱柱的侧面，侧面的公共边叫做棱柱的侧棱。
侧棱垂直于底面的棱柱称为直棱柱（right prism），否则称为斜棱柱（oblique prism）。
底面为$n$边形的棱柱叫做$n$棱柱（n-gonal prism），底面为正$n$边形的棱柱叫做正$n$棱柱（regular n-gonal prism）。底面为平行四边形的棱柱又叫平行六面体（parallelepiped）。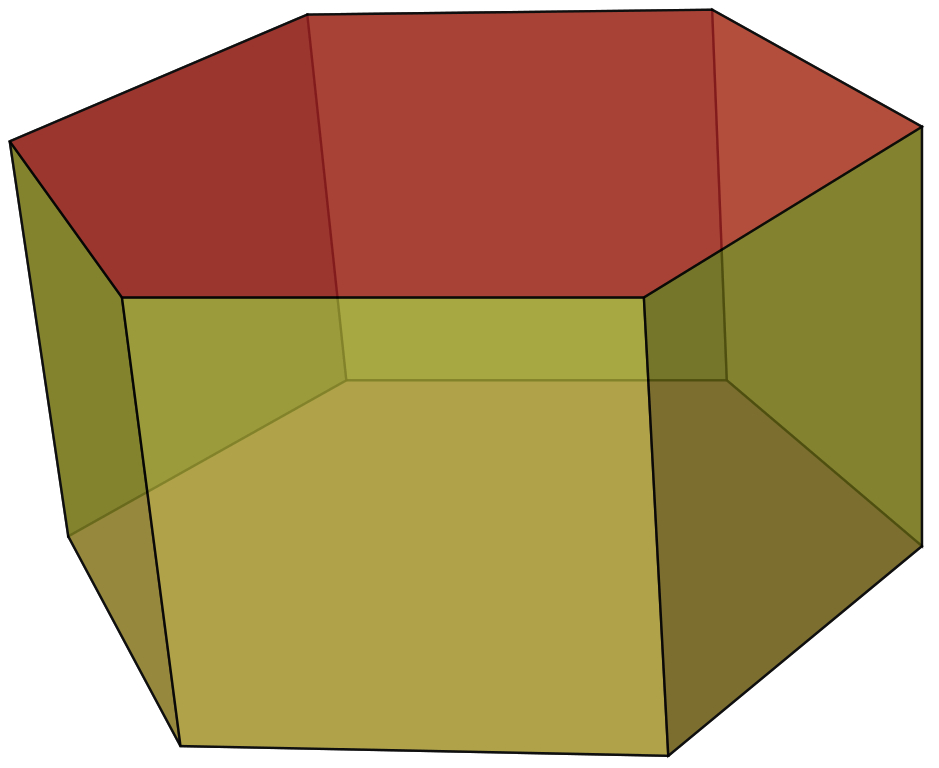


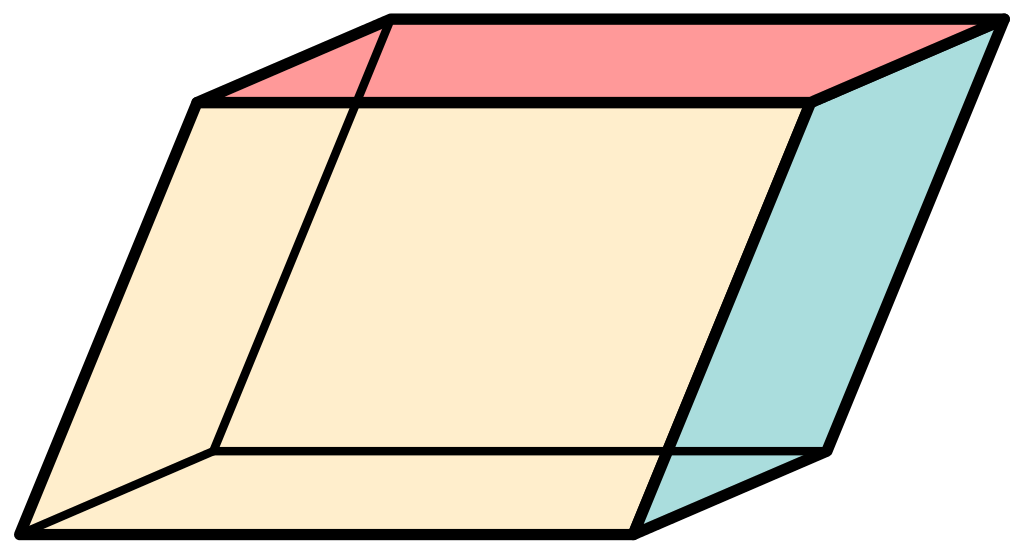
棱柱用底面来表示。设棱柱的两个底面分别是$n$边形$A_{1} A_{2} \cdots A_{n}, B_{1} B_{2} \cdots B_{n}$，其中$A_{k}, B_{k}$之间有侧棱连接，则棱柱表示为$A_{1} A_{2} \cdots A_{n}-B_{1} B_{2} \cdots B_{n}$。

棱锥（pyramid）是多面角被一个平面所截得到的多面体。平面被多面角截得的面叫做棱锥的底面（base），其余各面叫做棱锥的侧面，侧面的公共边叫做棱锥的侧棱，多面角的顶点叫做棱锥的顶点（apex）。
底面为$n$边形的棱锥叫做$n$棱锥（n-gonal pyramid），底面为正$n$边形且顶点与底面中心的连线垂直于底面的棱锥叫做正$n$棱锥（regular n-gonal pyramid）。底面为三角形的棱锥又叫四面体（tetrahedron），所有棱长相等的四面体叫做正四面体。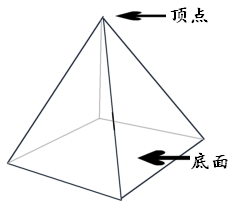

棱锥用顶点和底面来表示。设棱锥的顶点是$P$，底面是$n$边形$A_{1} A_{2} \cdots A_{n}$，则棱锥表示为$P-A_{1} A_{2} \cdots A_{n}$。四面体的四个顶点都可以作为棱锥的顶点，所以设四个顶点是$A, B, C, D$，四面体也可以记为$ABCD$。

棱台（frustum）是用平行于棱锥底面的平面截棱锥，所得的底面与截面之间的部分。原棱锥的底面和截面分别叫做棱台的下底面和上底面，原棱锥的侧面截得的部分叫做棱台的侧面，原棱锥的侧棱截得的部分叫做棱台的侧棱。
底面和截面为$n$边形的棱台叫做$n$棱台（n-gonal frustum）。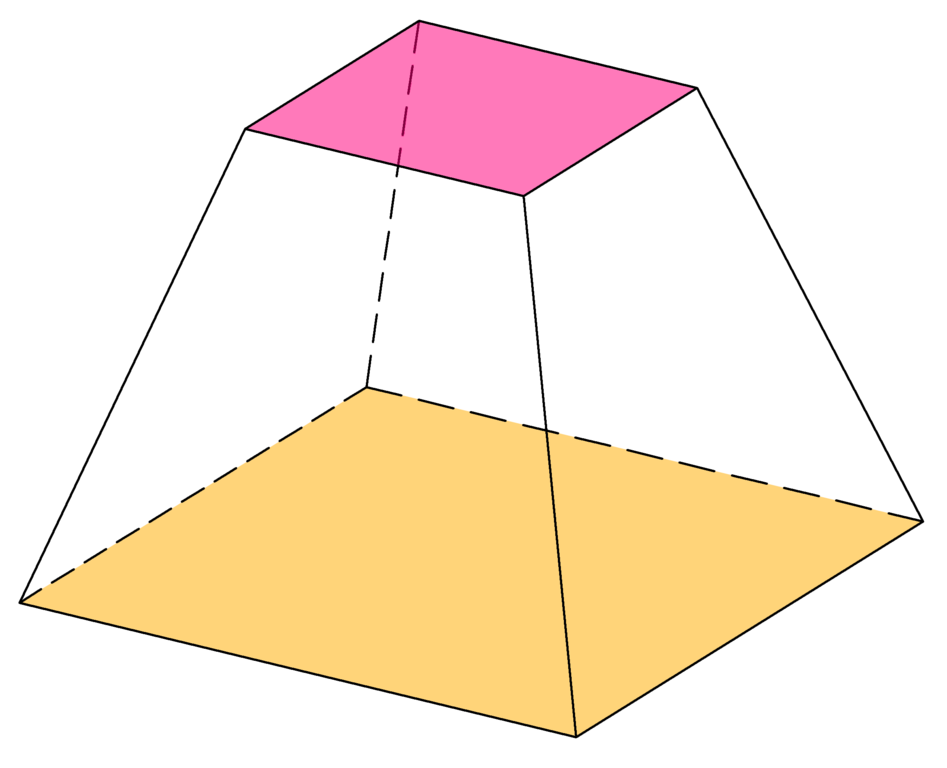

棱台和棱柱一样，用底面来表示。

旋转体

旋转体（solid of revolution）是平面图形绕同一平面内的一条直线旋转一周形成的几何体。这条直线叫做旋转体的轴（axis）。

圆柱（cylinder）是矩形绕其一边旋转一周形成的旋转体。垂直于轴的边旋转而成的圆面叫做圆柱的底面，平行于轴的边旋转而成的曲面叫做圆柱的侧面，这条平行于轴的边旋转得到的任何线段都叫做圆柱的母线（generatrix）。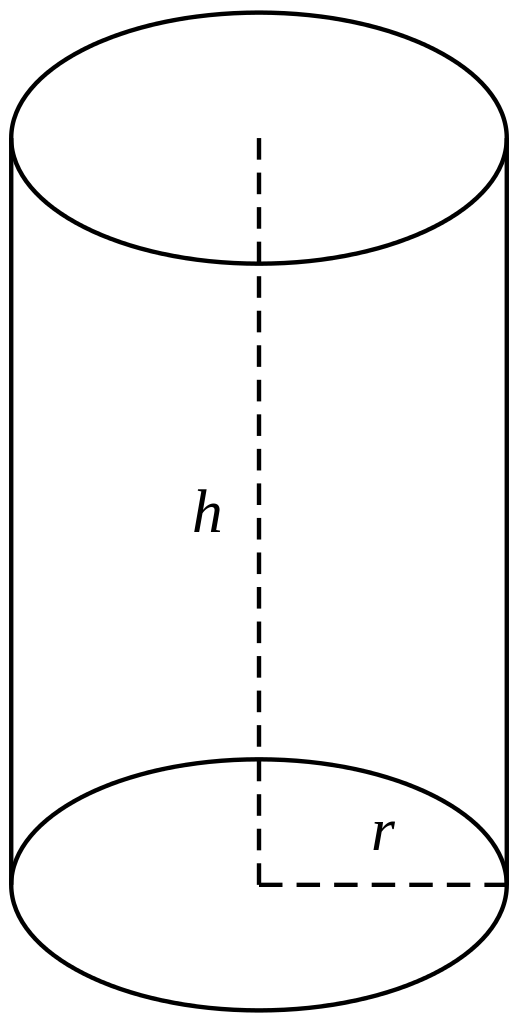

圆柱用底面的圆心来表示。设圆柱底面的圆心是$O_{1}, O_{2}$，则圆柱表示为$O_{1} O_{2}$。

圆柱和棱柱都属于柱体。柱体是一个平面图形沿某一不在平面内的方向平移得到的几何体。如果这个方向与平面垂直，那么称为直柱体，否则称为斜柱体。两个底面之间的垂线段叫做柱体的高（height），圆柱的母线和高等长。

圆锥（cone）是直角三角形绕其一直角边旋转一周形成的旋转体。轴的非直角顶点叫做圆锥的顶点，另一条直角边旋转而成的圆面叫做圆锥的底面，斜边旋转而成的曲面叫做圆锥的侧面，斜边旋转得到的任何线段都叫做圆锥的母线。作为圆锥的轴的直角边叫做圆锥的高，圆锥的高与底面垂直。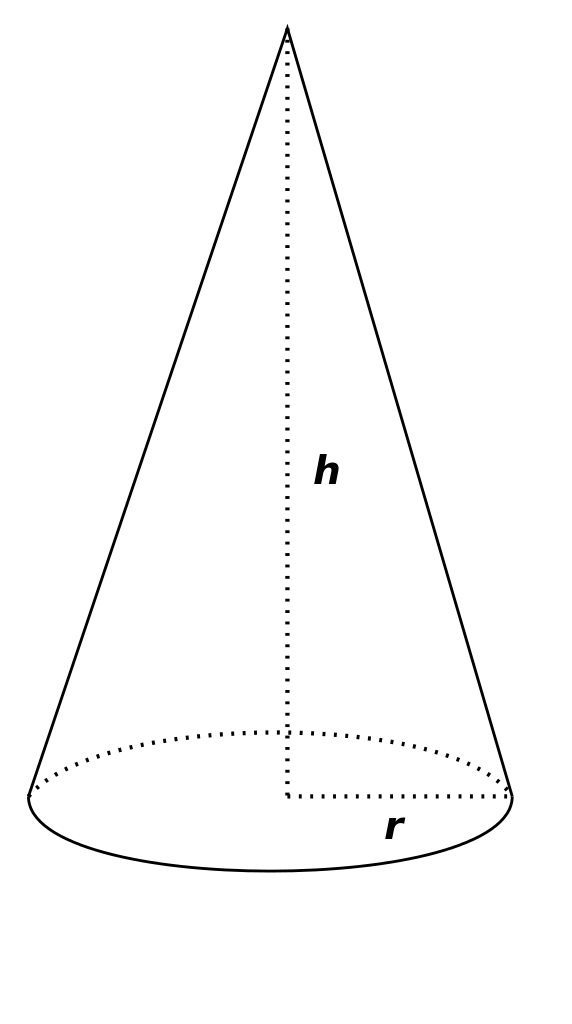

圆锥用顶点和底面圆心来表示。设圆锥的顶点是$S$，底面的圆心是$O$，则圆锥表示为$SO$。

圆锥和棱锥都属于锥体。锥体是一个平面图形上的点与平面外一点所连线段的并集。过这一点的平面的垂线叫做锥体的高。

圆台（truncated cone）是用平行于圆锥底面的平面截圆锥，所得的底面与截面之间的部分。原圆锥的底面和截面分别叫做圆台的下底面和上底面，原圆锥的侧面截得的部分叫做圆台的侧面，原圆锥的母线截得的部分叫做圆台的母线。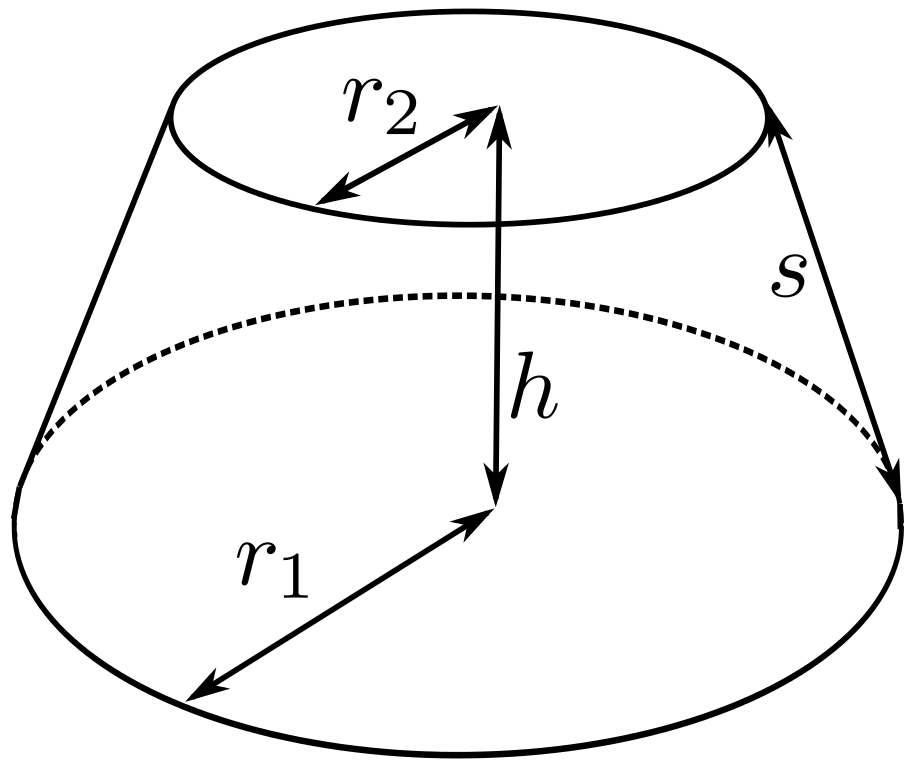

圆台和圆柱一样，用底面的圆心来表示。

圆台的棱台都属于台体。台体是一个锥体被平行于锥体底面的平面所截，所得的底面与截面之间的部分。两个底面之间的垂线段叫做台体的高。

球（ball）是半圆绕其直径旋转一周形成的旋转体。半圆的圆心叫做球的球心（center），连接球心和球面上任意一点的线段叫做球的半径（radius）。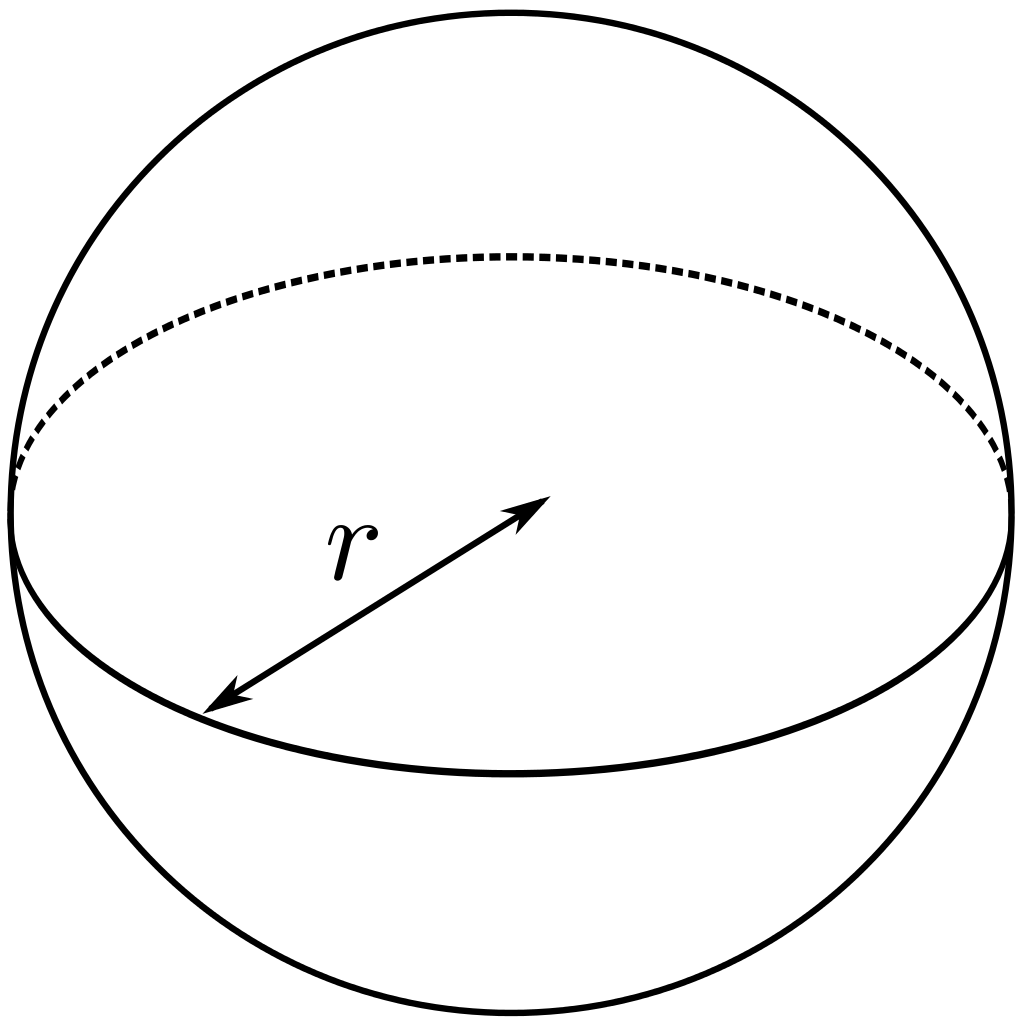

球用球心表示。设球的球心是$O$，则球表示为$O$。

一个与球内部相交的平面把球分为两部分，每个部分都叫做球缺（spherical cap）。截面叫做球缺的底面，球面与底面的最远距离叫做球缺的高。

几何体的表面积和体积

祖暅原理与体积公式

三国时期，魏国数学家刘徽（约225—约295）发现了《九章算术》中的一个错误：球的体积是同等高度和底面半径的圆柱体积的$\dfrac{3}{4}$。刘徽在一个正方体中内切两个垂直的圆柱，取这两个圆柱的交集，构造出一个几何体，他称为“牟合方盖”。刘徽发现，球的体积是对应的牟合方盖的$\dfrac{3}{4}$，而牟合方盖的体积又比圆柱小，因此《九章算术》给出的球的体积一定是错误的。只要能算出牟合方盖的体积，就能得到球的体积。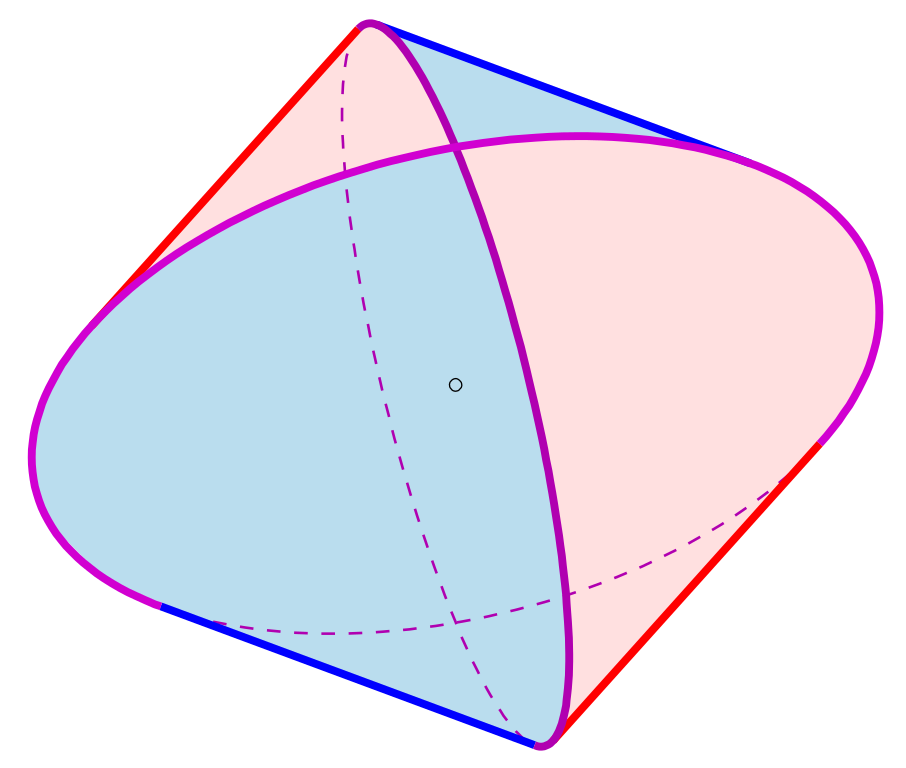

不过，刘徽始终没能算出牟合方盖的体积。直到南北朝时期，祖冲之的儿子祖暅计算出了牟合方盖的体积，进而得到了导出各种几何体体积的通法，这就是祖暅原理：
幂势既同，则积不容异。

其含义是：
夹在两个平行平面之间的两个几何体，被平行于这两个平行平面的平面所截，若截得的两个截面积总是相等，则这两个几何体体积相等。

祖暅原理在17世纪由意大利数学家卡瓦列里（Bonaventura Cavalieri，1598—1647）重新发现，因此在西方被称为卡瓦列里原理（Cavalieri’s principle）。这个原理需要用到微积分才能解释。

首先，我们知道三条棱长为$a, b, c$的长方体体积公式为：

$$V = abc$$

设柱体底面积为$S$，高为$h$，利用祖暅原理，作与柱体的底面积和高都相等的长方体，就能得到一般的柱体体积公式：

$$V = Sh$$

由祖暅原理可得，所有底面积和高相等的锥体体积相等。那么，只要得到三棱锥的体积公式，就能作与锥体的底面积和高都相等的三棱锥，从而得到一般的锥体体积公式。
如图，已知三棱锥$D-ABC$，设其体积为$V$。过点$D$作平面$\alpha$平行于平面$ABC$，并分别过$B, C$作$AD$的平行线，交$\alpha$于点$E, F$。这样得到三棱柱$ABC-DEF$。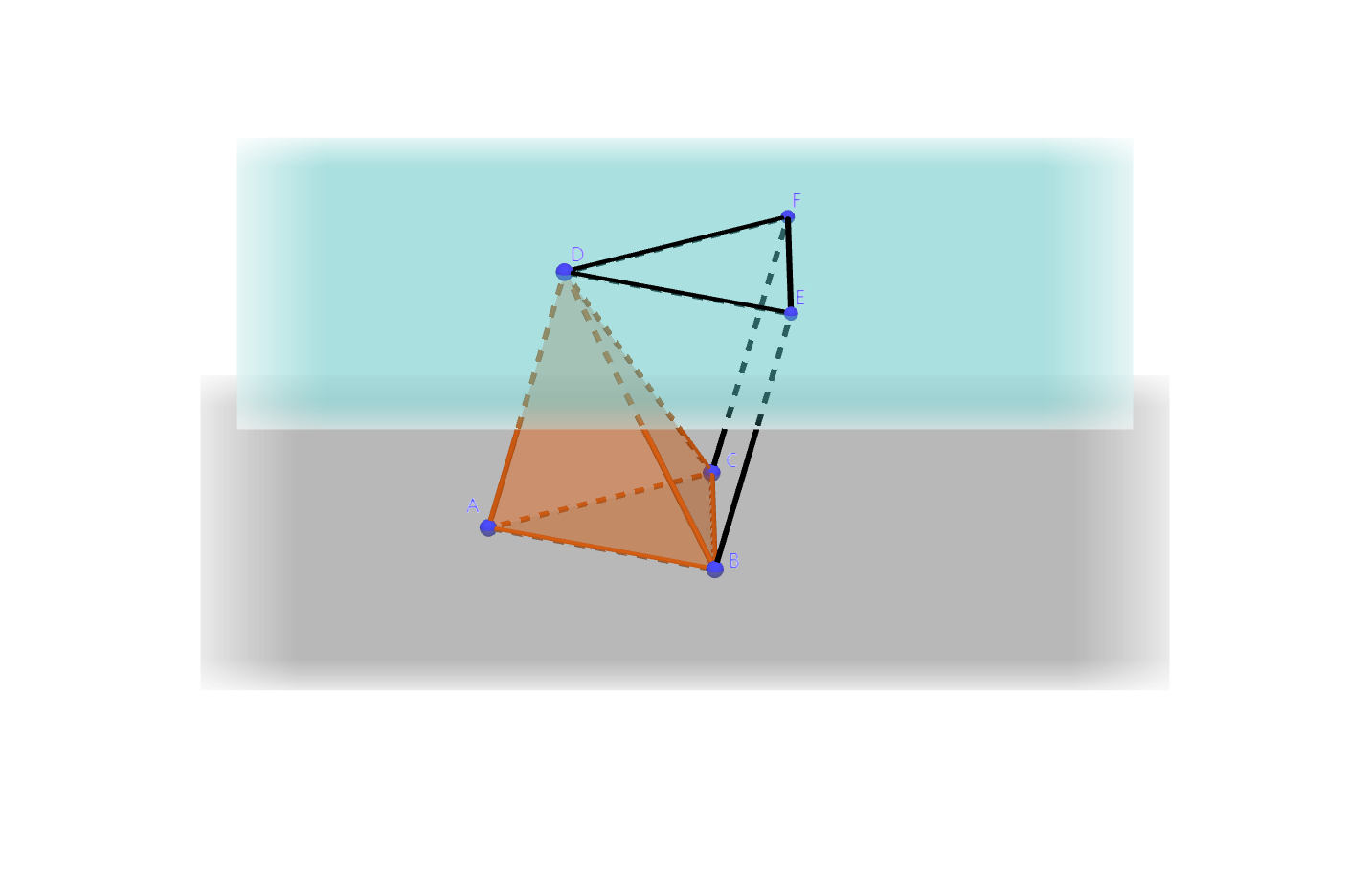

三棱柱的体积是$Sh$，而三棱柱又由$D-ABC, B-DEF, B-CDF$三个三棱锥组成，所以$Sh = V + V_{B-DEF} + V_{B-CDF}$。因为$\triangle ABC \cong \triangle DEF$，所以$B-DEF, D-ABC$的底面积和高相等，$V_{B-DEF} = V$；因为$ACFD$是平行四边形，所以$\triangle CDF \cong \triangle DCA$，三棱锥$D-ABC$也可以写成$B-DCA$，$B-CDF, B-DCA$的底面积和高相等，$V_{B-CDF} = V$。代入得$Sh = 3V$，这样就得到锥体体积公式：

$$V = \dfrac{1}{3} Sh$$

台体的体积可以通过转化为锥体来解决。设台体的两个底面积为$S, S’$，高为$h$。如图，已知三棱台$ABC-DEF$，不妨设$S’ < S$，沿$S’$方向延长侧棱，交于一点$G$，得到三棱锥$G-ABC$。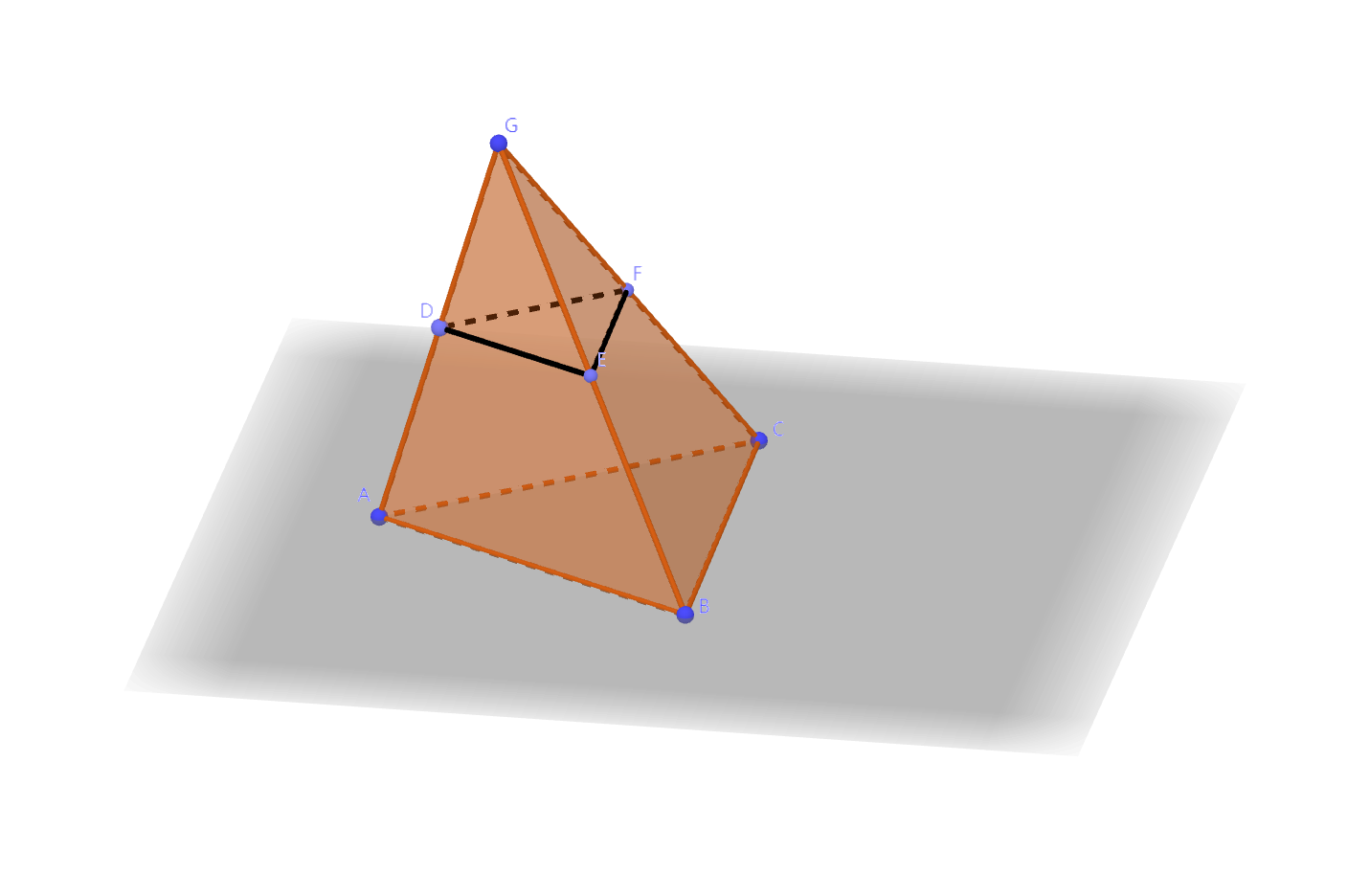

两个底面图形相似，上下底面相似比为$k = \sqrt{\dfrac{S’}{S}}$。设点$G$到上、下底面的距离分别是$h_{1}, h_{2}$，则$h_{1} = kh_{2}, h = h_{2} - h_{1}$，从而得到$h_{2} = \dfrac{1}{1 - k} h, h_{1} = \dfrac{k}{1 - k} h$。
根据锥体体积公式，

$$\begin{align} V &= \dfrac{1}{3} (Sh_{2} - S'h_{1}) \\ &= \dfrac{1}{3 (1 - k)} (S - kS') h \\ &= \dfrac{1}{3} (\dfrac{\sqrt{S^{3}} - \sqrt{S'^{3}}}{\sqrt{S} - \sqrt{S'}}) h \\ &= \dfrac{1}{3} (S + \sqrt{SS'} + S') h \end{align}$$

于是，台体体积公式：

$$V = \dfrac{1}{3} (S + \sqrt{SS'} + S') h$$

特别地，圆柱、圆锥、圆台体积公式分别为：

$$\begin{align} & V = \pi r^{2} h \\ & V = \dfrac{1}{3} \pi r^{2} h \\ & V = \dfrac{1}{3} \pi (r_{1}^{2} + r_{1} r_{2} + r_{2}^{2}) h \end{align}$$

其中，$r$是圆柱、圆锥的底面半径，$r_{1}, r_{2}$是圆台的两个底面的半径。

圆柱、圆锥、圆台的表面积公式

圆柱、圆锥、圆台的底面都是圆，所以问题主要是侧面积的计算。我们可以通过展开图（net）来计算侧面的面积。

圆柱侧面的展开图是一个矩形，一条边长是底面的周长$2 \pi r$，另一条边长是圆柱的高$h$，因此加上两个底面的圆，就得到圆柱表面积公式：

$$S = 2 \pi r (r + h)$$

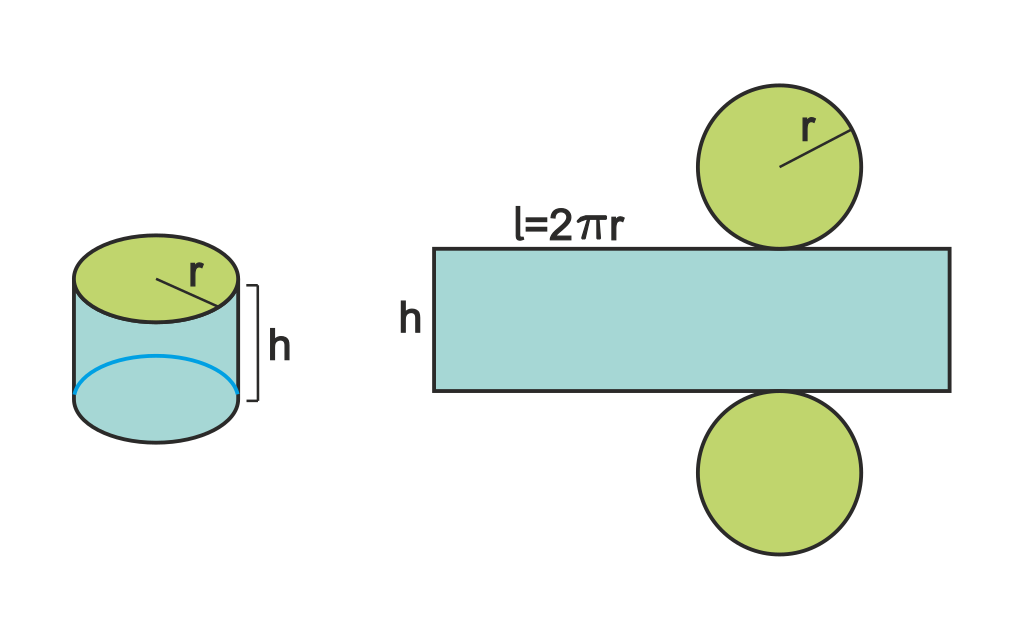
圆锥侧面的展开图是一个扇形，半径是母线长$l$，弧长是底面的周长$2 \pi r$，所以圆锥表面积公式是：

$$S = \pi r (r + l)$$

圆台侧面的展开图是一个扇环，内外半径差是母线长$l$，内、外弧长分别是两个底面的周长$2 \pi r_{1}, 2 \pi r_{2}$，所以圆台表面积公式是：

$$S = \pi (r_{1}^{2} + r_{2}^{2} + r_{1} l + r_{2} l)$$

球的表面积和体积公式

前面提到，刘徽用牟合方盖给出了计算球的体积的方法。而在刘徽之前，古希腊数学家阿基米德（Archimedes，约前287—约前212）用另一种方法算出了球的体积：

$$V = \dfrac{4}{3} \pi r^{3}$$

其中$r$是球的半径。

接下来用阿基米德的方法来证明：
设球的体积为$V$，半径为$r$。如图，构造一个底面半径和高都等于$r$的圆柱，并挖去一个圆锥。平面$\alpha$经过球的球心和圆柱的底面与圆锥的顶点。

首先，平面$\alpha$上面的半球和圆柱的底面积相等。然后任意作一个与平面$\alpha$平行的平面$\beta$截半球和右边的几何体，设$\alpha$与$\beta$的距离为$d$。截面和半球相交得到一个圆，半径为$\sqrt{r^{2} - d^{2}}$，所以面积为$\pi (r^{2} - d^{2})$；右边的几何体截面是一个圆环，内半径由相似关系得到是$d$，外半径是$r$，所以圆环面积为$\pi (r^{2} - d^{2})$。这样，两者截面积总是相等，根据祖暅原理，半球和右边的几何体体积相等。而这个几何体的体积可以直接计算：

$$\dfrac{1}{2} V = \pi r^{2} \cdot r - \dfrac{1}{3} \pi r^{2} \cdot r = \dfrac{2}{3} \pi r^{3}$$

于是得到球的体积$V = \dfrac{4}{3} \pi r^{3}$。$\Box$

球的表面积公式是：

$$S = 4 \pi r^{2}$$

可以通过细分球面的方法来证明：
如图，把球面按照经纬线的方式分成很多小块，设有$n$块，每块面积为$S_{i}$，则$\sum\limits_{i=1}^{n} S_{i} = S$。

如果每块足够小，那就可以近似地看为锥体，所以$V_{i} \approx \dfrac{1}{3} r S_{i}$，从而

$$V \approx \sum\limits_{i=1}^{n} V_{i} = \dfrac{1}{3} r \sum\limits_{i=1}^{n} S_{i} = \dfrac{1}{3} r S$$

当$n$趋于无穷大时，误差趋于$0$，所以$V = \dfrac{1}{3} r S = \dfrac{4}{3} \pi r^{3}$，得到$S = 4 \pi r^{2}$。$\Box$

球

球也可以定义为空间中到一个定点距离不大于定长的点的集合，是圆在三维空间中的推广，因此也有一些重要的性质。

平面几何中，不共线的三点唯一确定一个圆。类似地：
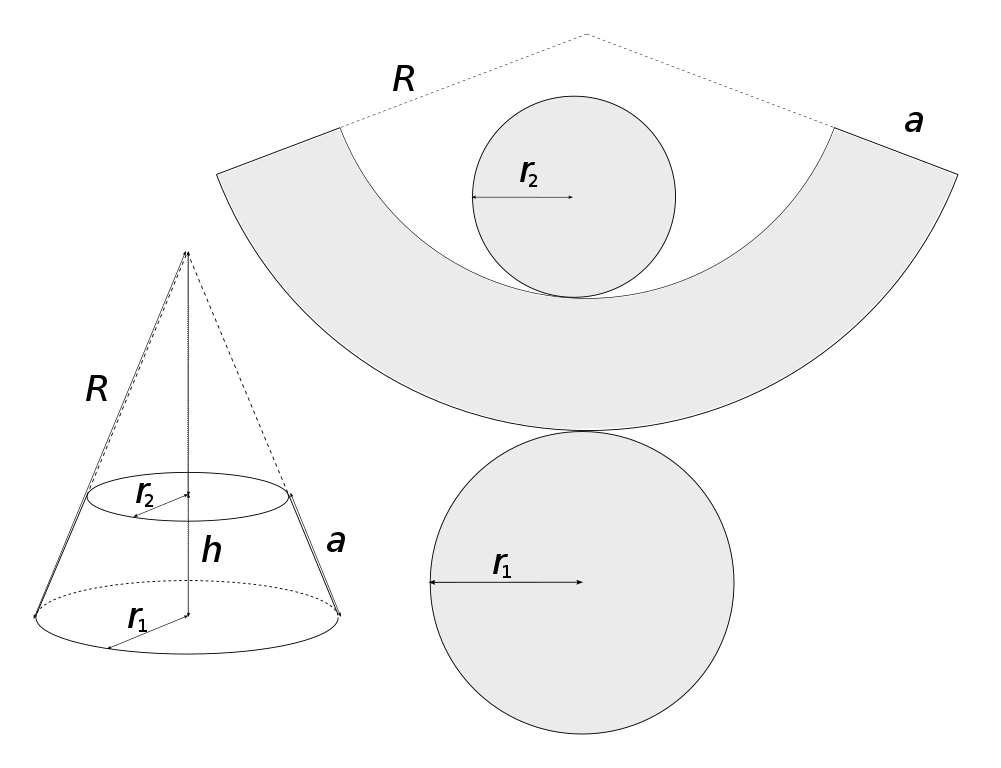
不共面的四点唯一确定一个球。

证明：
存在性：如图，$A, B, C, D$四点不共面，设$\triangle ABC$的外心是$O_{1}$，$\triangle DBC$的外心是$O_{2}$，$BC$中点是$E$。在平面$O_{1}O_{2}E$内作两条直线$OO_{1} \perp O_{1}E, OO_{2} \perp O_{2}E$，两线交于点$O$。因为$O_{1}, O_{2}$是外心，所以$O_{1}E \perp BC, O_{2} \perp BC$，得到$BC \perp$平面$O_{1}O_{2}E$。
$OO_{1} \subset$平面$O_{1}O_{2}E$，所以$BC \perp OO_{1}$，又$BC \perp O_{1}E, BC \cap O_{1}E = E$，且$BC, O_{1}E \subset$平面$ABC$，所以$OO_{1} \perp$平面$ABC$。由$|O_{1}A| = |O_{1}B| = |O_{1}C|$可证得全等三角形，故$|OA| = |OB| = |OC|$，同理$|OD| = |OB| = |OC|$。这样就有$|OA| = |OB| = |OC| = |OD|$，得到球$O$。

唯一性：$A, B, C, D$四点确定的球心，是由四个三角形$ABC, BCD, CDA, DAB$的外心引出的与各自平面垂直的直线交点。因为两点唯一确定一条直线，所以这样的点至多只有一个。$\Box$

这个球也叫四面体$ABCD$的外接球（circumscribed sphere），球心$O$叫做四面体的外心。

球被一个平面所截，如果球与平面没有交点，那么称球与平面相离；如果恰有一个交点，那么称球与平面相切，交点称为切点；如果至少有两个交点，那么称球与平面相交。球被平面所截，还有一个显而易见的重要性质：
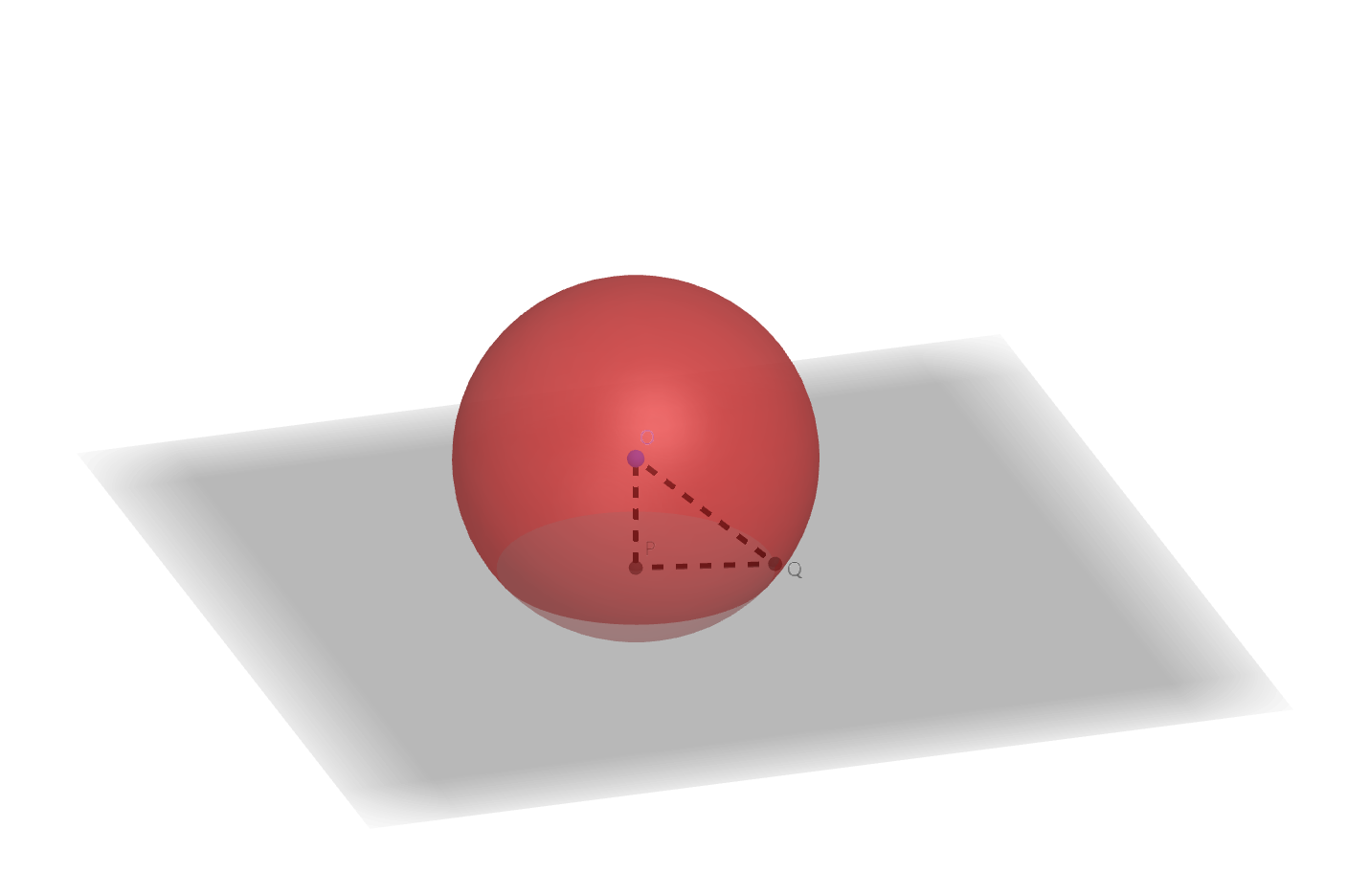
球体被任何平面所截，截面是一个圆。

证明：
如图，设球$O$被平面$\alpha$所截，球面与平面$\alpha$的交集为曲线$C$。作$OP \perp \alpha$，垂足为$P$，并取$Q \in C$。因为$PQ \subset \alpha$，所以$OP \perp PQ$，由勾股定理知道$|PQ| = \sqrt{|OQ|^{2} - |OP|^{2}} = \sqrt{r^{2} - |OP|^{2}}$为定值。因此$C$的点都在一个圆心为$P$，半径为$d = \sqrt{r^{2} - |OP|^{2}}$的圆$\gamma$上。
任取点$R \in \gamma$，则$|PR| = d$。而$OP \perp PR$，由勾股定理知道$|OR| = \sqrt{d^{2} + |OP|^{2}} = r$，所以$R$在球面上，也就是圆$\gamma$的点都在$C$上。由此得到$C$就是圆$\gamma$。$\Box$

球体被平面所截得到的圆有两种：经过圆心的圆称为大圆（great circle），不经过圆心的圆称为小圆（small circle）。大圆是所有截面圆中半径最大的。
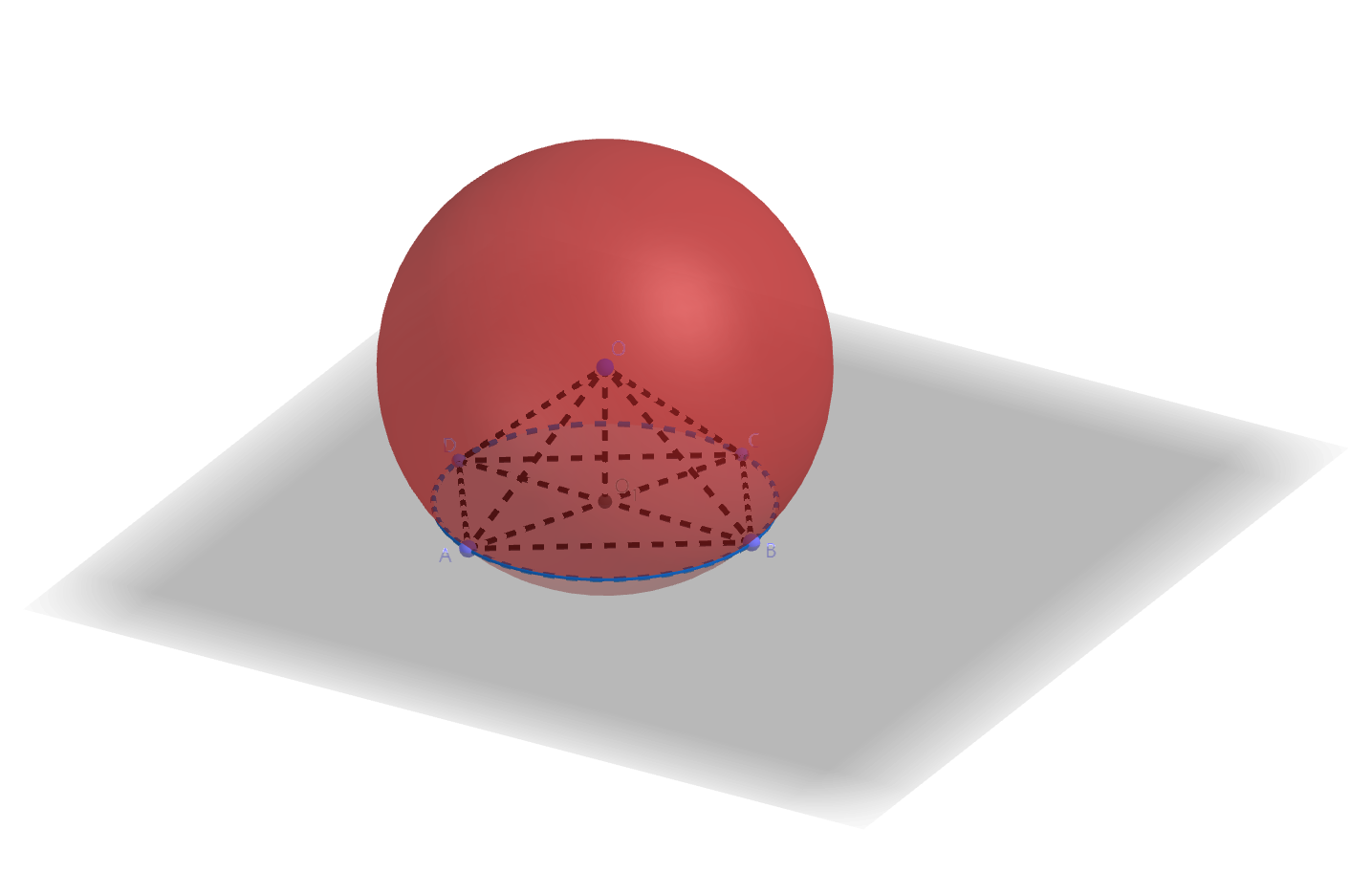
设球$O$的一个小圆为圆$O_{1}$，则$OO_{1}$垂直于圆$O_{1}$所在平面。

证明：
作圆$O_{1}$的内接矩形$ABCD$，则$O_{1}$为$AC, BD$中点。因为$|OA| = |OC|$，所以$\triangle OO_{1}A \cong \triangle OO_{1}C$。所以$\angle OO_{1}A = \angle OO_{1}C = \dfrac{\pi}{2}$，得到$OO_{1} \perp AC$，同理$OO_{1} \perp BD$。又$AC \cap BD = O_{1}$，所以$OO_{1} \perp$平面$ABCD$。$\Box$

类似地，有相切关系的定理：
设球$O$与平面$\alpha$相切，切点为$P$，则$OP \perp \alpha$；
设球$O$与直线$l$相切，切点为$P$，则$OP \perp l$。

在平面几何中，有圆的相交弦定理、切割线定理和割线定理，这三条定理都来源于圆幂定理。而在立体几何中，也有相应的球幂定理。
设球$O$的半径是$r$，$P$为空间中一点，我们称$|OP|^{2} - r^{2}$的绝对值为点$P$关于球$O$的幂：
设$P$是不在球$O$的球面上的点，过点$P$作直线$l$与球面交于两点$A, B$，则$|PA| \cdot |PB|$等于点$P$关于球$O$的幂；
设$P$是不在球$O$的球面上的点，过点$P$作直线$l$与球面相切于点$T$，则$|PT|^{2}$等于点$P$关于球$O$的幂。

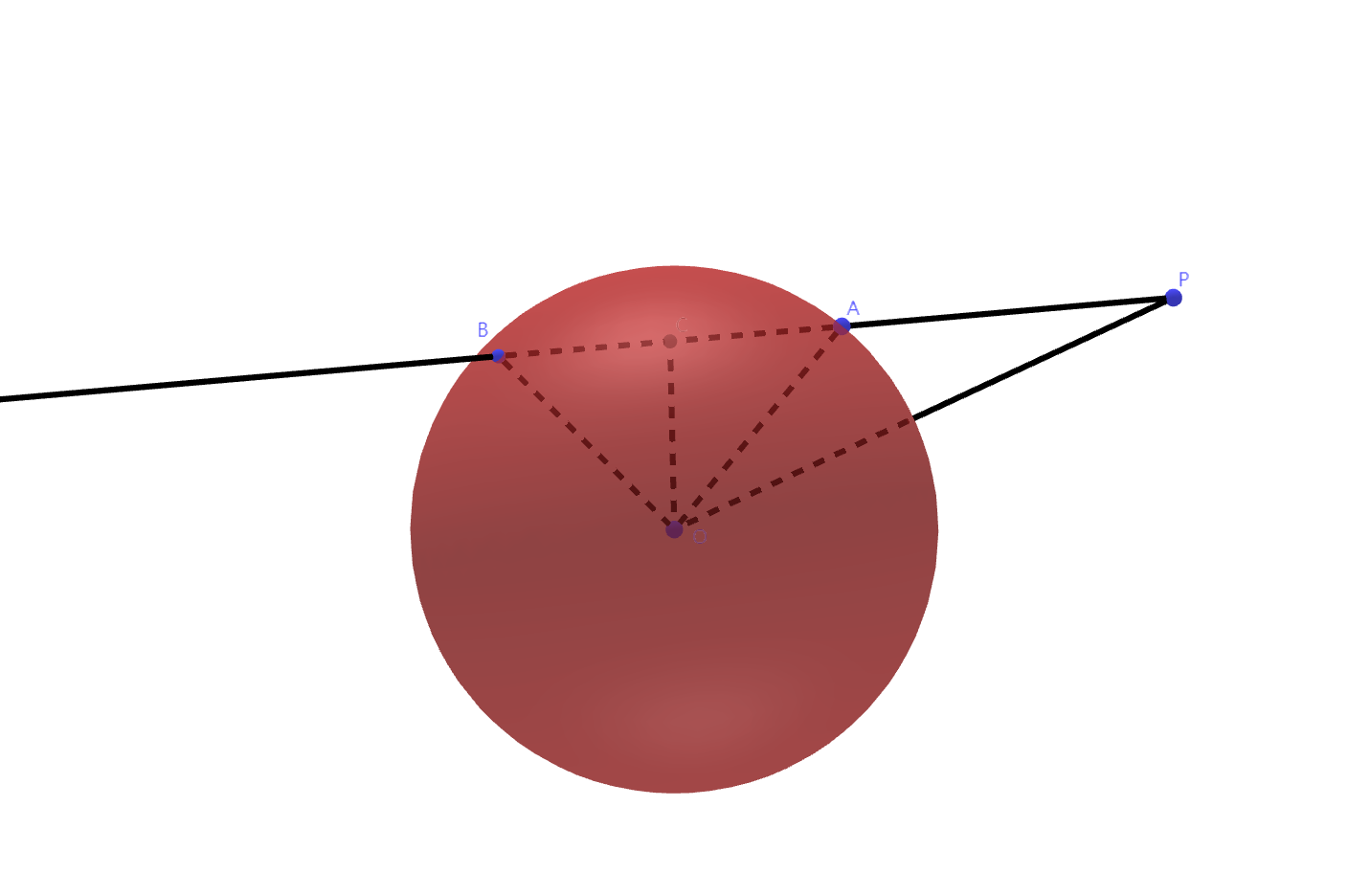
证明：
设$C$为$AB$中点，易得$OC \perp AB$。这样，

$$\begin{align} |PA| \cdot |PB| &= (|PC| - |AC|) (|PC| + |BC|) \\ &= |PC|^{2} - |AC|^{2} \\ &= (|OP|^{2} - |OC|^{2}) - (|OA|^{2} - |OC|^{2}) \\ &= |OP|^{2} - r^{2} \end{align}$$

相切时的情况证明类似。$\Box$

由球幂定理，就可以轻松推出球的相交弦定理、切割线定理和割线定理。

四面体

四个不共线的点两两相连，构成四个平面，这四个平面围成了一个四面体。四面体的六条棱可以分为三组对棱，每组对棱相互异面。

前面提到，四面体有一个唯一的外接球，这个外接球的球心就是四面体的外心（circumcenter）。将经过线段中点的垂面称为垂直平分面（perpendicular bisector），四面体的外心同时也是六条棱的垂直平分面的交点。

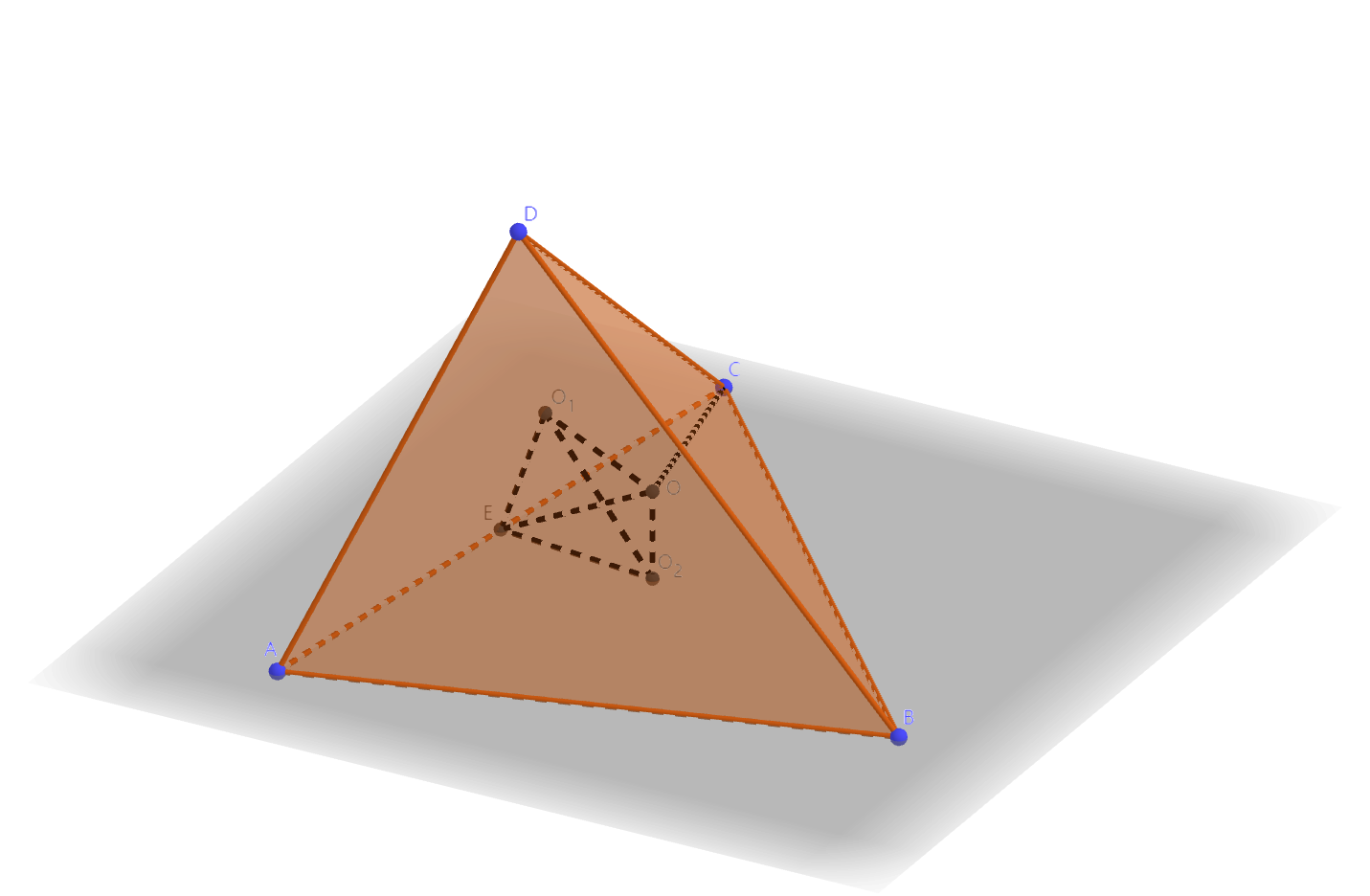
如图，设四面体$ABCD$的外心是$O$，三角形$ADC, ABC$的外心分别是$O_{1}, O_{2}$，$AC$中点是$E$，则$O, E, O_{1}, O_{2}$四点共圆。用平面几何可以求出$O_{1}E, O_{2}E$，根据二面角$D-AC-B$的值可以解三角形$O_{1}O_{2}E$，得到圆的直径$OE$。最后就能得到外接球半径

$$R = |OC| = \sqrt{|OE|^{2} + |CE|^{2}} = \sqrt{|OE|^{2} + \dfrac{1}{4} |AC|^{2}}$$

和三角形类似，四面体有外心，也自然有内心（incenter）。将经过二面角的棱，并且平分二面角的半平面称为角平分面（angle bisector），四面体的内心就是六个角平分面的交点。
和角平分线类似，角平分面上的点到二面角的两个半平面距离相等，其逆定理同样成立。转化为平面几何就能容易证明。
由这个定理可知，三面角的三个角平分面共线。

过四面体的内心可以作一个球与四面体的四个面都相切，因此四面体的内心同时也是四面体的内切球（inscribed sphere）的球心。总结成一个结论就是：
四面体的六个角平分面有唯一的交点，这个交点到四个面的距离相等。

这个结论的证明如下：
存在性：四面体$ABCD$中，$A$对应的三面角的三个角平分面共线$l$，$l$显然穿过$\triangle BCD$内部。二面角$A-BD-C$的角平分面经过线段$AC$，因此一定与$l$相交。设交点为$I$，则$I$到四面体的四个面距离相等。
唯一性：设点$I$到四面体的四个面距离相等，则$I$一定在六个二面角的角平分面上，也就是四个三面角对应直线的交点，这样的点至多只有一个。$\Box$

内心可以用于求四面体的体积。设四面体的内切球半径是$r$，四面体的表面积是$S$，则四面体的体积

$$V = \dfrac{1}{3} rS$$

用体积法可以证明：
设四面体$ABCD$的内心是$I$，则$V = V_{I-ABC} + V_{I-BCD} + V_{I-CDA} + V_{I-DAB}$。这四个三棱锥的高都是内切球半径$r$，因此$V = \dfrac{1}{3} r (S_{\triangle ABC} + S_{\triangle BCD} + S_{\triangle CDA} + S_{\triangle DAB}) = \dfrac{1}{3} rS$。$\Box$

类似可以得到角平分面的性质定理。设四面体$ABCD$中，二面角$D-AB-C$的角平分面与线段$DC$交于点$E$，则

$$\dfrac{|DE|}{|EC|} = \dfrac{S_{\triangle DAB}}{S_{\triangle ABC}}$$

将四面体的一个顶点与对面重心的连线称为四面体的中线（median），四面体的重心（centroid）就是四条中线的交点。
四面体的四条中线交于重心一点。设四面体$D-ABC$中，$DP$为一条中线，$G$为重心，则$\dfrac{|DG|}{|GP|} = 3$。

这个结论的证明如下：
如图，设四面体$D-ABC$中，$D_{1}, D_{2}, D_{3}$分别是$AB, BC, CA$的中点，则$\triangle ABC$的三条中线交于重心一点$P$，$DP$就是四面体的一条中线。设$Q$是$\triangle DBC$的重心，则$Q$在$DD_{2}$上，$AQ$也是四面体的一条中线。$DP, AQ \subset$平面$DAD_{2}$，所以两条中线显然相交，设交点是$G$。$G \in$平面$DBD_{3}$，则$CG$与平面$DAC$的交点在$DD_{3}$上，设交点是$R$。
在平面$DAD_{2}$中，过点$P$作$PE \parallel AQ$交$DD_{2}$于点$E$，则$\dfrac{|QE|}{|ED_{2}|} = \dfrac{|AP|}{|PD_{2}|} = 2$，得到$\dfrac{|DG|}{|GP|} = \dfrac{|DQ|}{|QE|} = 3$。
在平面$DBD_{3}$中，过点$G$作$GF \parallel BD_{3}$交$DD_{3}$于点$F$，则$\dfrac{|DF|}{|FD_{3}|} = \dfrac{|DG|}{|GP|} = 3, \dfrac{|FG|}{|D_{3}P|} = \dfrac{|AG|}{|AP|} = \dfrac{3}{4}$。那么$\dfrac{|RF|}{|RD_{3}|} = \dfrac{|FG|}{|D_{3}B|} = \dfrac{|FG|}{|D_{3}P|} \cdot \dfrac{|D_{3}P|}{|D_{3}B|} = \dfrac{1}{4}$，得到$\dfrac{|DR|}{|RD_{3}|} = 2$。因此$R$为$\triangle DAC$重心，$BR$是四面体的一条中线，三条中线交于一点。由于四面体的四个面相同，故四条中线交于一点。$\Box$

四面体的四条高并不一定交于一点，因此不是任何四面体都有垂心（orthocenter）。有垂心的四面体叫做垂心四面体（orthocentric tetrahedron）。
一个四面体是垂心四面体的充要条件是：三组对棱分别垂直。

证明：
充分性：如图，在四面体$ABCD$中，作$CE \perp AB$，垂足是$E$。因为$CD \perp AB$，所以$AB \perp$平面$CDE$，得到$DE \perp AB$。作$AF \perp BC$，垂足是$F$，同理可得$BC \perp$平面$ADF$，于是$DF \perp BC$。设$CE, AF$交于点$P$，则$P$为$\triangle ABC$的垂心。因为$DP \subset$平面$CDE$，所以$DP \perp AB$，同理$DP \perp BC$，得到$DP \perp$平面$ABC$，是四面体的一条高。同理，作$CG \perp BD$，垂足为$G$，$CG, DF$交于点$Q$，则$BD \perp$平面$ACG$，$AQ$也是四面体的一条高。此时$DP, AQ \subset$平面$ADF$，一定有交点，设交点为$H$。
因为$CH \subset$平面$CDE$，所以$CH \perp AB$；因为$CH \subset$平面$ACG$，所以$CH \perp BD$。这样得到$CH \perp$平面$ABD$，同理$BH \perp$平面$ACD$。因此四条高交于一点，$ABCD$就是垂心四面体。
必要性：因为$DP \perp$平面$ABC$，所以$CP$是$CD$在平面$ABC$的射影。$CP \perp AB$，由三垂线定理，$CD \perp AB$。同理，三组对棱分别垂直。$\Box$

还有进一步的定理：
若四面体的两组对棱分别垂直，则第三组对棱也垂直。

此外，从上面存在性的证明，可以得到垂心四面体的一个性质：
垂心四面体的任意一个顶点在对面的射影是对面三角形的垂心。

在棱长这一方面，垂心四面体有性质：
四面体$ABCD$是垂心四面体的充要条件是：

$$|AB|^{2} + |CD|^{2} = |AD|^{2} + |BC|^{2} = |AC|^{2} + |BD|^{2}$$