学习笔记·古典立体几何
立体几何基本公理
平面几何研究的对象是点（point）与直线（line），而在立体几何中，平面（plane）也成为了研究对象。
尽管平面是无限延伸的，但在画图时我们用一个平行四边形来表示平面。平面可以用一个希腊字母表示，例如\(\alpha,
\beta\)；也可以用平面内的点表示，例如平面\(ABCD\)。
平面几何是在欧几里得（Euclid，约前325—约前270）的五条公理上建立起来的，这些公理在立体几何中仍然成立，并与下面的三条立体几何基本公理共同构成了立体几何。
公理1：过不在同一直线上的三点有且只有一个平面。
这条公理也可以表述为“不共线的三点唯一确定一个平面”。
如果一个点\(A\)在平面\(\alpha\)内，那么记为\(A \in \alpha\)，否则记为\(A \notin \alpha\)。
公理2：若一条直线上的两个点都在平面内，则直线上的所有点都在该平面内。
如果一个点\(A\)在直线\(l\)上，那么记为\(A \in l\)，否则记为\(A \notin l\)。如果直线\(l\)上的所有点都在平面\(\alpha\)内，即直线\(l\)在平面\(\alpha\)内，那么记为\(l \subset \alpha\)，否则记为\(l \not\subset
\alpha\)。这样的记号实际上是把直线和平面看作点的集合。
公理2就能用形式化的语言表示为： \[A \in l, B
\in l, A \in \alpha, B \in \alpha \Rightarrow l \subset
\alpha\]
通过这两条公理，可以得到推论：
- 经过一条直线和直线外一点有且只有一个平面；
- 经过两条相交直线有且只有一个平面；
- 经过两条平行直线有且只有一个平面。
证明：
- 设直线\(l\)和点\(A\)。在直线\(l\)上取两点\(B, C\)，根据公理1，\(A, B, C\)三点确定唯一平面\(\alpha\)。因为\(B, C \in l\)，所以根据公理2，\(l \subset \alpha\)。\(\Box\)
- 设直线\(m, n\)相交于点\(A\)。在直线\(m\)上取点\(B\)，且\(A, B\)不重合；在直线\(n\)上取点\(C\)，且\(A, C\)不重合。根据公理1，\(A, B, C\)三点确定唯一平面\(\alpha\)。因为\(A, B \in m\)，所以根据公理2，\(m \subset \alpha\)，同理\(n \subset \alpha\)。\(\Box\)
- 设直线\(m \parallel n\)。在直线\(m\)上取两点\(A, B\)，在直线\(n\)上取点\(C\)。根据公理1，\(A, B, C\)三点确定唯一平面\(\alpha\)。因为\(A, B \in m\)，所以根据公理2，\(m \subset \alpha\)。在直线\(n\)上取除\(C\)外任意一点\(D\)，\(A, B, D\)三点确定平面\(\beta\)。因为\(C \in \alpha, m \parallel n\)，所以根据公理4，\(n \subset \alpha\)，所以\(D \in \alpha\)。因为\(A, B, D\)三点确定平面\(\beta\)，所以\(\alpha, \beta\)重合。\(\Box\)
两条直线不在同一平面内称为异面（skewness），异面直线没有公共点。两条直线有公共点称为相交（intersection），根据推论2，两条相交直线必然共面。无公共点且在同一平面内称为平行（parallelism）。
公理3：若两个不重合的平面有一个公共点，则它们有且只有一条过该点的公共直线，称为两个平面的交线（intersection
line）。
如图，平面\(\alpha,
\beta\)的交线是直线\(l\)，记为\(\alpha
\cap \beta = l\)。
公理3用形式化的语言可以表示为： \[P \in
\alpha, P \in \beta \Rightarrow \alpha \cap \beta = l, P \in
l\]
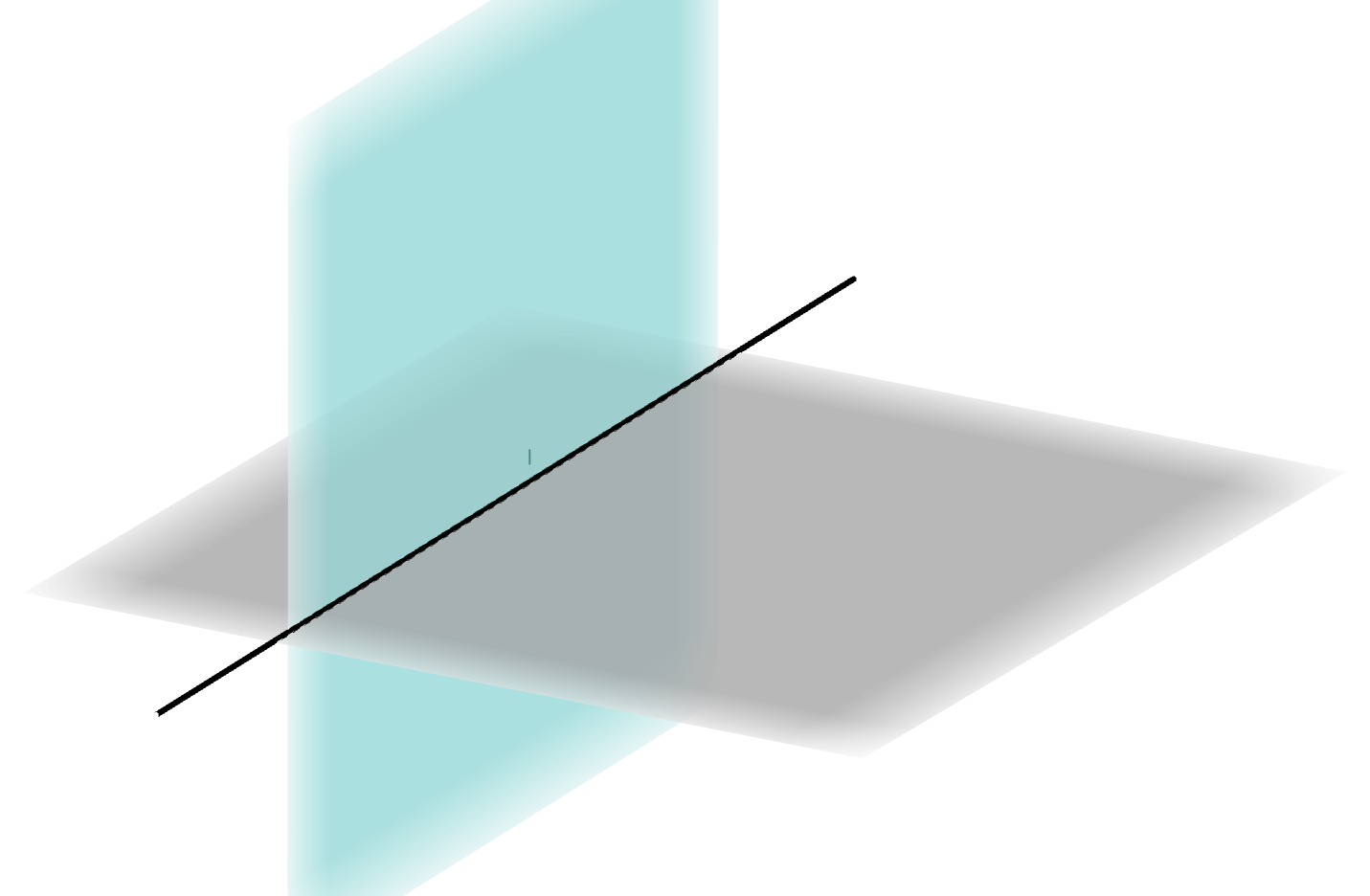
两个平面有交线称为相交（intersection），没有公共点称为平行（parallelism）。
对于直线和平面的位置关系：直线在平面内时，与平面有无数个公共点；直线与平面没有公共点称为平行（parallelism），既不在平面内又不与平面平行称为相交（intersection），这两者统称为在平面外。
相交的直线与平面有唯一的交点。
证明：
设直线\(l\)与平面\(\alpha\)相交。假设有两交点\(P, Q\)。\(P, Q
\in \alpha, P, Q \in l\)，由公理2，\(l
\subset \alpha\)，与相交的定义矛盾，故交点唯一。\(\Box\)。
此外，平面几何中的平行公理在立体几何中依然适用，这里一并列出。
公理4：过直线外一点，有且只有一条直线与该直线平行。
平行的判定与性质定理
直线与直线平行
由公理4，可以得到一个推论：
平行于同一直线的两条直线平行。
用形式化的语言表示就是： \[l \parallel m, l
\parallel n \Rightarrow m \parallel n\]
这条定理可以用于立体几何中直线与直线平行的判定。
证明这条定理需要用到后面的线面平行性质定理：
设\(l, m\)确定平面\(\alpha\)，\(l,
n\)确定平面\(\beta\)。不妨设\(\alpha, \beta\)不是同一个平面，则\(m \not\subset \beta\)。用反证法，假设\(m \nparallel n\)。
若\(m,
n\)共面，则一定相交，设交点为\(P\)。因为\(\alpha
\cap \beta = l, P \in m \subset \alpha, P \in n \subset
\beta\)，所以\(P \in \alpha \cap \beta
= l\)，\(l, m,
n\)三线共点，矛盾。
若\(m, n\)异面，因为\(m \parallel l, l \subset \beta, m \not\subset
\beta\)，所以\(\beta \parallel
\beta\)。任取点\(Q \in
n\)，\(m, Q\)确定一个平面\(\gamma\)。设\(\beta \cap \gamma = k\)，则\(Q \in k\)，且\(m
\parallel k\)。此时\(m \parallel
l\)，若\(l,
k\)相交，则情况同上，矛盾，因此\(l
\parallel k\)。由于\(m,
n\)异面，\(n,
k\)必不是同一条直线，则过一点\(Q\)可以作\(l\)的两条平行线\(n, k\)，与公理4矛盾。\(\Box\)
与此相关还有一个性质定理：
若两个角的边分别对应平行，则这两个角相等或互补。
证明：
如图，\(\angle ABC, \angle
DEF\)的两边对应平行，即\(AB \parallel
DE, BC \parallel EF\)。不妨设\(|AB| =
|DE|, |BC| = |EF|\)，\(AB,
DE\)方向相同。
首先证明\(EF,
BC\)方向相同时的情况。因为\(AB
\stackrel{\parallel}{=} DE\)，所以\(ABED\)是平行四边形，可得\(AD \stackrel{\parallel}{=}
BE\)。同理，\(CF
\stackrel{\parallel}{=} BE\)，所以\(AB
\stackrel{\parallel}{=} CF\)。因此，\(ACFD\)是平行四边形，\(|AC| = |DF|\)，故\(\triangle ABC \cong \triangle
DEF\)，从而\(\angle ABC = \angle
DEF\)。
对于\(EF,
BC\)方向相反时的情况，可以反向延长其中一条线，然后得到类似的结论。\(\Box\) 
直线与平面平行
对于直线与平面的平行关系，有判定定理：
若平面外一条直线与平面内的一条直线平行，则该直线与此平面平行。
用形式化的语言表示就是： \[l \not\subset
\alpha, m \subset \alpha, l \parallel m \Rightarrow l \parallel
\alpha\]
用反证法可以证明：
假设\(l \cap \alpha = P\)。直线\(l, m\)确定一个平面\(\beta\)，那么\(m
= \alpha \cap \beta\)。因为\(l \subset
\beta, m \subset \alpha\)，所以\(P \in
\alpha \cap \beta = m\)，得到\(l \cap m
= P\)，与平行矛盾。\(\Box\)
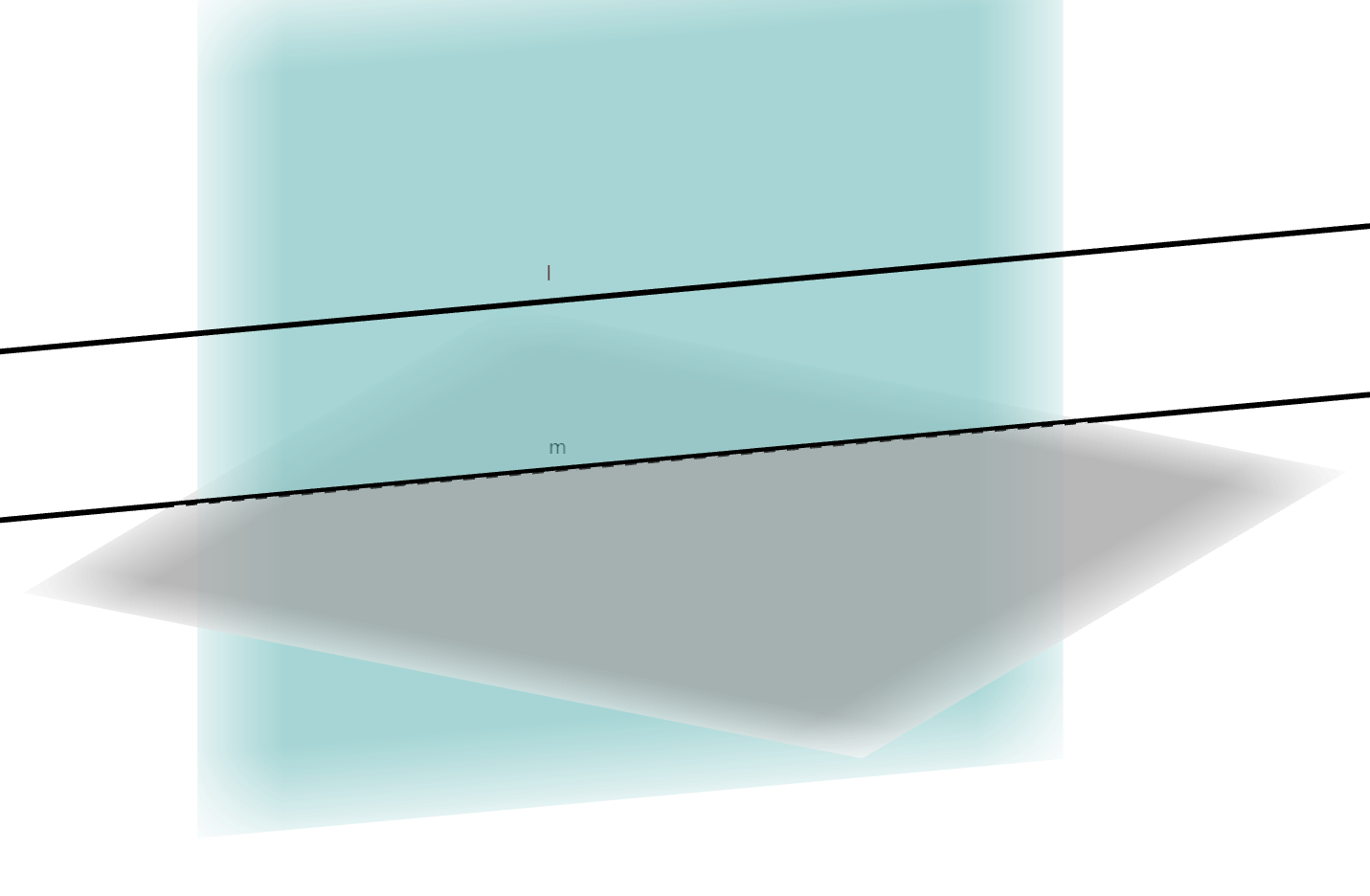
对于直线与平面的平行关系，有性质定理：
若一条直线与一个平面平行，且过该直线的平面与此平面相交，则该直线与交线平行。
用形式化的语言表示就是： \[l \parallel
\alpha, l \subset \beta, \alpha \cap \beta = m \Rightarrow l \parallel
m\]
证明：
因为\(l \parallel \alpha\)，所以\(l \cap \alpha = \varnothing\)，又\(m \subset \alpha\)，故\(l \cap m = \varnothing\)。\(l, m \subset \beta\)，由平行定义得到\(l \parallel m\)。
平面与平面平行
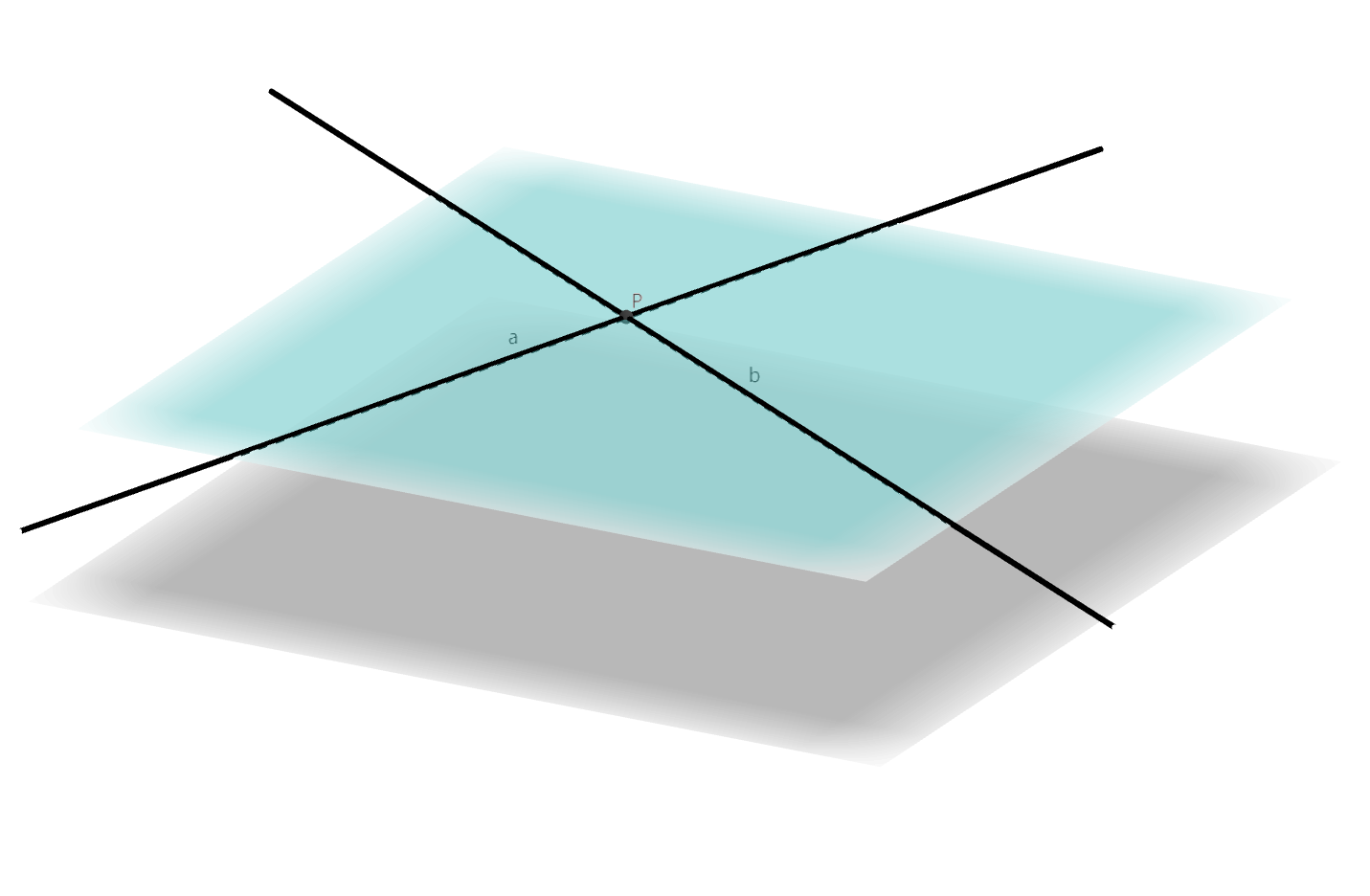
对于平面与平面的平行关系，有判定定理：
若一个平面内的两条相交直线都与另一个平面平行，则这两个平面平行。
用形式化的语言表示就是： \[a \subset \beta, b
\subset \beta, a \cap b = P, a \parallel \alpha, b \parallel \alpha
\Rightarrow \alpha \parallel \beta\]
用反证法可以证明：
假设\(\alpha \cap \beta =
l\)。不妨设\(a \cap l =
Q\)，则\(Q \in l = \alpha \cap
\beta\)，所以\(a \cap \alpha =
Q\)，与\(a \parallel
\alpha\)矛盾。若\(a \parallel l, b
\parallel l\)，则过一点\(P\)可以作\(l\)的两条平行线\(a, b\)，矛盾。\(\Box\)
由这个判定定理可以得到推论：
若两个平面内各有一组相交直线对应平行，则这两个平面平行。
对于平面与平面的平行关系，有两条性质定理：
两个平面平行，则其中一个平面上任意一条直线与另一个平面平行。
用形式化的语言表示就是： \[\alpha \parallel
\beta, l \subset \alpha \Rightarrow l \parallel \beta\]
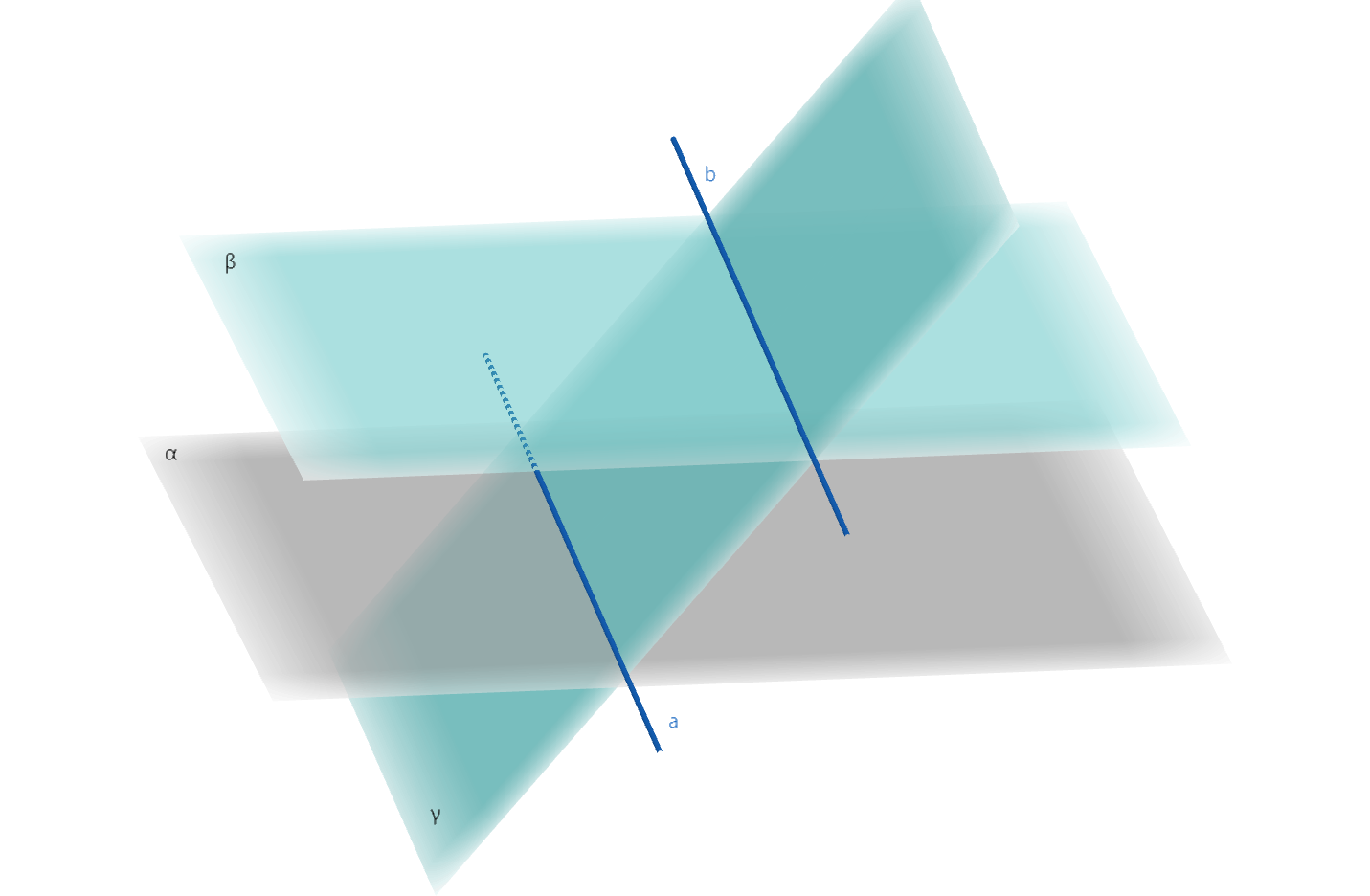
两个平面平行，若另一个平面与这两个平面相交，则两条交线平行。
用形式化的语言表示就是： \[\alpha \parallel
\beta, \gamma \cap \alpha = a, \gamma \cap \beta = b \Rightarrow a
\parallel b\]
证明：
因为\(\alpha \parallel
\beta\)，所以\(\alpha \cap \beta =
\varnothing\)，又\(a \subset \alpha, b
\subset \beta\)，故\(a \cap b =
\varnothing\)。\(a, b \subset
\gamma\)，由平行定义得到\(a \parallel
b\)。\(\Box\)
垂直的判定与性质定理
直线与直线垂直
在平面几何中，两条直线相交形成4个角，其中不大于\(\dfrac{\pi}{2}\)的称为两条直线的夹角。但在立体几何中，由于异面直线的存在，我们需要根据公理4，通过直线的平移来定义夹角。
设\(a, b\)是异面直线。在直线\(a\)上任取一点\(A\)，根据公理4，存在唯一的直线\(b'\)过点\(A\)且有\(b'
\parallel b\)。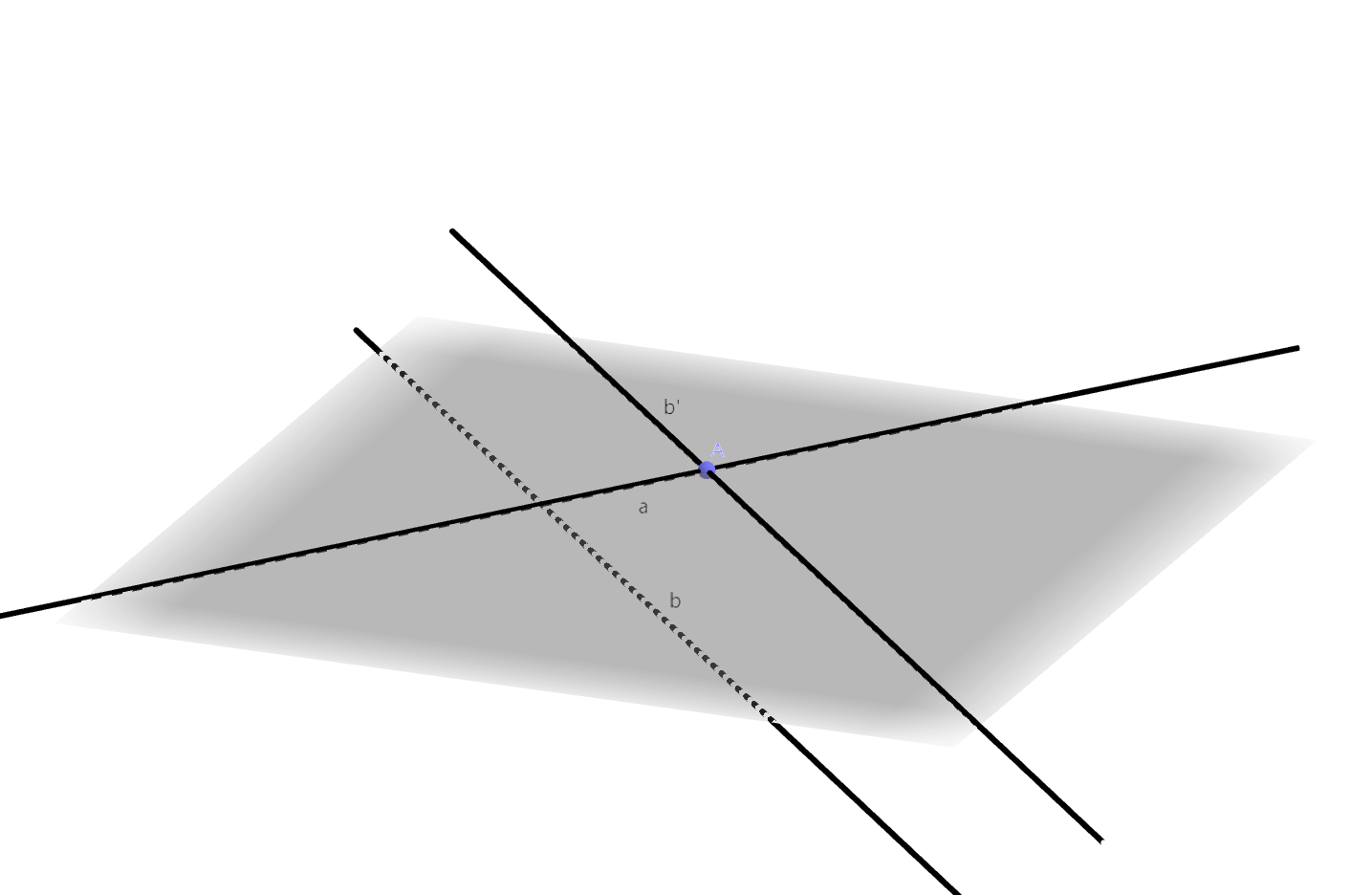 
异面直线\(a,
b\)的夹角（included angle）就是相交直线\(a, b'\)的夹角。夹角的范围是\([0, \dfrac{\pi}{2}]\)。
规定平行直线的夹角是\(0\)。
如果两条直线\(a, b\)的夹角是\(\dfrac{\pi}{2}\)，那么称两条直线垂直（perpendicularity），记作\(a \perp b\)。
直线与平面垂直
如果直线与平面内任意一条直线都垂直，那么称该直线与此平面垂直。直线\(l\)与平面\(\alpha\)垂直记作\(l \perp \alpha\)，若\(l \cap \alpha = P\)，则称\(P\)为垂足（foot）。
直线与平面垂直的判定同样只需要两条相交直线：
若一条直线与平面内的两条相交直线都垂直，则该直线与平面垂直。
用形式化的语言表示就是： \[l \perp a, l \perp
b, a \subset \alpha, b \subset \alpha, a \cap b = P \Rightarrow l \perp
\alpha\]
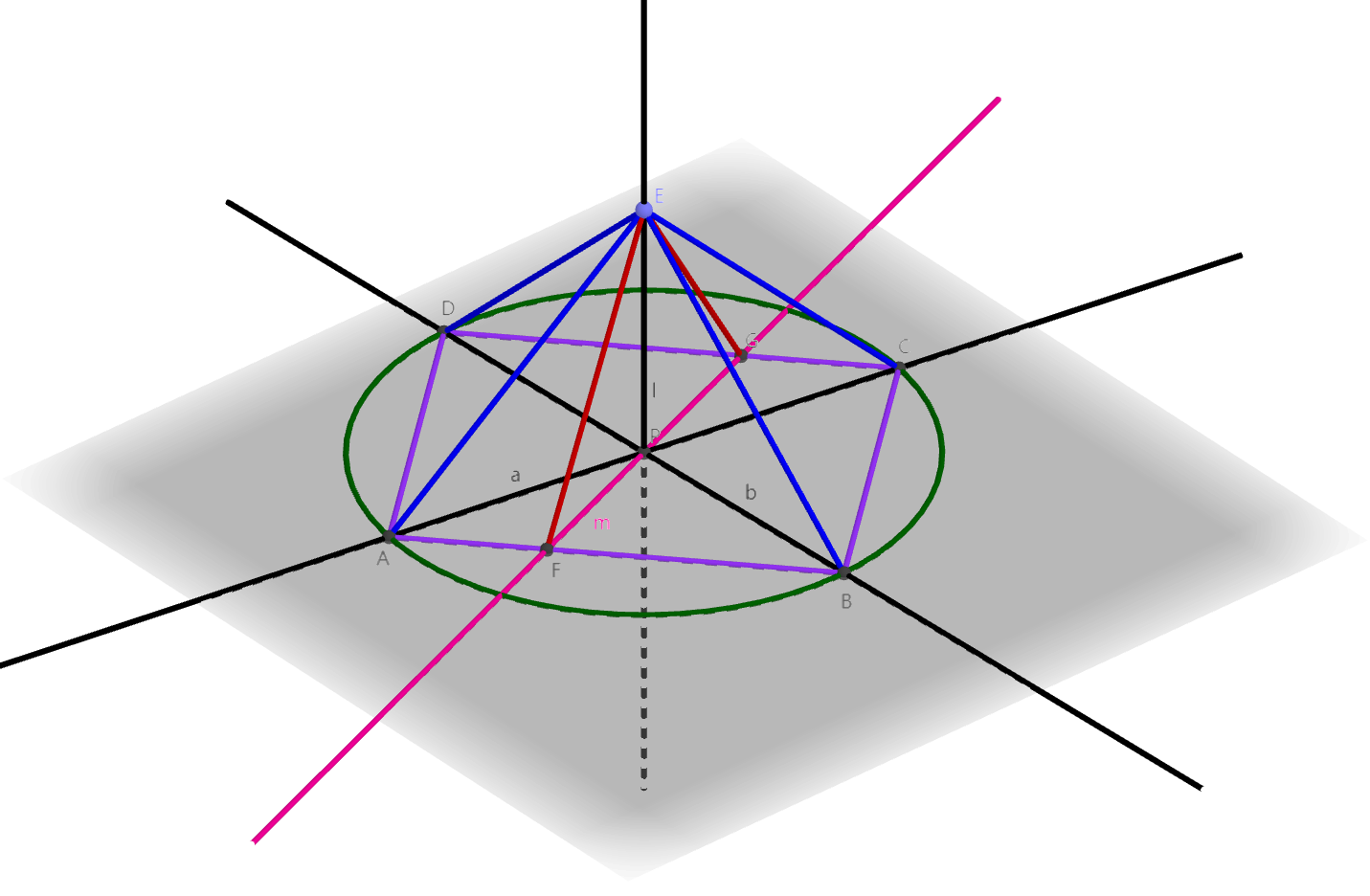可以把所有直线都平移到一起来证明：
如图，设\(l\)过点\(P\)，以\(P\)为圆心，任意长度为半径作一个圆，交\(a\)于点\(A,
C\)，交\(b\)于点\(B, D\)，任取\(E
\in l\)。此时\(|PA| = |PB| = |PC| =
|PD|\)，同时条件有\(\angle EPA = \angle
EPB = \angle EPV = \angle EPD = \dfrac{\pi}{2}\)，得到\(\triangle EPA \cong \triangle EPB \cong \triangle
EPC \cong \triangle EPD\)。这样有\(|EA|
= |EB| = |EC| = |ED|\)，并由圆的性质有\(|AB| = |CD|, |AD| = |BC|\)。
任取直线\(m \subset \alpha, P \in
m\)，\(m\)分别交\(AB, CD\)于点\(F,
G\)。\(ABCD\)是矩形，因此有\(AB \parallel CD\)，得到比例关系\(\dfrac{|AF|}{|GC|} = \dfrac{|FP|}{|PG|} =
\dfrac{|AP|}{|PC|} = 1\)，所以\(|AF| =
|CG|, |PF| = |PG|\)。容易得到，\(\triangle EAF \cong \triangle
ECG\)，从而\(|EF| =
|EG|\)。而\(|PF| =
|PG|\)，故\(\triangle EPF \cong
\triangle EPG\)，\(\angle EPF = \angle
EPG = \dfrac{\pi}{2}\)，因此\(l \perp
m\)。
由\(m\)的任意性，得\(l \perp \alpha\)。\(\Box\)
过平面外一点，有且只有一条直线与该平面垂直。
证明：
存在性：设\(O\)为平面\(\alpha\)外一点。任取\(m \subset \alpha\)，过点\(O\)作\(m\)的垂线，垂足为\(Q\)；过点\(Q\)在平面\(\alpha\)内作\(m\)的垂线\(n\)；过点\(O\)作\(n\)的垂线，垂足为\(P\)。因为\(OQ
\perp m, PQ \perp m\)，所以$m \(平面\)OPQ\(，得到\)m OP\(。而\)OP n\(，且\)m , n , m n = Q\(，所以\)OP \(。\
*唯一性*：假设\)OA, OB \(，则\)OA, OB\(相交于一点\)O\(。根据后面的线面垂直性质定理，\)OA OB\(，矛盾。\)$
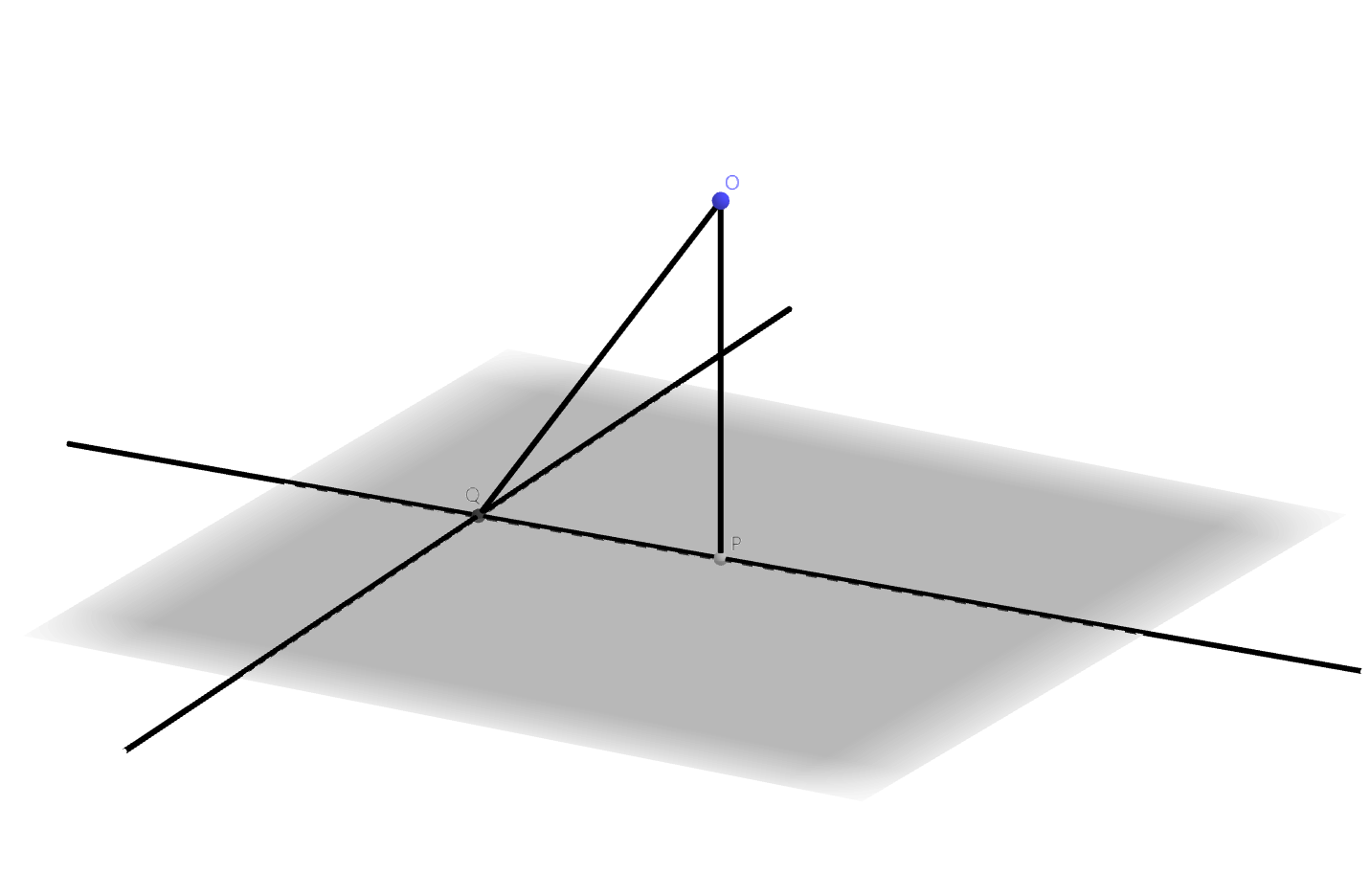
过点\(O\)作平面\(\alpha\)的唯一垂线，垂足为\(P\)，则线段\(OP\)称为点\(O\)到平面\(\alpha\)的垂线段（perpendicular
line segment），垂线段的长度\(|OP|\)称为点\(O\)到平面\(\alpha\)的距离（distance from a point to a
plane）。
\(OQ\)所在的直线与平面\(\alpha\)相交但不垂直，称为平面\(\alpha\)的斜线，交点\(Q\)称为斜足。\(\angle OQP\)称为直线\(OQ\)与平面\(\alpha\)所成的角。平面与其平行线所成的角是\(0\)，平面与其垂线所成的角是\(\dfrac{\pi}{2}\)，因此，直线与平面所成的角范围是\([0, \dfrac{\pi}{2}]\)。
直线\(PQ\)称为直线\(OQ\)在平面\(\alpha\)内的射影（projection）。
从上面存在性的证明得到启发，有三垂线定理：
平面内的直线与斜线垂直的充要条件是：该直线与斜线的射影垂直。
由三垂线定理可以得到三余弦定理：
平面内一条直线与该平面一条斜线夹角的余弦值，等于斜线与平面所成的角的余弦值，乘以平面内直线与斜线射影的夹角的余弦值。
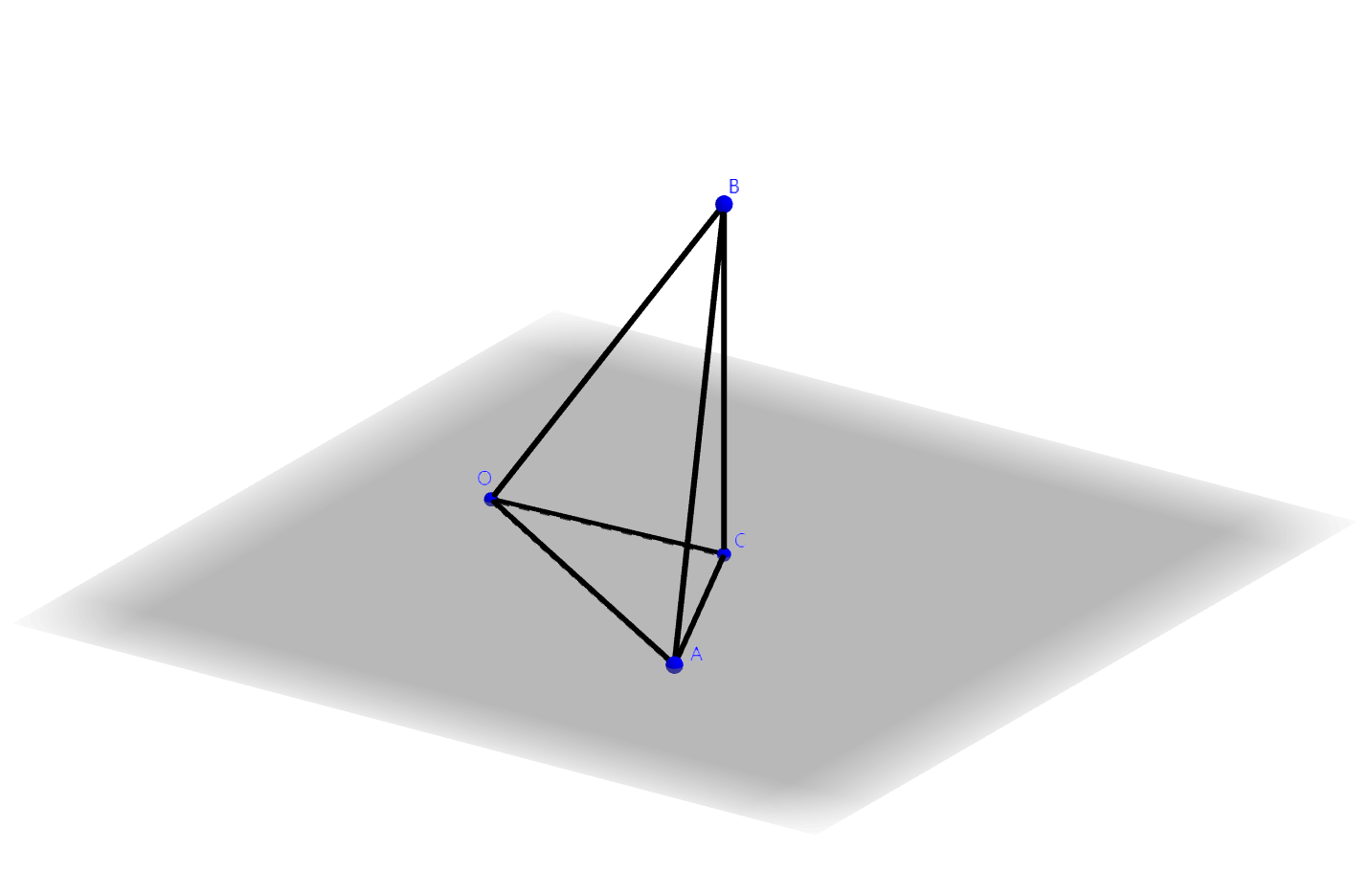如图，\(OA \subset \alpha\)，\(OC\)为斜线\(OB\)在平面\(\alpha\)的射影，三余弦定理有 \[\cos \angle AOB = \cos \angle AOC \cos \angle
BOC\]
下面是直线与平面垂直的性质：
垂直于同一平面的两条直线平行。
用形式化的语言表示就是： \[m \perp \alpha, n
\perp \alpha \Rightarrow m \parallel n\]
用反证法可以证明：
假设\(m \nparallel n\)。设\(n \cap \alpha = P\)，作直线\(m'\)过点\(P\)且有\(m'
\parallel m\)，则\(m' \cap n =
P\)。设\(m',
n\)确定平面\(\beta\)，\(\alpha \cap \beta = l\)。此时有\(m' \perp l, n \perp l\)，且\(m', n, l \subset \beta\)，得到\(m' \parallel n\)，矛盾。\(\Box\)
平面与平面垂直
一条直线把平面分成两部分，每一部分都叫做一个半平面（half-plane），直线叫做半平面的边界。一条直线与以它为边界的两个半平面组成了一个二面角（dihedral
angle）。这条直线叫做二面角的棱，两个半平面叫做二面角的面。棱为\(l\)，面分别为\(\alpha, \beta\)的二面角记作\(\alpha-l-\beta\)；也可在半平面\(\alpha, \beta\)内分别取点\(P, Q\)，棱用\(AB\)来表示，记作\(P-AB-Q\)。
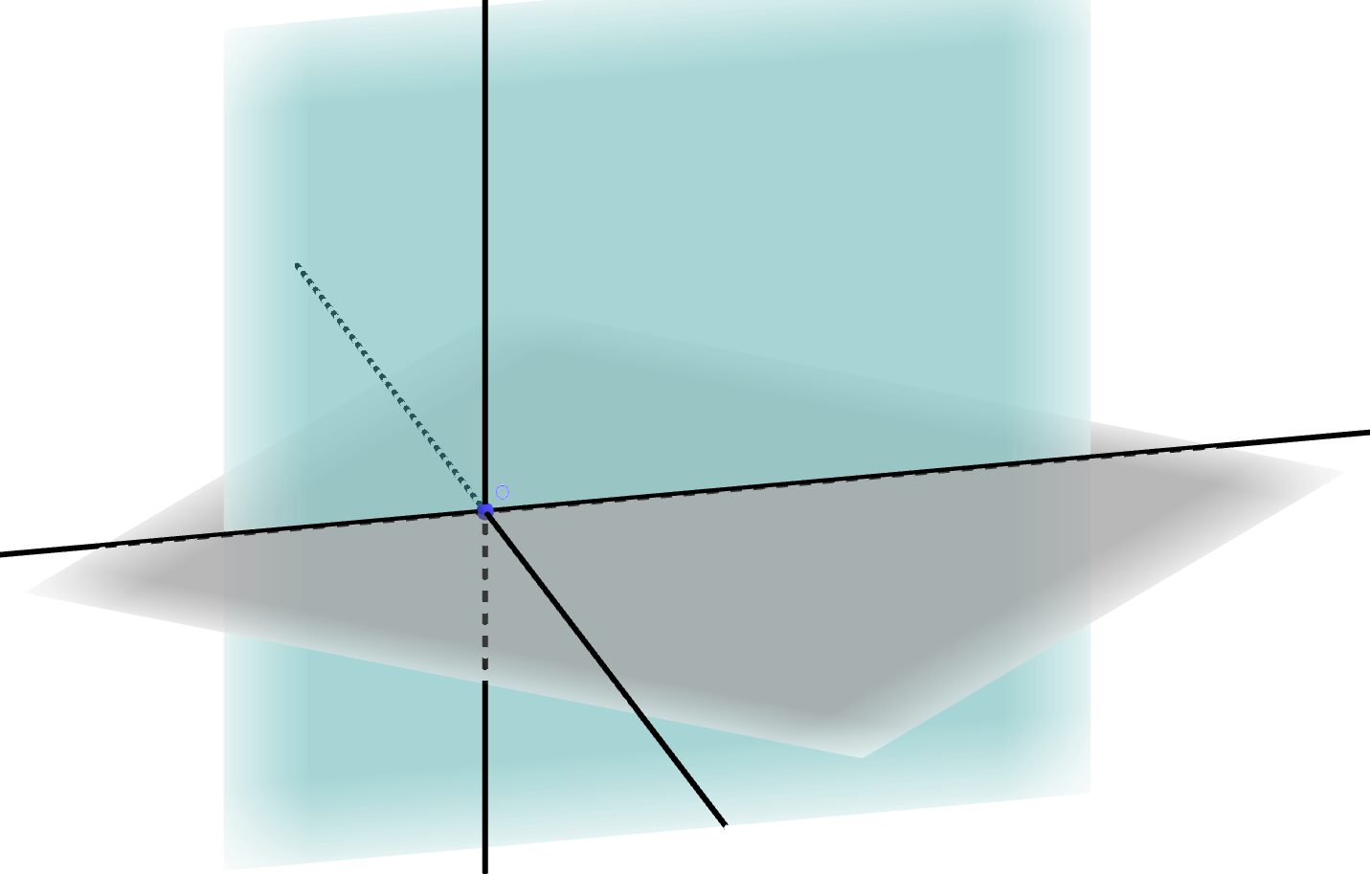
在二面角\(\alpha-l-\beta\)的棱\(l\)上任取一点\(O\)，在半平面\(\alpha, \beta\)内分别作射线\(OA \perp l, OB \perp l\)，则\(\angle
AOB\)称为二面角的平面角。二面角的大小就是其平面角的大小，取值范围是\([0, \pi]\)。
两个平行的平面所成的二面角大小规定为\(0\)。大小为\(\dfrac{\pi}{2}\)的二面角称为直二面角，此时两个平面垂直。平面\(\alpha, \beta\)垂直，记为\(\alpha \perp \beta\)。
解直角三角形可以得到三正弦定理：
设二面角\(\alpha-l-\beta\)的大小为\(x\)，半平面\(\alpha\)上一条直线与\(l\)的夹角为\(y\)，与平面\(\beta\)所成的角为\(z\)，则有 \[\sin
z = \sin x \sin y\]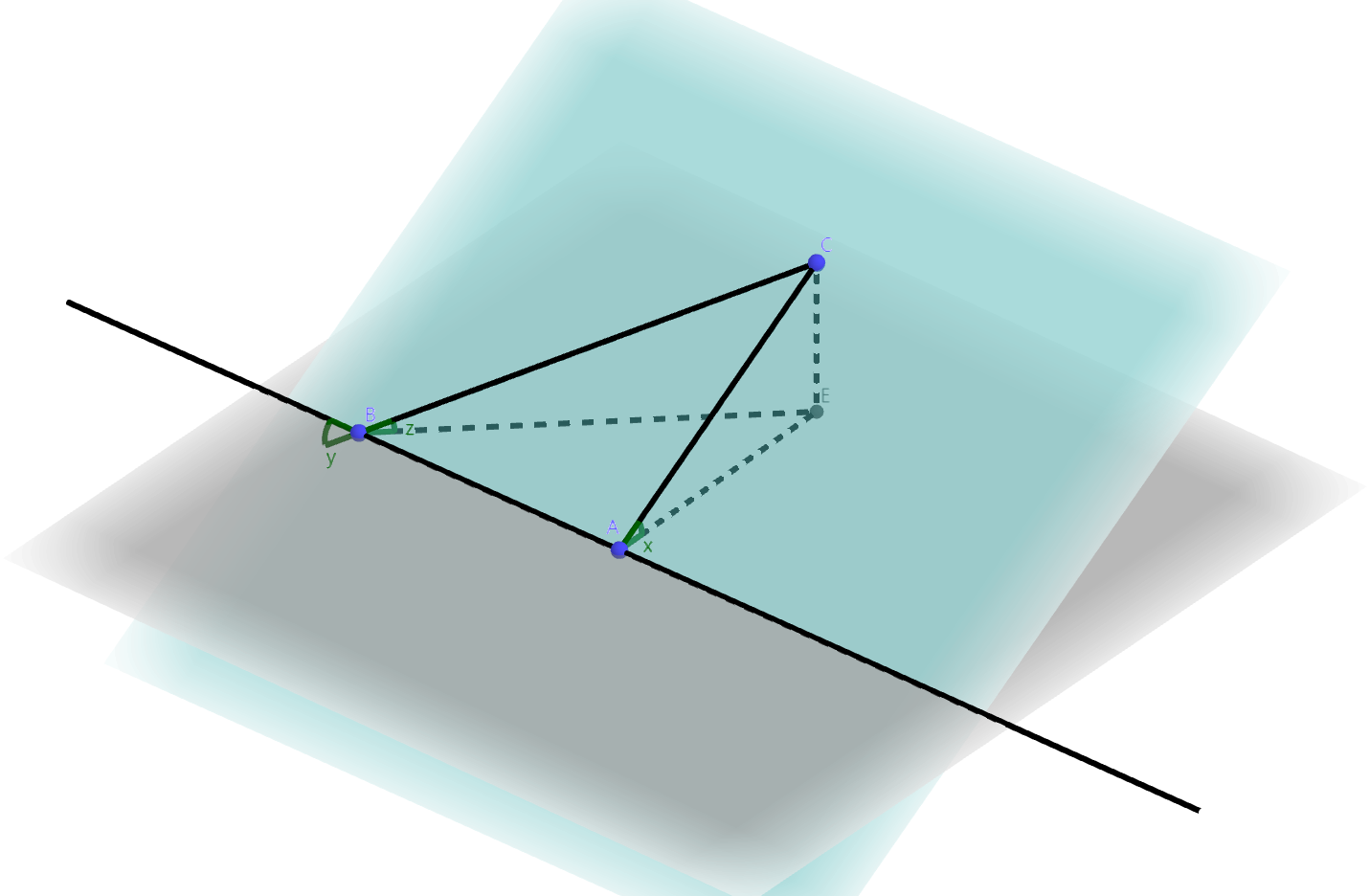 
对于平面与平面的垂直关系，有判定定理：
若一个平面过另一个平面的垂线，则这两个平面垂直。
用形式化的语言表示就是： \[l \perp \beta, l
\subset \alpha \Rightarrow \alpha \perp \beta\]
证明：
设\(\alpha \cap \beta = m\)，则\(m \subset \beta\)。由\(l \perp \beta\)，得到\(l \perp m\)。设\(l \perp m = O\)，过\(O\)在平面\(\beta\)内作\(m\)的垂线\(n\)。由\(l \perp
\beta\)，得到\(l \perp
n\)。此时\(l, n\)的夹角是\(\dfrac{\pi}{2}\)，即二面角\(\alpha-m-\beta\)的大小。\(\Box\)
对于平面与平面的垂直关系，有性质定理：
两个平面垂直，若一个平面内有一条直线垂直于这两个平面的交线，则这条直线垂直于另一个平面。
用形式化的语言表示就是： \[\alpha \perp
\beta, \alpha \cap \beta = l, a \subset \alpha, a \perp l \Rightarrow a
\perp \beta\]
证明：
设\(a \cap l = P\)，过点\(P\)在平面\(\beta\)内作\(l\)的垂线\(b\)。这样\(a,
b\)的夹角即二面角的大小\(\dfrac{\pi}{2}\)，\(a \perp b\)。而\(a \perp l, l \cap b = P, l \subset \beta, b
\subset \beta\)，故\(a \perp
\beta\)。\(\Box\)
几何体
基本几何体
多面体
多面体（polyhedron）是边界由若干个平面多边形组成的几何体。这些多边形叫做多面体的面（face），面的公共边叫做多面体的棱（edge），棱的公共点叫做多面体的顶点（vertex）。
有公共点的\(n (n \ge
3)\)条射线，以及相邻两条射线之间的平面，构成了一个多面角。这些射线叫做多面角的棱，公共点叫做多面角的顶点，平面叫做多面角的面。有\(n\)条棱的多面角称为\(n\)面角。相邻两条棱的夹角叫做多面角的平面角，相邻两个平面的夹角叫做多面角的二面角。
如果多面体的所有面都是全等的正多边形，并且所有多面角都全等，那么这样的多面体称为正多面体（regular
polyhedron）。正多面体只有5种：正四面体（regular
tetrahedron）、正六面体（正方体，cube）、正八面体（regular
octahedron）、正十二面体（regular
dodecahedron）、正二十面体（regular
icosahedron）。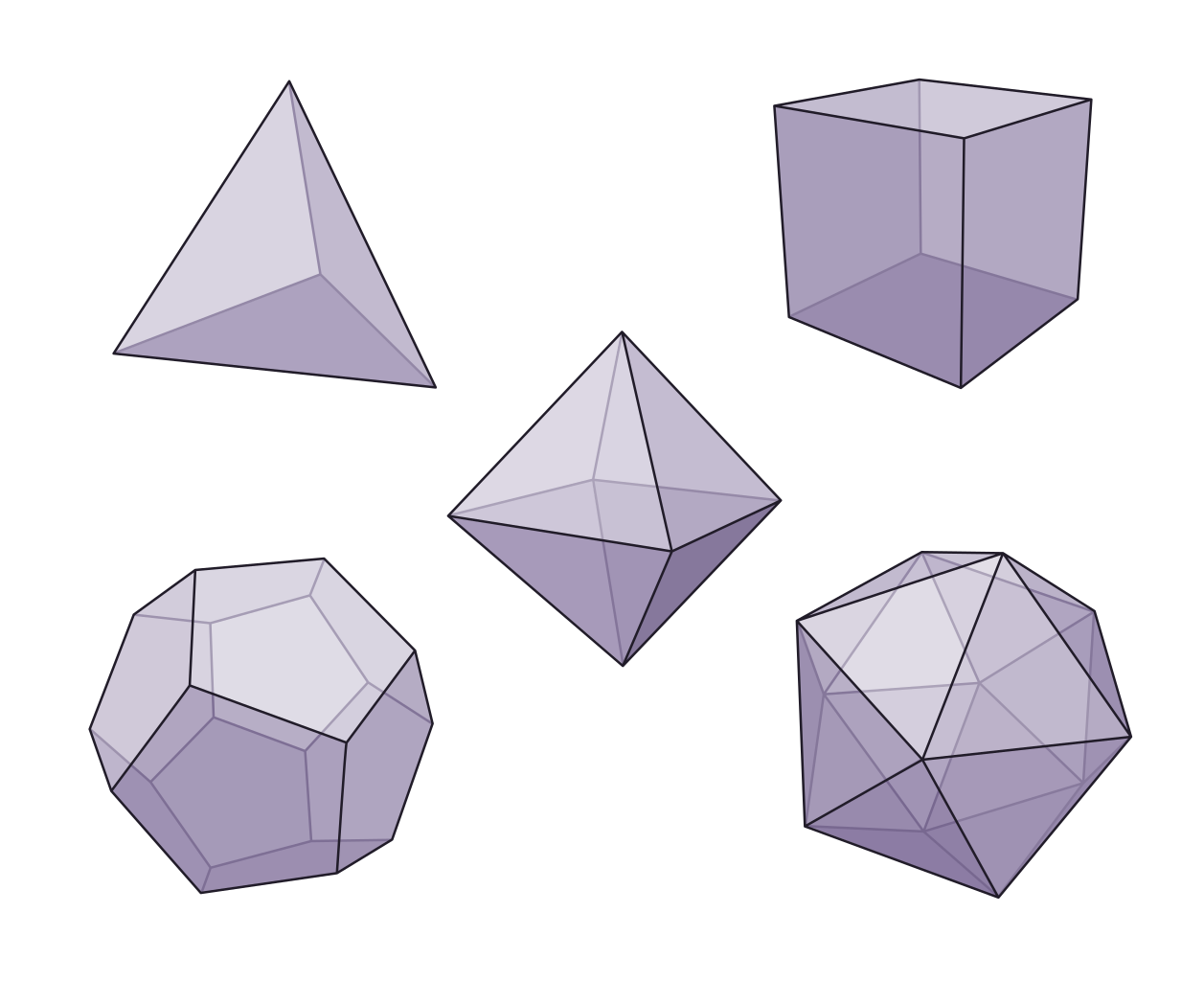 
棱柱（prism）是有两个面平行且全等，其余各面都是四边形，并且这些四边形的公共边都互相平行的多面体。两个平行的面叫做棱柱的底面（base），其余各面叫做棱柱的侧面，侧面的公共边叫做棱柱的侧棱。
侧棱垂直于底面的棱柱称为直棱柱（right
prism），否则称为斜棱柱（oblique
prism）。
底面为\(n\)边形的棱柱叫做\(n\)棱柱（n-gonal
prism），底面为正\(n\)边形的棱柱叫做正\(n\)棱柱（regular n-gonal
prism）。底面为平行四边形的棱柱又叫平行六面体（parallelepiped）。
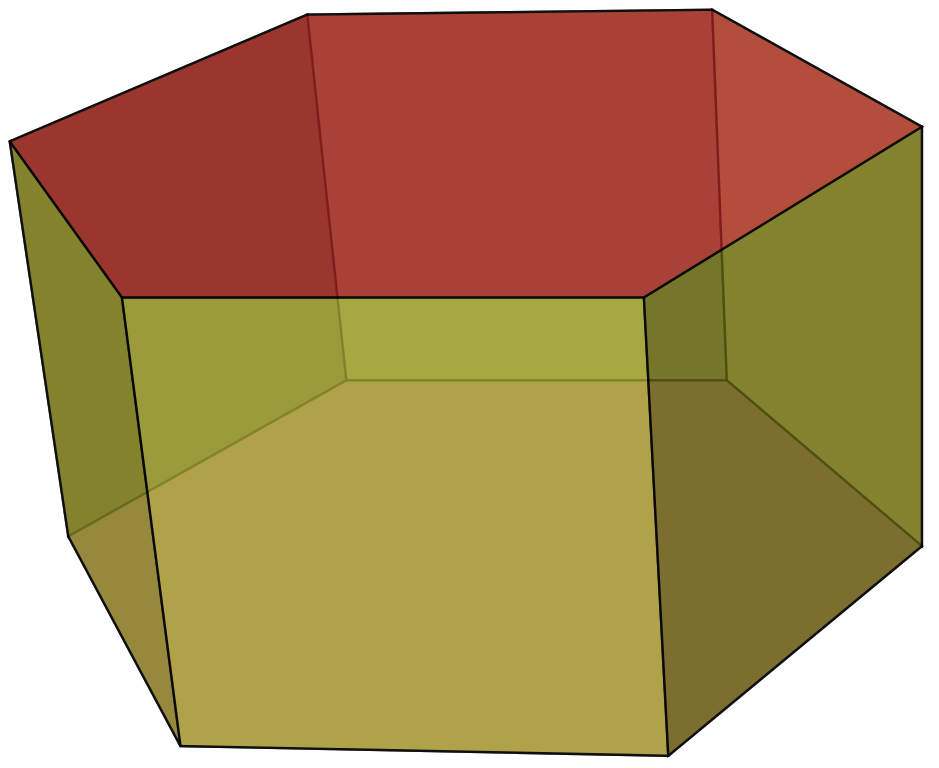
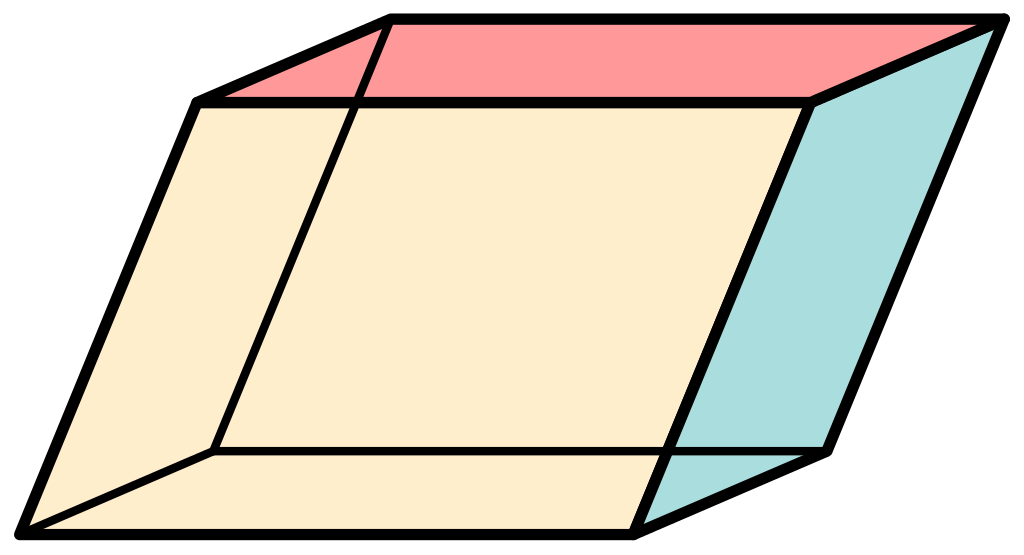棱柱用底面来表示。设棱柱的两个底面分别是\(n\)边形\(A_{1}
A_{2} \cdots A_{n}, B_{1} B_{2} \cdots B_{n}\)，其中\(A_{k},
B_{k}\)之间有侧棱连接，则棱柱表示为\(A_{1} A_{2} \cdots A_{n}-B_{1} B_{2} \cdots
B_{n}\)。
棱锥（pyramid）是多面角被一个平面所截得到的多面体。平面被多面角截得的面叫做棱锥的底面（base），其余各面叫做棱锥的侧面，侧面的公共边叫做棱锥的侧棱，多面角的顶点叫做棱锥的顶点（apex）。
底面为\(n\)边形的棱锥叫做\(n\)棱锥（n-gonal
pyramid），底面为正\(n\)边形且顶点与底面中心的连线垂直于底面的棱锥叫做正\(n\)棱锥（regular n-gonal
pyramid）。底面为三角形的棱锥又叫四面体（tetrahedron），所有棱长相等的四面体叫做正四面体。
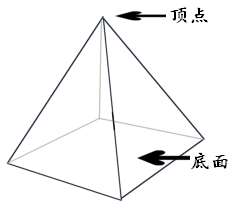棱锥用顶点和底面来表示。设棱锥的顶点是\(P\)，底面是\(n\)边形\(A_{1}
A_{2} \cdots A_{n}\)，则棱锥表示为\(P-A_{1} A_{2} \cdots
A_{n}\)。四面体的四个顶点都可以作为棱锥的顶点，所以设四个顶点是\(A, B, C, D\)，四面体也可以记为\(ABCD\)。
棱台（frustum）是用平行于棱锥底面的平面截棱锥，所得的底面与截面之间的部分。原棱锥的底面和截面分别叫做棱台的下底面和上底面，原棱锥的侧面截得的部分叫做棱台的侧面，原棱锥的侧棱截得的部分叫做棱台的侧棱。
底面和截面为\(n\)边形的棱台叫做\(n\)棱台（n-gonal frustum）。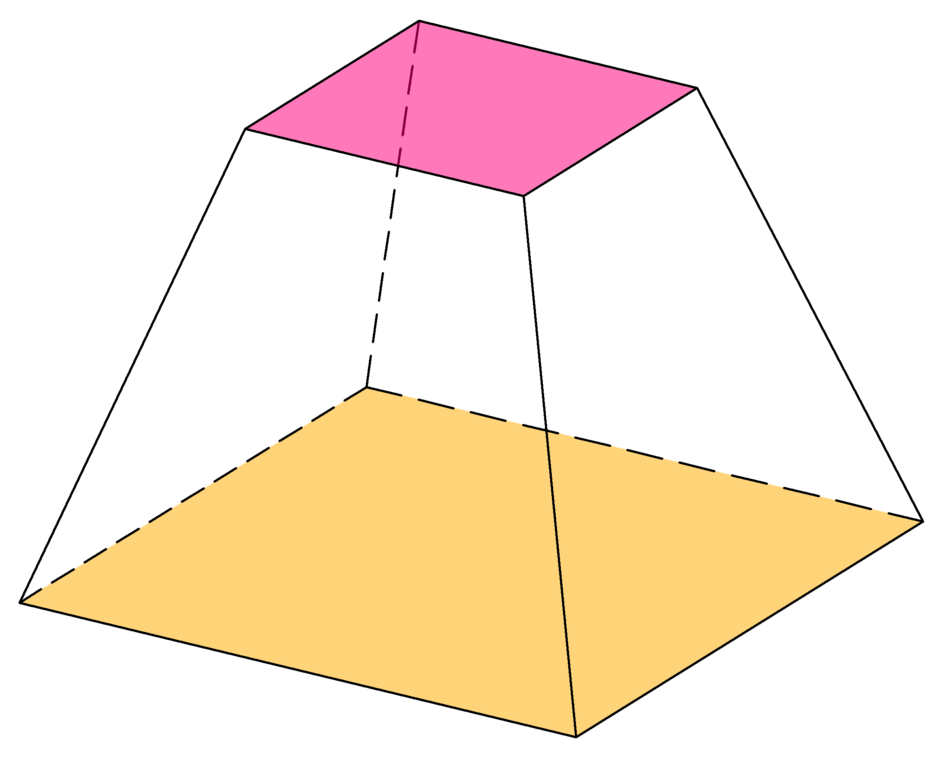 
棱台和棱柱一样，用底面来表示。
旋转体
旋转体（solid of revolution）是平面图形绕同一平面内的一条直线旋转一周形成的几何体。这条直线叫做旋转体的轴（axis）。
圆柱（cylinder）是矩形绕其一边旋转一周形成的旋转体。垂直于轴的边旋转而成的圆面叫做圆柱的底面，平行于轴的边旋转而成的曲面叫做圆柱的侧面，这条平行于轴的边旋转得到的任何线段都叫做圆柱的母线（generatrix）。
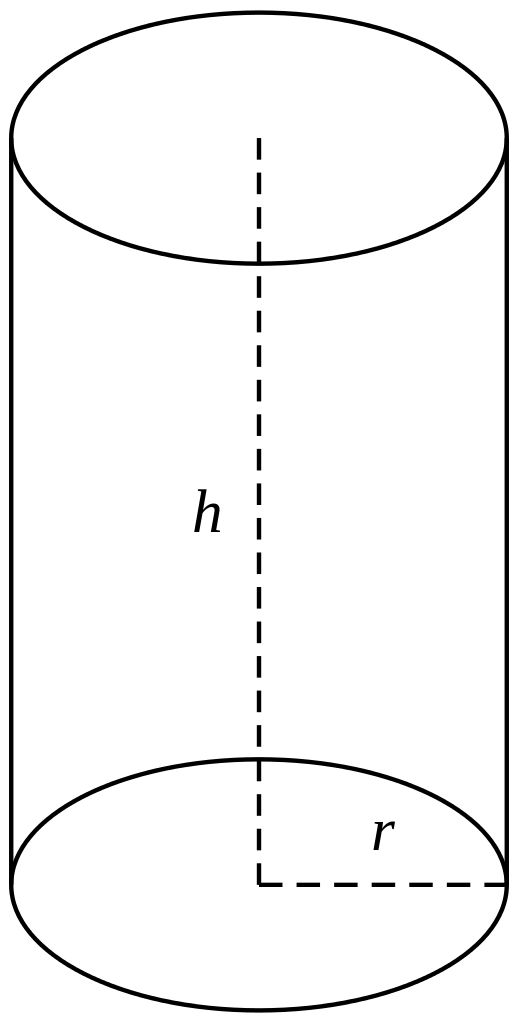圆柱用底面的圆心来表示。设圆柱底面的圆心是\(O_{1}, O_{2}\)，则圆柱表示为\(O_{1} O_{2}\)。
圆柱和棱柱都属于柱体。柱体是一个平面图形沿某一不在平面内的方向平移得到的几何体。如果这个方向与平面垂直，那么称为直柱体，否则称为斜柱体。两个底面之间的垂线段叫做柱体的高（height），圆柱的母线和高等长。
圆锥（cone）是直角三角形绕其一直角边旋转一周形成的旋转体。轴的非直角顶点叫做圆锥的顶点，另一条直角边旋转而成的圆面叫做圆锥的底面，斜边旋转而成的曲面叫做圆锥的侧面，斜边旋转得到的任何线段都叫做圆锥的母线。作为圆锥的轴的直角边叫做圆锥的高，圆锥的高与底面垂直。
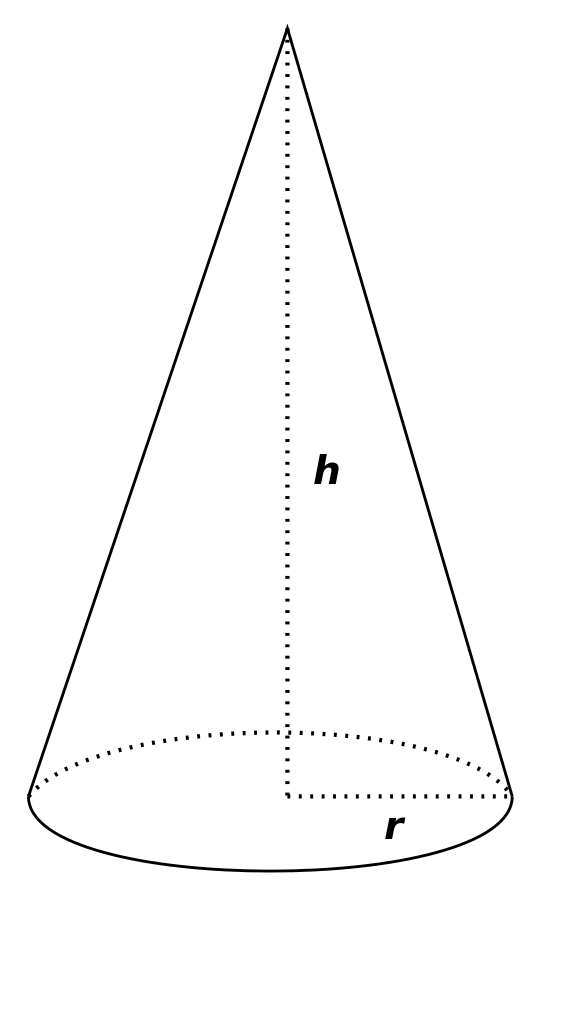圆锥用顶点和底面圆心来表示。设圆锥的顶点是\(S\)，底面的圆心是\(O\)，则圆锥表示为\(SO\)。
圆锥和棱锥都属于锥体。锥体是一个平面图形上的点与平面外一点所连线段的并集。过这一点的平面的垂线叫做锥体的高。
圆台（truncated
cone）是用平行于圆锥底面的平面截圆锥，所得的底面与截面之间的部分。原圆锥的底面和截面分别叫做圆台的下底面和上底面，原圆锥的侧面截得的部分叫做圆台的侧面，原圆锥的母线截得的部分叫做圆台的母线。
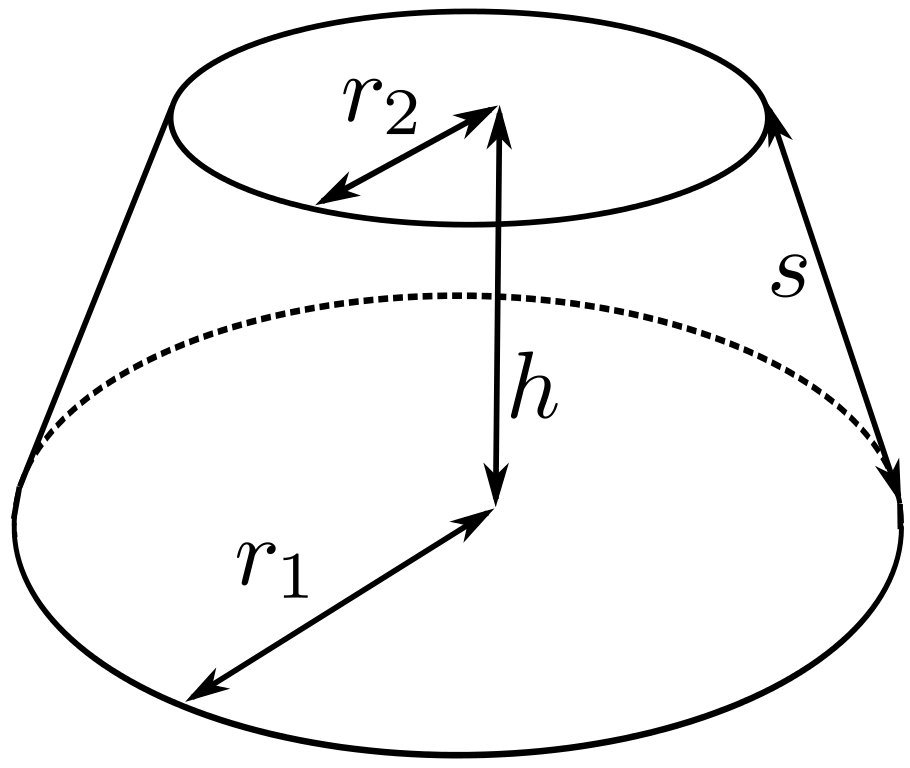圆台和圆柱一样，用底面的圆心来表示。
圆台的棱台都属于台体。台体是一个锥体被平行于锥体底面的平面所截，所得的底面与截面之间的部分。两个底面之间的垂线段叫做台体的高。
球（ball）是半圆绕其直径旋转一周形成的旋转体。半圆的圆心叫做球的球心（center），连接球心和球面上任意一点的线段叫做球的半径（radius）。
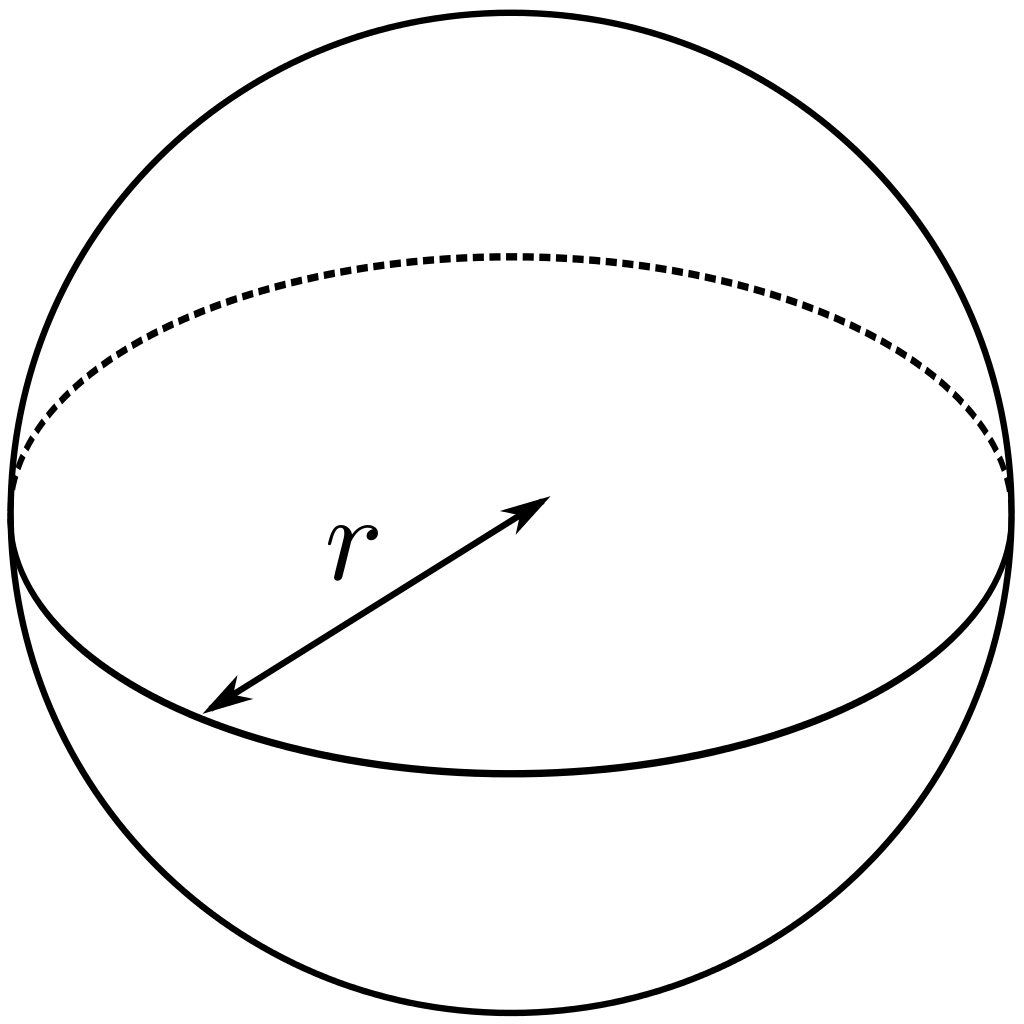球用球心表示。设球的球心是\(O\)，则球表示为\(O\)。
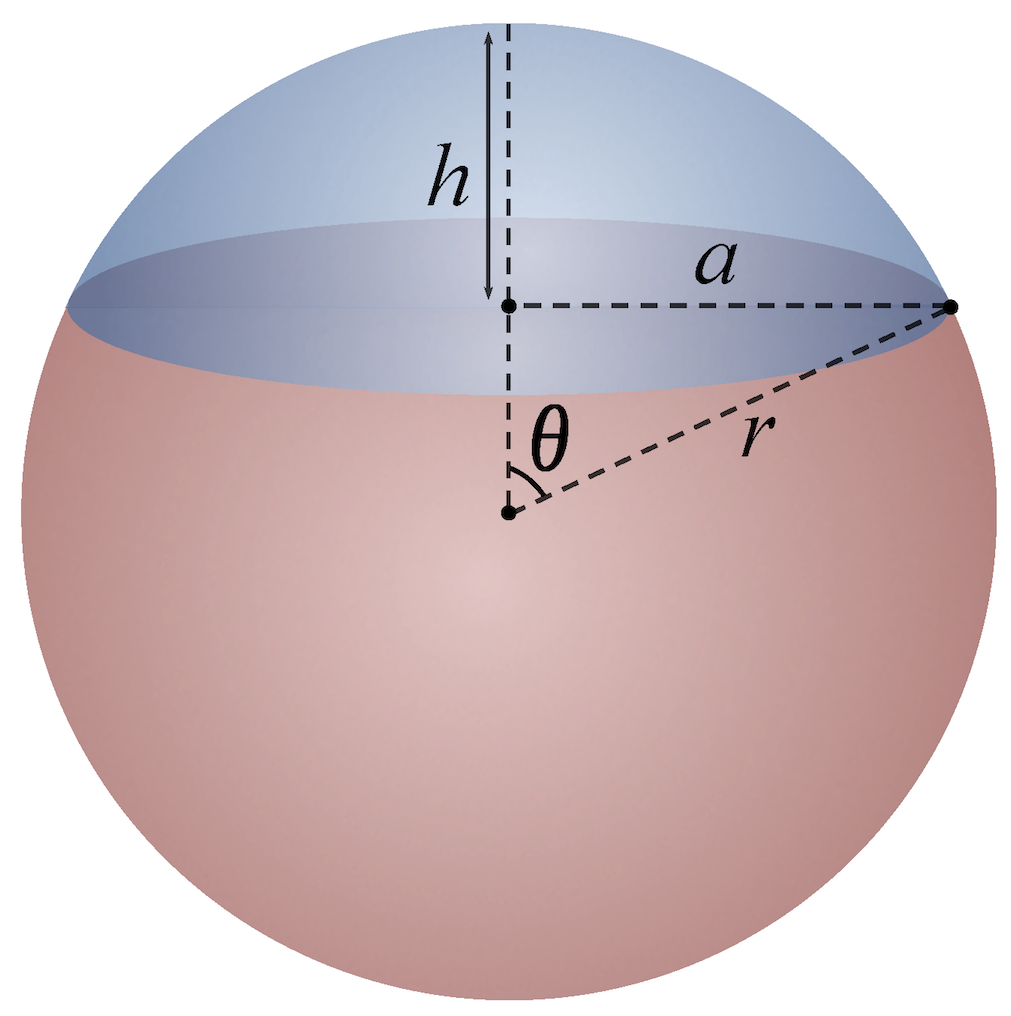
一个与球内部相交的平面把球分为两部分，每个部分都叫做球缺（spherical
cap）。截面叫做球缺的底面，球面与底面的最远距离叫做球缺的高。
几何体的表面积和体积
祖暅原理与体积公式
三国时期，魏国数学家刘徽（约225—约295）发现了《九章算术》中的一个错误：球的体积是同等高度和底面半径的圆柱体积的\(\dfrac{3}{4}\)。刘徽在一个正方体中内切两个垂直的圆柱，取这两个圆柱的交集，构造出一个几何体，他称为“牟合方盖”。刘徽发现，球的体积是对应的牟合方盖的\(\dfrac{3}{4}\)，而牟合方盖的体积又比圆柱小，因此《九章算术》给出的球的体积一定是错误的。只要能算出牟合方盖的体积，就能得到球的体积。
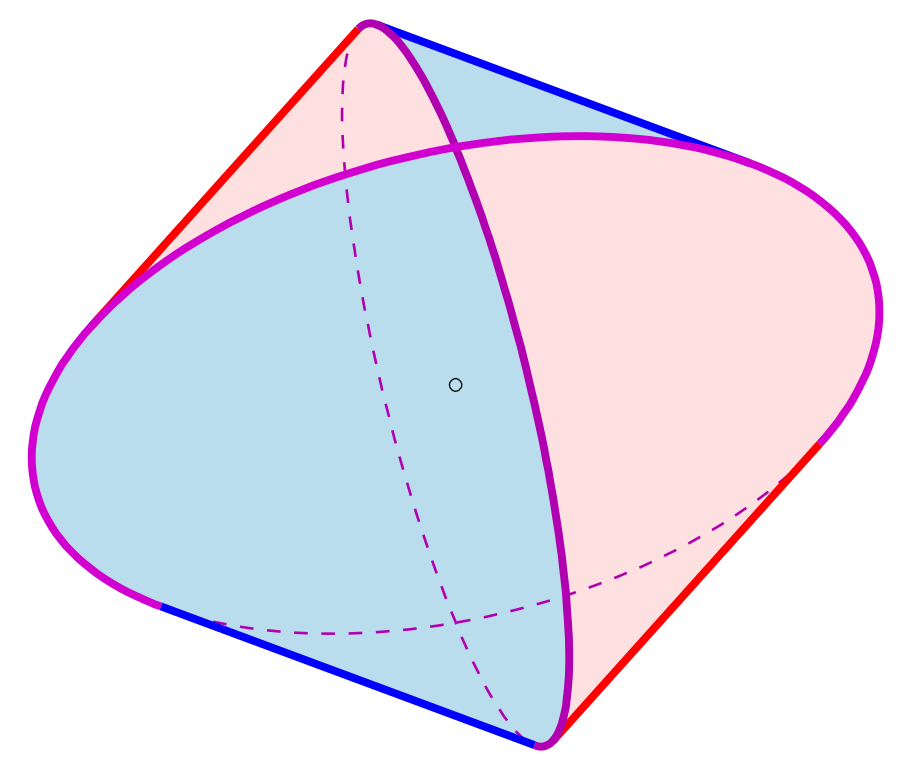不过，刘徽始终没能算出牟合方盖的体积。直到南北朝时期，祖冲之的儿子祖暅计算出了牟合方盖的体积，进而得到了导出各种几何体体积的通法，这就是祖暅原理：
幂势既同，则积不容异。
其含义是：
夹在两个平行平面之间的两个几何体，被平行于这两个平行平面的平面所截，若截得的两个截面积总是相等，则这两个几何体体积相等。
祖暅原理在17世纪由意大利数学家卡瓦列里（Bonaventura Cavalieri，1598—1647）重新发现，因此在西方被称为卡瓦列里原理（Cavalieri’s principle）。这个原理需要用到微积分才能解释。
首先，我们知道三条棱长为\(a, b, c\)的长方体体积公式为： \[V = abc\] 设柱体底面积为\(S\)，高为\(h\)，利用祖暅原理，作与柱体的底面积和高都相等的长方体，就能得到一般的柱体体积公式： \[V = Sh\]
由祖暅原理可得，所有底面积和高相等的锥体体积相等。那么，只要得到三棱锥的体积公式，就能作与锥体的底面积和高都相等的三棱锥，从而得到一般的锥体体积公式。
如图，已知三棱锥\(D-ABC\)，设其体积为\(V\)。过点\(D\)作平面\(\alpha\)平行于平面\(ABC\)，并分别过\(B, C\)作\(AD\)的平行线，交\(\alpha\)于点\(E,
F\)。这样得到三棱柱\(ABC-DEF\)。
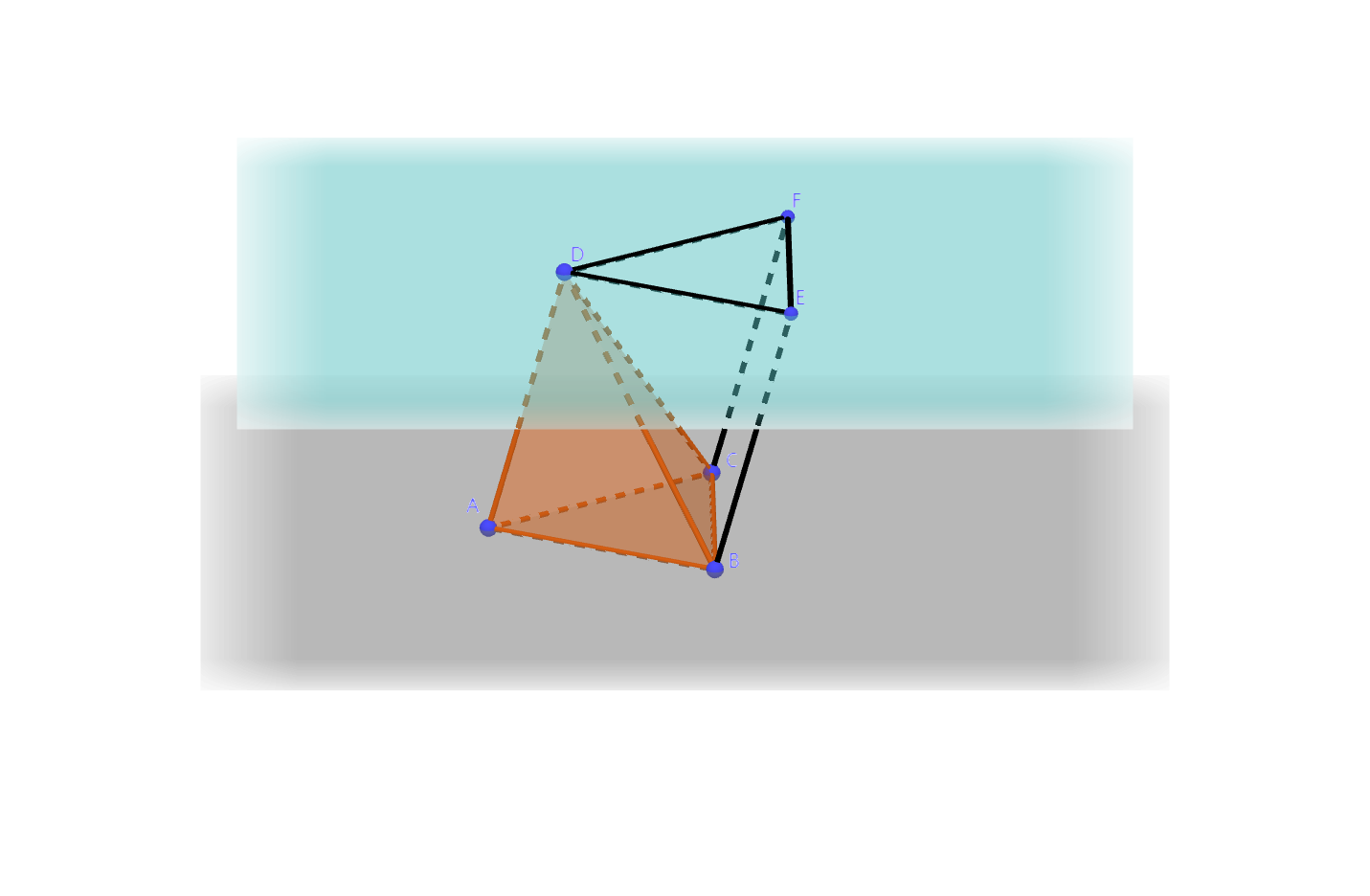三棱柱的体积是\(Sh\)，而三棱柱又由\(D-ABC, B-DEF,
B-CDF\)三个三棱锥组成，所以\(Sh = V +
V_{B-DEF} + V_{B-CDF}\)。因为\(\triangle ABC \cong \triangle
DEF\)，所以\(B-DEF,
D-ABC\)的底面积和高相等，\(V_{B-DEF} =
V\)；因为\(ACFD\)是平行四边形，所以\(\triangle CDF \cong \triangle
DCA\)，三棱锥\(D-ABC\)也可以写成\(B-DCA\)，\(B-CDF,
B-DCA\)的底面积和高相等，\(V_{B-CDF} =
V\)。代入得\(Sh =
3V\)，这样就得到锥体体积公式： \[V = \dfrac{1}{3} Sh\]
台体的体积可以通过转化为锥体来解决。设台体的两个底面积为\(S, S'\)，高为\(h\)。如图，已知三棱台\(ABC-DEF\)，不妨设\(S' < S\)，沿\(S'\)方向延长侧棱，交于一点\(G\)，得到三棱锥\(G-ABC\)。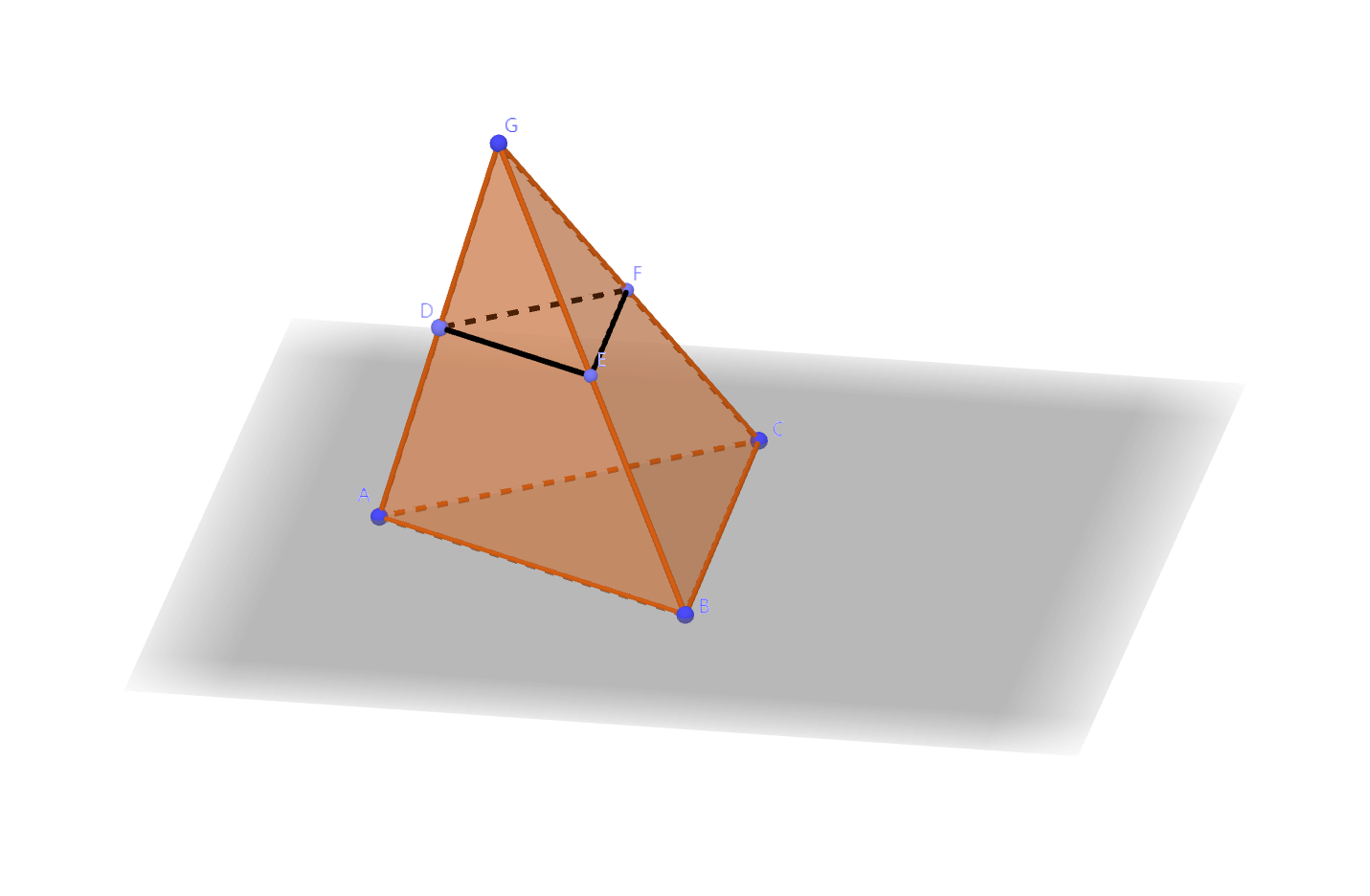 
两个底面图形相似，上下底面相似比为\(k =
\sqrt{\dfrac{S'}{S}}\)。设点\(G\)到上、下底面的距离分别是\(h_{1}, h_{2}\)，则\(h_{1} = kh_{2}, h = h_{2} -
h_{1}\)，从而得到\(h_{2} = \dfrac{1}{1
- k} h, h_{1} = \dfrac{k}{1 - k} h\)。
根据锥体体积公式， \[
\begin{align}
V &= \dfrac{1}{3} (Sh_{2} - S'h_{1}) \\
&= \dfrac{1}{3 (1 - k)} (S - kS') h \\
&= \dfrac{1}{3} (\dfrac{\sqrt{S^{3}} - \sqrt{S'^{3}}}{\sqrt{S} -
\sqrt{S'}}) h \\
&= \dfrac{1}{3} (S + \sqrt{SS'} + S') h
\end{align}
\] 于是，台体体积公式： \[V = \dfrac{1}{3} (S + \sqrt{SS'} + S')
h\]
特别地，圆柱、圆锥、圆台体积公式分别为： \[ \begin{align} & V = \pi r^{2} h \\ & V = \dfrac{1}{3} \pi r^{2} h \\ & V = \dfrac{1}{3} \pi (r_{1}^{2} + r_{1} r_{2} + r_{2}^{2}) h \end{align} \] 其中，\(r\)是圆柱、圆锥的底面半径，\(r_{1}, r_{2}\)是圆台的两个底面的半径。
圆柱、圆锥、圆台的表面积公式
圆柱、圆锥、圆台的底面都是圆，所以问题主要是侧面积的计算。我们可以通过展开图（net）来计算侧面的面积。
圆柱侧面的展开图是一个矩形，一条边长是底面的周长\(2 \pi r\)，另一条边长是圆柱的高\(h\)，因此加上两个底面的圆，就得到圆柱表面积公式：
\[S = 2 \pi r (r + h)\]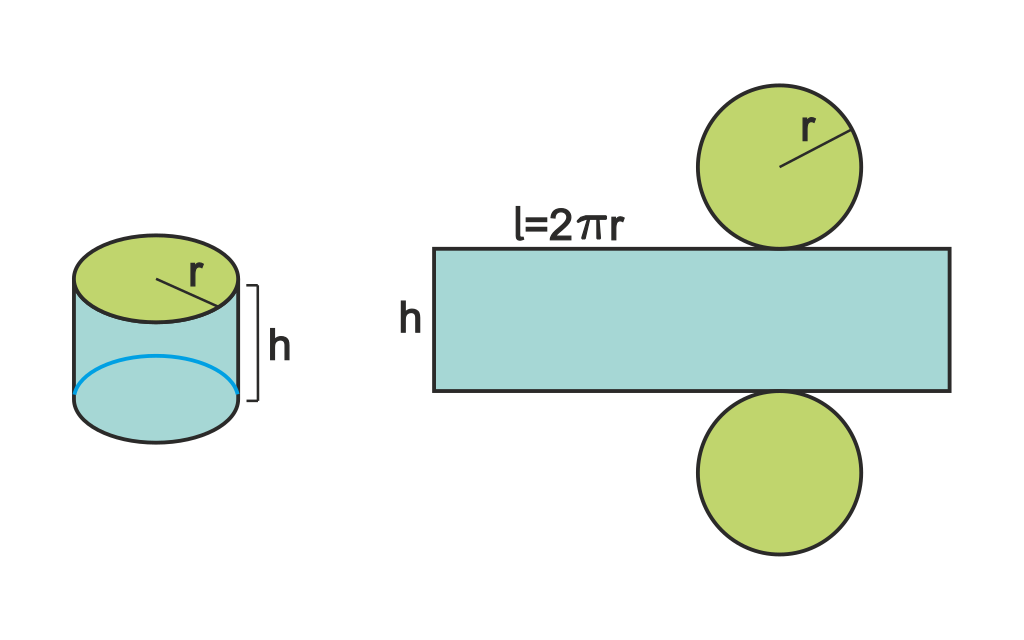 
圆锥侧面的展开图是一个扇形，半径是母线长\(l\)，弧长是底面的周长\(2 \pi
r\)，所以圆锥表面积公式是： \[S = \pi r (r + l)\] 
圆台侧面的展开图是一个扇环，内外半径差是母线长\(l\)，内、外弧长分别是两个底面的周长\(2 \pi r_{1}, 2 \pi
r_{2}\)，所以圆台表面积公式是： \[S = \pi (r_{1}^{2} + r_{2}^{2} + r_{1} l + r_{2}
l)\]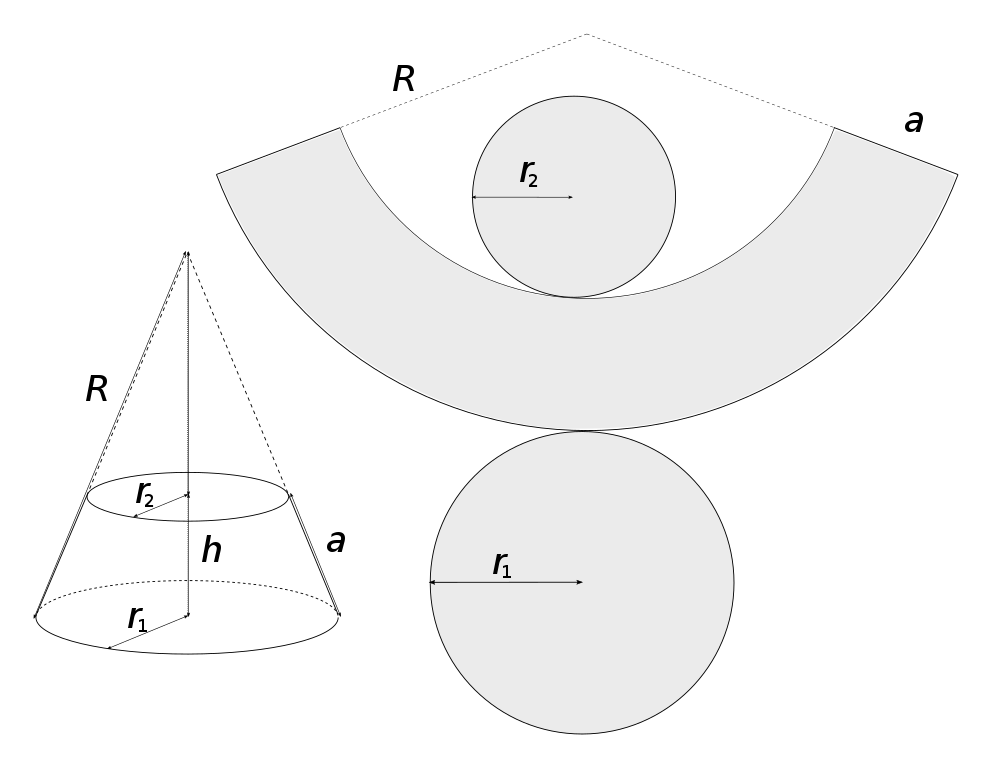 
球的表面积和体积公式
前面提到，刘徽用牟合方盖给出了计算球的体积的方法。而在刘徽之前，古希腊数学家阿基米德（Archimedes，约前287—约前212）用另一种方法算出了球的体积： \[V = \dfrac{4}{3} \pi r^{3}\] 其中\(r\)是球的半径。
接下来用阿基米德的方法来证明：
设球的体积为\(V\)，半径为\(r\)。如图，构造一个底面半径和高都等于\(r\)的圆柱，并挖去一个圆锥。平面\(\alpha\)经过球的球心和圆柱的底面与圆锥的顶点。
首先，平面\(\alpha\)上面的半球和圆柱的底面积相等。然后任意作一个与平面\(\alpha\)平行的平面\(\beta\)截半球和右边的几何体，设\(\alpha\)与\(\beta\)的距离为\(d\)。截面和半球相交得到一个圆，半径为\(\sqrt{r^{2} - d^{2}}\)，所以面积为\(\pi (r^{2} -
d^{2})\)；右边的几何体截面是一个圆环，内半径由相似关系得到是\(d\)，外半径是\(r\)，所以圆环面积为\(\pi (r^{2} -
d^{2})\)。这样，两者截面积总是相等，根据祖暅原理，半球和右边的几何体体积相等。而这个几何体的体积可以直接计算：
\[\dfrac{1}{2} V = \pi r^{2} \cdot r -
\dfrac{1}{3} \pi r^{2} \cdot r = \dfrac{2}{3} \pi r^{3}\]
于是得到球的体积\(V = \dfrac{4}{3} \pi
r^{3}\)。\(\Box\)
球的表面积公式是： \[S = 4 \pi r^{2}\]
可以通过细分球面的方法来证明：
如图，把球面按照经纬线的方式分成很多小块，设有\(n\)块，每块面积为\(S_{i}\)，则\(\sum\limits_{i=1}^{n} S_{i} = S\)。 
如果每块足够小，那就可以近似地看为锥体，所以\(V_{i} \approx \dfrac{1}{3} r S_{i}\)，从而
\[V \approx \sum\limits_{i=1}^{n} V_{i} =
\dfrac{1}{3} r \sum\limits_{i=1}^{n} S_{i} = \dfrac{1}{3} r S\]
当\(n\)趋于无穷大时，误差趋于\(0\)，所以\(V =
\dfrac{1}{3} r S = \dfrac{4}{3} \pi r^{3}\)，得到\(S = 4 \pi r^{2}\)。\(\Box\)
球
球也可以定义为空间中到一个定点距离不大于定长的点的集合，是圆在三维空间中的推广，因此也有一些重要的性质。
平面几何中，不共线的三点唯一确定一个圆。类似地：
不共面的四点唯一确定一个球。
证明：
存在性：如图，\(A, B, C,
D\)四点不共面，设\(\triangle
ABC\)的外心是\(O_{1}\)，\(\triangle DBC\)的外心是\(O_{2}\)，\(BC\)中点是\(E\)。在平面\(O_{1}O_{2}E\)内作两条直线\(OO_{1} \perp O_{1}E, OO_{2} \perp
O_{2}E\)，两线交于点\(O\)。因为\(O_{1},
O_{2}\)是外心，所以\(O_{1}E \perp BC,
O_{2} \perp BC\)，得到\(BC
\perp\)平面\(O_{1}O_{2}E\)。
\(OO_{1} \subset\)平面\(O_{1}O_{2}E\)，所以\(BC \perp OO_{1}\)，又\(BC \perp O_{1}E, BC \cap O_{1}E =
E\)，且\(BC, O_{1}E
\subset\)平面\(ABC\)，所以\(OO_{1} \perp\)平面\(ABC\)。由\(|O_{1}A| = |O_{1}B| =
|O_{1}C|\)可证得全等三角形，故\(|OA| =
|OB| = |OC|\)，同理\(|OD| = |OB| =
|OC|\)。这样就有\(|OA| = |OB| = |OC| =
|OD|\)，得到球\(O\)。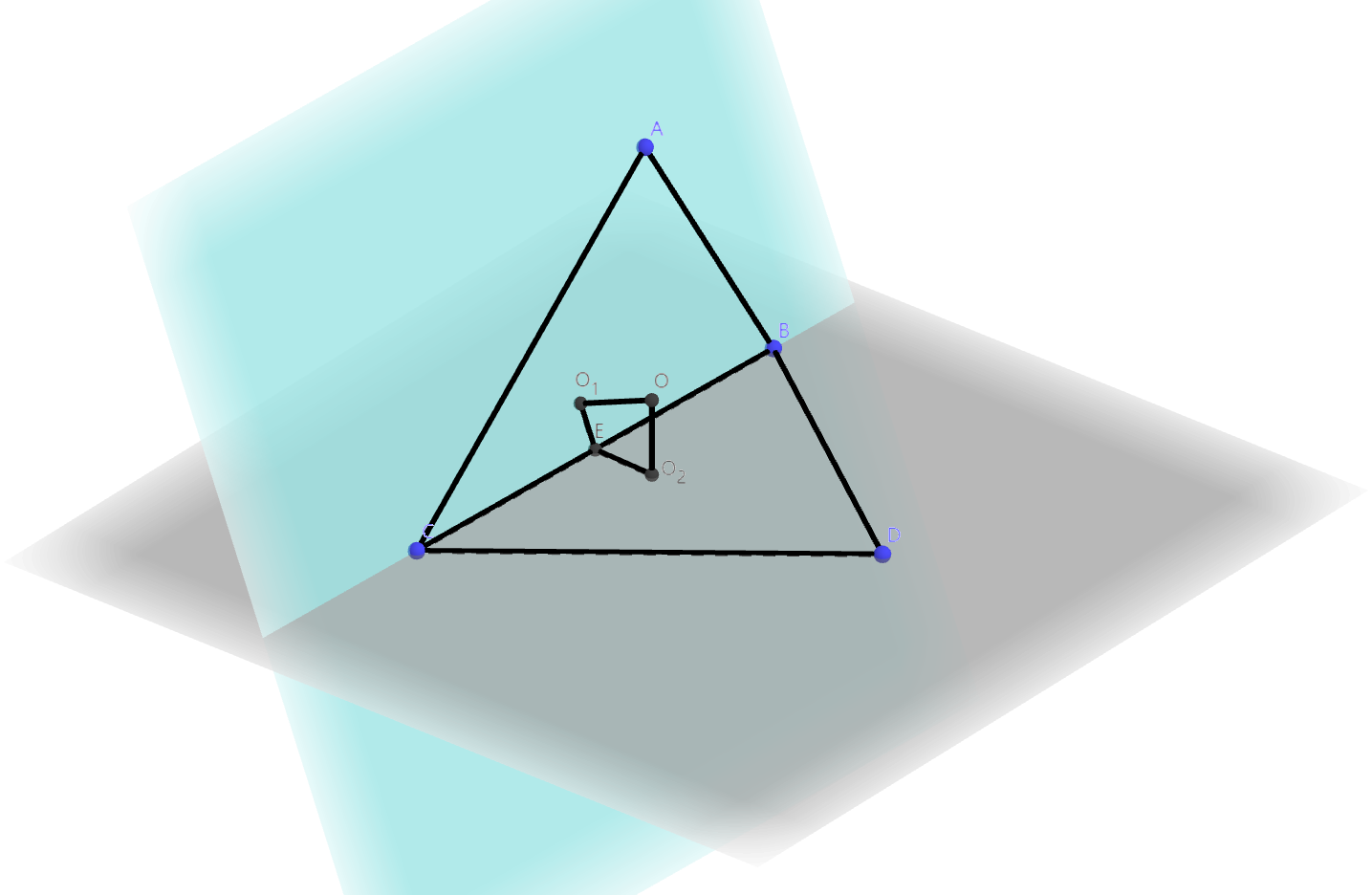 
唯一性：\(A, B, C,
D\)四点确定的球心，是由四个三角形\(ABC,
BCD, CDA,
DAB\)的外心引出的与各自平面垂直的直线交点。因为两点唯一确定一条直线，所以这样的点至多只有一个。\(\Box\)
这个球也叫四面体\(ABCD\)的外接球（circumscribed sphere），球心\(O\)叫做四面体的外心。
球被一个平面所截，如果球与平面没有交点，那么称球与平面相离；如果恰有一个交点，那么称球与平面相切，交点称为切点；如果至少有两个交点，那么称球与平面相交。球被平面所截，还有一个显而易见的重要性质：
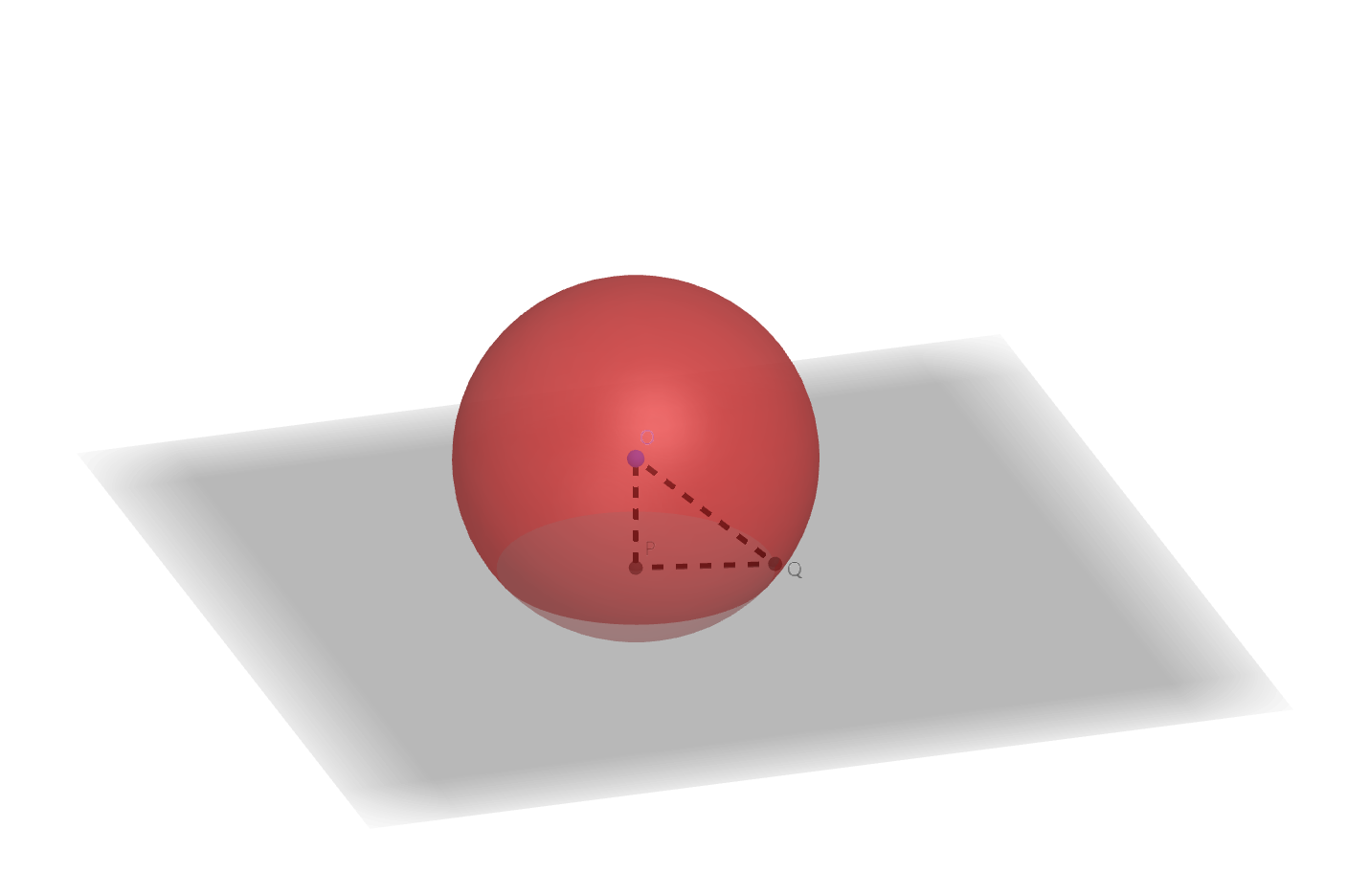
球体被任何平面所截，截面是一个圆。
证明：
如图，设球\(O\)被平面\(\alpha\)所截，球面与平面\(\alpha\)的交集为曲线\(C\)。作\(OP \perp
\alpha\)，垂足为\(P\)，并取\(Q \in C\)。因为\(PQ \subset \alpha\)，所以\(OP \perp PQ\)，由勾股定理知道\(|PQ| = \sqrt{|OQ|^{2} - |OP|^{2}} = \sqrt{r^{2} -
|OP|^{2}}\)为定值。因此\(C\)的点都在一个圆心为\(P\)，半径为\(d =
\sqrt{r^{2} - |OP|^{2}}\)的圆\(\gamma\)上。
任取点\(R \in \gamma\)，则\(|PR| = d\)。而\(OP \perp PR\)，由勾股定理知道\(|OR| = \sqrt{d^{2} + |OP|^{2}} =
r\)，所以\(R\)在球面上，也就是圆\(\gamma\)的点都在\(C\)上。由此得到\(C\)就是圆\(\gamma\)。\(\Box\)
球体被平面所截得到的圆有两种：经过圆心的圆称为大圆（great
circle），不经过圆心的圆称为小圆（small
circle）。大圆是所有截面圆中半径最大的。
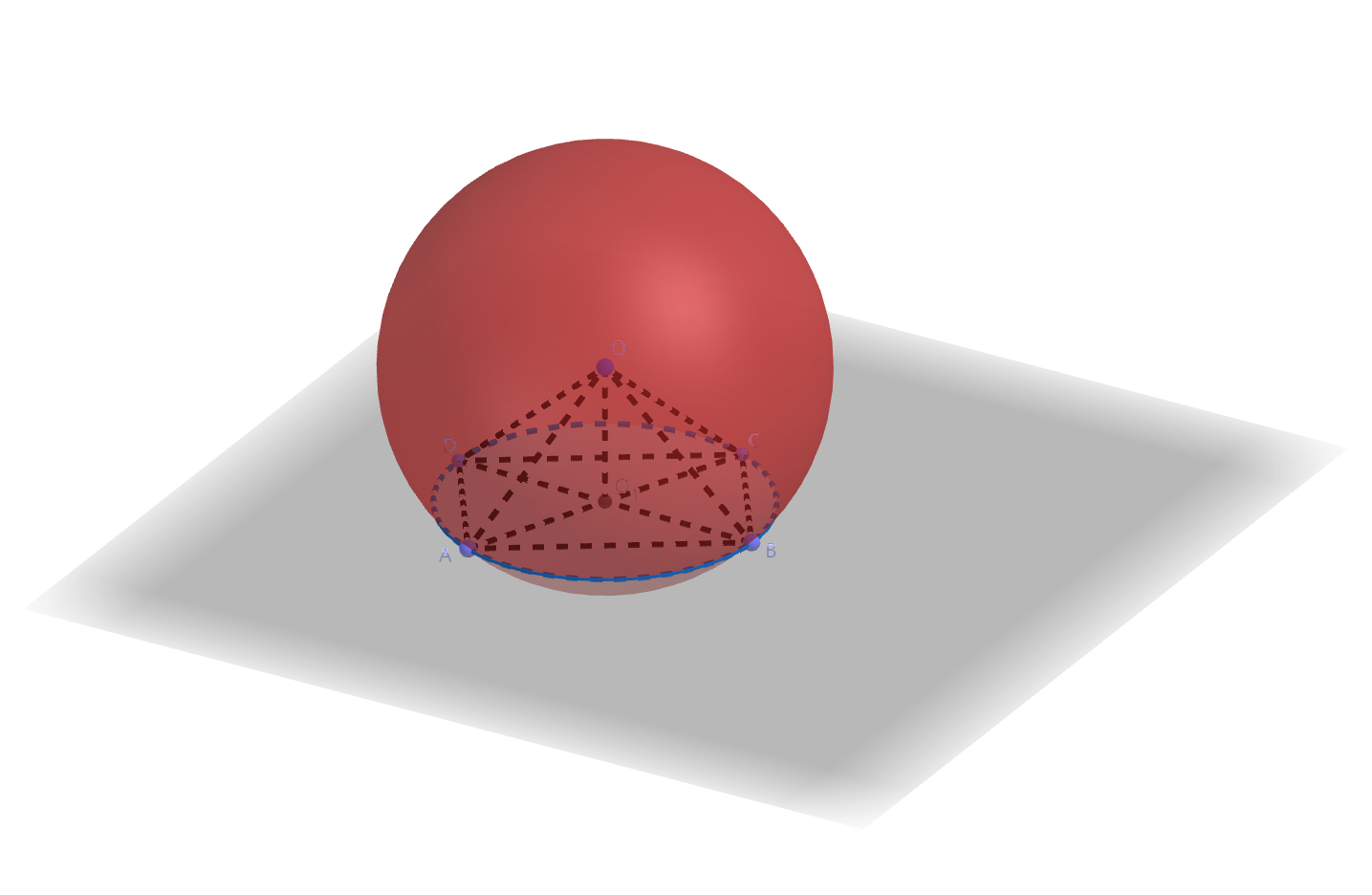
设球\(O\)的一个小圆为圆\(O_{1}\)，则\(OO_{1}\)垂直于圆\(O_{1}\)所在平面。
证明：
作圆\(O_{1}\)的内接矩形\(ABCD\)，则\(O_{1}\)为\(AC,
BD\)中点。因为\(|OA| =
|OC|\)，所以\(\triangle OO_{1}A \cong
\triangle OO_{1}C\)。所以\(\angle
OO_{1}A = \angle OO_{1}C = \dfrac{\pi}{2}\)，得到\(OO_{1} \perp AC\)，同理\(OO_{1} \perp BD\)。又\(AC \cap BD = O_{1}\)，所以\(OO_{1} \perp\)平面\(ABCD\)。\(\Box\)
类似地，有相切关系的定理：
设球\(O\)与平面\(\alpha\)相切，切点为\(P\)，则\(OP \perp
\alpha\)；
设球\(O\)与直线\(l\)相切，切点为\(P\)，则\(OP \perp
l\)。
在平面几何中，有圆的相交弦定理、切割线定理和割线定理，这三条定理都来源于圆幂定理。而在立体几何中，也有相应的球幂定理。
设球\(O\)的半径是\(r\)，\(P\)为空间中一点，我们称\(|OP|^{2} - r^{2}\)的绝对值为点\(P\)关于球\(O\)的幂：
设\(P\)是不在球\(O\)的球面上的点，过点\(P\)作直线\(l\)与球面交于两点\(A, B\)，则\(|PA|
\cdot |PB|\)等于点\(P\)关于球\(O\)的幂；
设\(P\)是不在球\(O\)的球面上的点，过点\(P\)作直线\(l\)与球面相切于点\(T\)，则\(|PT|^{2}\)等于点\(P\)关于球\(O\)的幂。
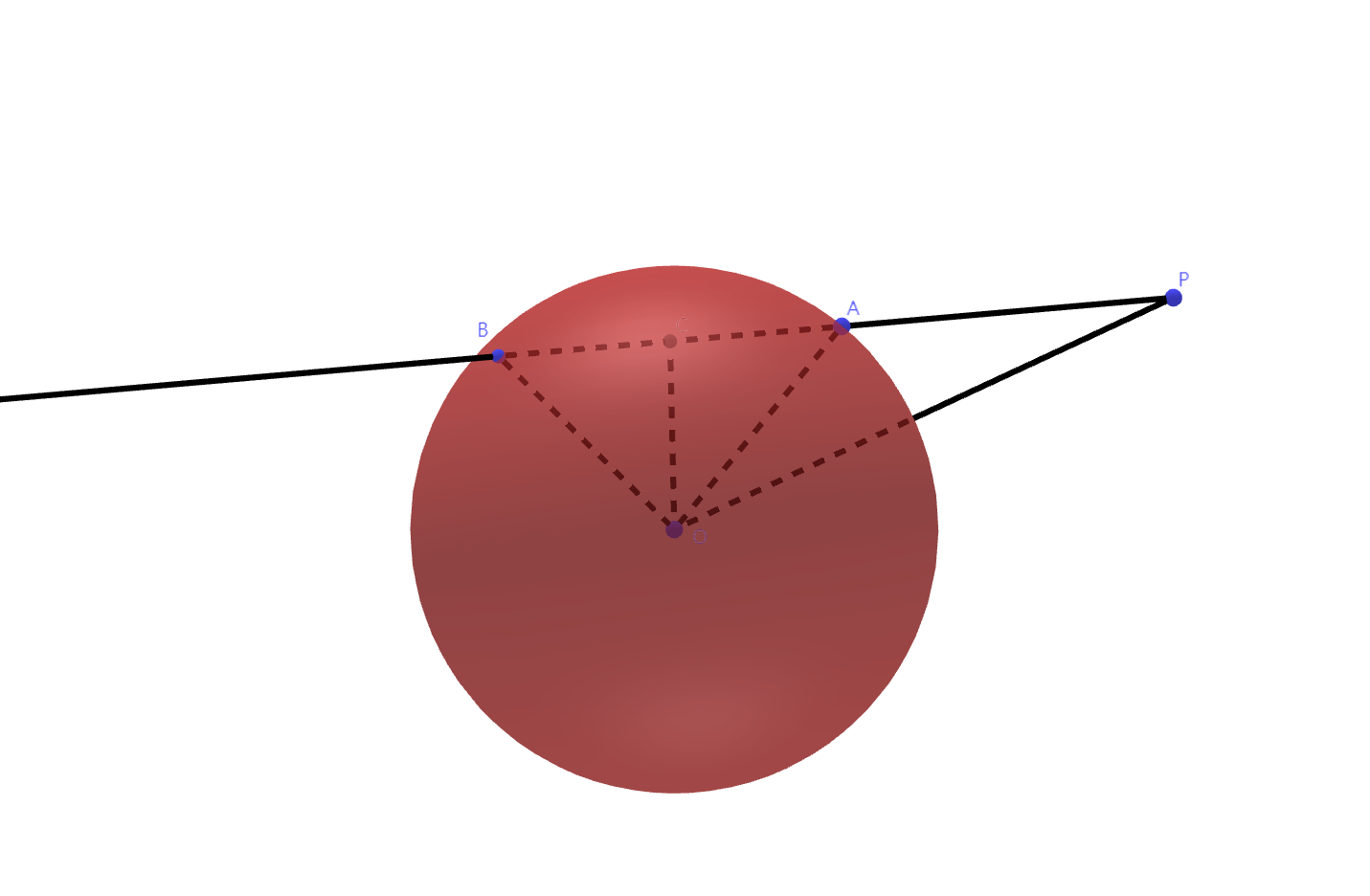证明：
设\(C\)为\(AB\)中点，易得\(OC \perp AB\)。这样， \[
\begin{align}
|PA| \cdot |PB| &= (|PC| - |AC|) (|PC| + |BC|) \\
&= |PC|^{2} - |AC|^{2} \\
&= (|OP|^{2} - |OC|^{2}) - (|OA|^{2} - |OC|^{2}) \\
&= |OP|^{2} - r^{2}
\end{align}
\] 相切时的情况证明类似。\(\Box\)
由球幂定理，就可以轻松推出球的相交弦定理、切割线定理和割线定理。
四面体
四个不共线的点两两相连，构成四个平面，这四个平面围成了一个四面体。四面体的六条棱可以分为三组对棱，每组对棱相互异面。
前面提到，四面体有一个唯一的外接球，这个外接球的球心就是四面体的外心（circumcenter）。将经过线段中点的垂面称为垂直平分面（perpendicular bisector），四面体的外心同时也是六条棱的垂直平分面的交点。
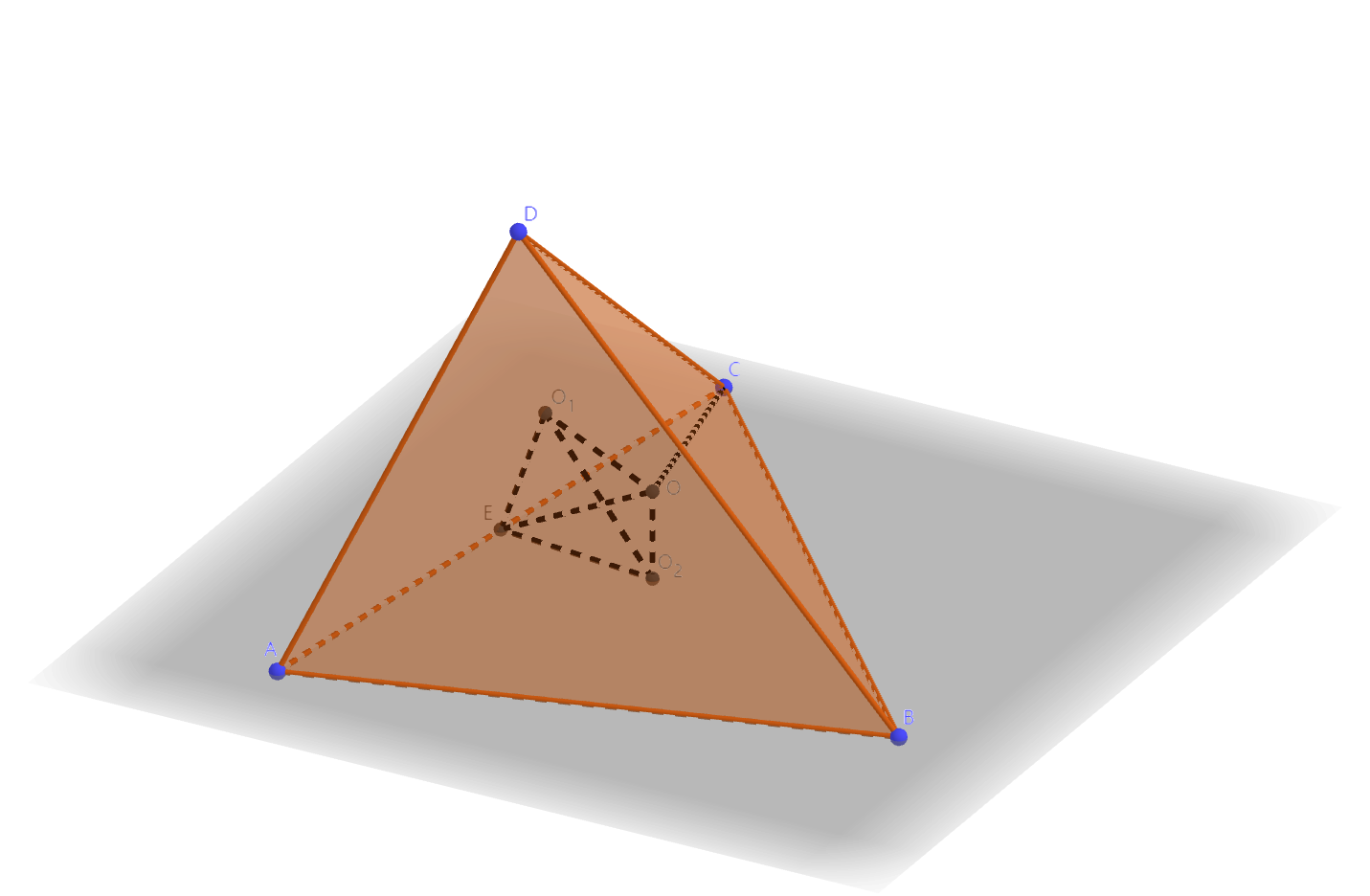如图，设四面体\(ABCD\)的外心是\(O\)，三角形\(ADC,
ABC\)的外心分别是\(O_{1},
O_{2}\)，\(AC\)中点是\(E\)，则\(O, E,
O_{1}, O_{2}\)四点共圆。用平面几何可以求出\(O_{1}E, O_{2}E\)，根据二面角\(D-AC-B\)的值可以解三角形\(O_{1}O_{2}E\)，得到圆的直径\(OE\)。最后就能得到外接球半径 \[R = |OC| = \sqrt{|OE|^{2} + |CE|^{2}} =
\sqrt{|OE|^{2} + \dfrac{1}{4} |AC|^{2}}\]
和三角形类似，四面体有外心，也自然有内心（incenter）。将经过二面角的棱，并且平分二面角的半平面称为角平分面（angle
bisector），四面体的内心就是六个角平分面的交点。
和角平分线类似，角平分面上的点到二面角的两个半平面距离相等，其逆定理同样成立。转化为平面几何就能容易证明。
由这个定理可知，三面角的三个角平分面共线。
过四面体的内心可以作一个球与四面体的四个面都相切，因此四面体的内心同时也是四面体的内切球（inscribed
sphere）的球心。总结成一个结论就是：
四面体的六个角平分面有唯一的交点，这个交点到四个面的距离相等。
这个结论的证明如下：
存在性：四面体\(ABCD\)中，\(A\)对应的三面角的三个角平分面共线\(l\)，\(l\)显然穿过\(\triangle BCD\)内部。二面角\(A-BD-C\)的角平分面经过线段\(AC\)，因此一定与\(l\)相交。设交点为\(I\)，则\(I\)到四面体的四个面距离相等。
唯一性：设点\(I\)到四面体的四个面距离相等，则\(I\)一定在六个二面角的角平分面上，也就是四个三面角对应直线的交点，这样的点至多只有一个。\(\Box\)
内心可以用于求四面体的体积。设四面体的内切球半径是\(r\)，四面体的表面积是\(S\)，则四面体的体积 \[V = \dfrac{1}{3} rS\]
用体积法可以证明：
设四面体\(ABCD\)的内心是\(I\)，则\(V =
V_{I-ABC} + V_{I-BCD} + V_{I-CDA} +
V_{I-DAB}\)。这四个三棱锥的高都是内切球半径\(r\)，因此\(V =
\dfrac{1}{3} r (S_{\triangle ABC} + S_{\triangle BCD} + S_{\triangle
CDA} + S_{\triangle DAB}) = \dfrac{1}{3} rS\)。\(\Box\)
类似可以得到角平分面的性质定理。设四面体\(ABCD\)中，二面角\(D-AB-C\)的角平分面与线段\(DC\)交于点\(E\)，则 \[\dfrac{|DE|}{|EC|} = \dfrac{S_{\triangle DAB}}{S_{\triangle ABC}}\]
将四面体的一个顶点与对面重心的连线称为四面体的中线（median），四面体的重心（centroid）就是四条中线的交点。
四面体的四条中线交于重心一点。设四面体\(D-ABC\)中，\(DP\)为一条中线，\(G\)为重心，则\(\dfrac{|DG|}{|GP|} = 3\)。
这个结论的证明如下：
如图，设四面体\(D-ABC\)中，\(D_{1}, D_{2}, D_{3}\)分别是\(AB, BC, CA\)的中点，则\(\triangle ABC\)的三条中线交于重心一点\(P\)，\(DP\)就是四面体的一条中线。设\(Q\)是\(\triangle
DBC\)的重心，则\(Q\)在\(DD_{2}\)上，\(AQ\)也是四面体的一条中线。\(DP, AQ \subset\)平面\(DAD_{2}\)，所以两条中线显然相交，设交点是\(G\)。\(G
\in\)平面\(DBD_{3}\)，则\(CG\)与平面\(DAC\)的交点在\(DD_{3}\)上，设交点是\(R\)。
在平面\(DAD_{2}\)中，过点\(P\)作\(PE
\parallel AQ\)交\(DD_{2}\)于点\(E\)，则\(\dfrac{|QE|}{|ED_{2}|} = \dfrac{|AP|}{|PD_{2}|} =
2\)，得到\(\dfrac{|DG|}{|GP|} =
\dfrac{|DQ|}{|QE|} = 3\)。
在平面\(DBD_{3}\)中，过点\(G\)作\(GF
\parallel BD_{3}\)交\(DD_{3}\)于点\(F\)，则\(\dfrac{|DF|}{|FD_{3}|} = \dfrac{|DG|}{|GP|} = 3,
\dfrac{|FG|}{|D_{3}P|} = \dfrac{|AG|}{|AP|} =
\dfrac{3}{4}\)。那么\(\dfrac{|RF|}{|RD_{3}|} = \dfrac{|FG|}{|D_{3}B|} =
\dfrac{|FG|}{|D_{3}P|} \cdot \dfrac{|D_{3}P|}{|D_{3}B|} =
\dfrac{1}{4}\)，得到\(\dfrac{|DR|}{|RD_{3}|} = 2\)。因此\(R\)为\(\triangle
DAC\)重心，\(BR\)是四面体的一条中线，三条中线交于一点。由于四面体的四个面相同，故四条中线交于一点。\(\Box\)
四面体的四条高并不一定交于一点，因此不是任何四面体都有垂心（orthocenter）。有垂心的四面体叫做垂心四面体（orthocentric
tetrahedron）。
一个四面体是垂心四面体的充要条件是：三组对棱分别垂直。
证明：
充分性：如图，在四面体\(ABCD\)中，作\(CE
\perp AB\)，垂足是\(E\)。因为\(CD
\perp AB\)，所以\(AB
\perp\)平面\(CDE\)，得到\(DE \perp AB\)。作\(AF \perp BC\)，垂足是\(F\)，同理可得\(BC
\perp\)平面\(ADF\)，于是\(DF \perp BC\)。设\(CE, AF\)交于点\(P\)，则\(P\)为\(\triangle
ABC\)的垂心。因为\(DP
\subset\)平面\(CDE\)，所以\(DP \perp AB\)，同理\(DP \perp BC\)，得到\(DP \perp\)平面\(ABC\)，是四面体的一条高。同理，作\(CG \perp BD\)，垂足为\(G\)，\(CG,
DF\)交于点\(Q\)，则\(BD \perp\)平面\(ACG\)，\(AQ\)也是四面体的一条高。此时\(DP, AQ \subset\)平面\(ADF\)，一定有交点，设交点为\(H\)。
因为\(CH \subset\)平面\(CDE\)，所以\(CH
\perp AB\)；因为\(CH
\subset\)平面\(ACG\)，所以\(CH \perp BD\)。这样得到\(CH \perp\)平面\(ABD\)，同理\(BH
\perp\)平面\(ACD\)。因此四条高交于一点，\(ABCD\)就是垂心四面体。
必要性：因为\(DP
\perp\)平面\(ABC\)，所以\(CP\)是\(CD\)在平面\(ABC\)的射影。\(CP
\perp AB\)，由三垂线定理，\(CD \perp
AB\)。同理，三组对棱分别垂直。\(\Box\)
还有进一步的定理：
若四面体的两组对棱分别垂直，则第三组对棱也垂直。
此外，从上面存在性的证明，可以得到垂心四面体的一个性质：
垂心四面体的任意一个顶点在对面的射影是对面三角形的垂心。
在棱长这一方面，垂心四面体有性质：
四面体\(ABCD\)是垂心四面体的充要条件是： \[|AB|^{2} + |CD|^{2} = |AD|^{2} + |BC|^{2} =
|AC|^{2} + |BD|^{2}\]