学习笔记·复数

复数

为了解决$x^{2} + 1 = 0$这样的方程在实数系中无解的问题，我们引入一个新数$\mathrm{i}$，使得$x = \mathrm{i}$是方程的解，即满足$\mathrm{i}^{2} = -1$。
这样，我们就能扩充数系，新数系中的所有数都可以表示为

$$z = a + b \mathrm{i} (a, b \in \mathbb{R})$$

形如这种形式的数叫做复数（complex number），其中$\mathrm{i}$叫做虚数单位（imaginary unit）。复数通常用$z, w$等字母表示。全体复数构成复数集：

$$\mathbb{C} = \{a + b \mathrm{i} | a, b \in \mathbb{R}\}$$

对于复数$z = a + b \mathrm{i} (a, b \in \mathbb{R})$，其实部（real part）为$a$，可以表示为$\operatorname{Re}(z)$或$\Re(z)$；虚部（imaginary part）为$b$，可以表示为$\operatorname{Im}(z)$或$\Im(z)$。
当且仅当$b = 0$时，$z$为实数。当$b \ne 0$时，$z$为虚数（imaginary number）；当$a = 0$且$b \ne 0$时，$z$为纯虚数。

虚数不能比较大小，只有相等和不等两种情况。两个复数相等当且仅当实部和虚部分别相等，即$a + b \mathrm{i} = c + d \mathrm{i}$当且仅当$a = c$且$b = d$，$a, b, c, d \in \mathbb{R}$。

复数的几何意义

任何一个复数$z = a + b \mathrm{i} (a, b \in \mathbb{R})$都可以由一个有序实数对$(a, b)$唯一确定，因此，复数可以和向量建立双射，$\{1, \mathrm{i}\}$就是一组基。
建立平面直角坐标系，把$x$轴称为实轴（real axis），$y$轴称为虚轴（imaginary axis）。这样，平面内每个点$P(a, b)$都能对应一个向量$\overrightarrow{OP} = (a, b)$，并同时对应一个复数$z = a + b \mathrm{i}$。这个平面称为复平面（complex plane）。
显然，实轴上的点都表示实数；除了原点外，虚轴上的点都表示纯虚数。虚数单位$\mathrm{i}$就是$(0, 1)$。

对于复平面内的向量$\overrightarrow{OZ} = (a, b)$，$\overrightarrow{OZ}$的模$|\overrightarrow{OZ}|$即为复数$z = a + b \mathrm{i}$的模（modulus），记为$|z|$：

$$|z| = |a + b \mathrm{i}| = \sqrt{a^{2} + b^{2}}$$

关于模，显然有不等式：

$$|\operatorname{Re}(z)| \le |z|, |\operatorname{Im}(z)| \le |z|$$

定义$z = a + b \mathrm{i} (a, b \in \mathbb{R})$的共轭复数（complex conjugate）

$$\bar{z} = a - b \mathrm{i}$$

共轭复数的实部相等，虚部互为相反数。在复平面内，共轭复数关于实轴对称。

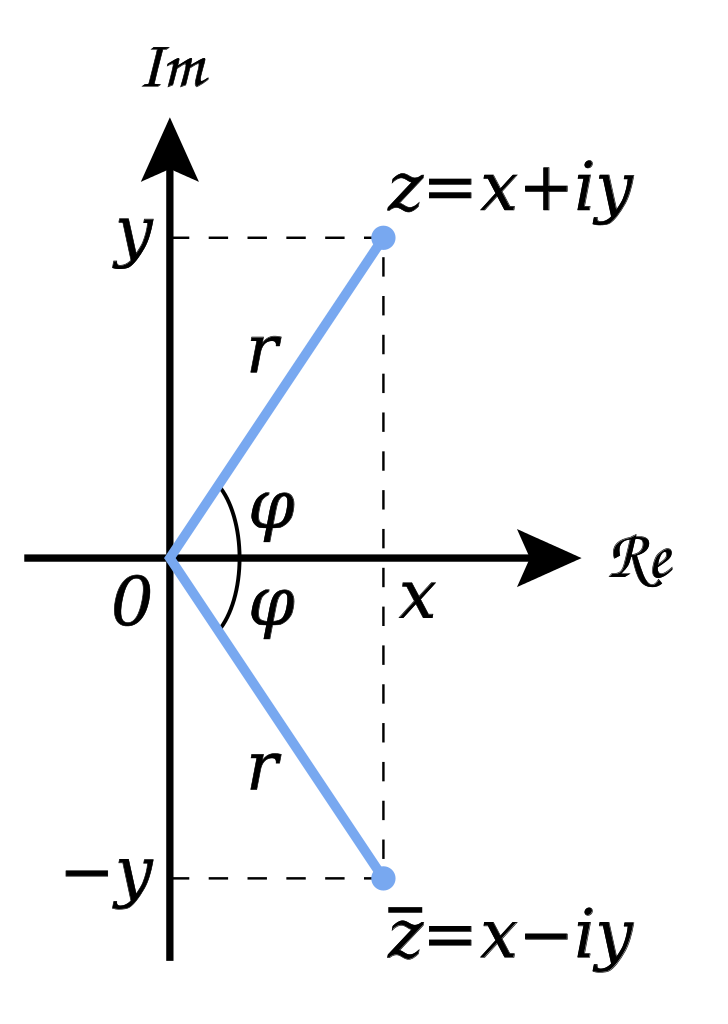
显然，$|z| = |\bar{z}|$，$\bar{\bar{z}} = z$。

复数的运算

设复数$z_{1} = a + b \mathrm{i}, z_{2} = c + d \mathrm{i} (a, b, c, d \in \mathbb{R})$，定义复数的加法：

$$z_{1} + z_{2} = (a + c) + (b + d) \mathrm{i}$$

定义复数的减法为加法的逆运算：

$$z_{1} - z_{2} = (a - c) + (b - d) \mathrm{i}$$

容易得到，复数的加减法是满足交换律和结合律的。

复数的乘法：

$$z_{1} z_{2} = (ac - bd) + (ad + bc) \mathrm{i}$$

这可以由$\mathrm{i}^{2} = -1$得到：

$$\begin{align} z_{1} z_{2} &= ac + a (d \mathrm{i}) + (b \mathrm{i}) c + (b \mathrm{i}) (d \mathrm{i}) \\ &= ac + (ad + bc) \mathrm{i} + bd \mathrm{i}^{2} \\ &= (ac - bd) + (ad + bc) \mathrm{i} \quad \Box \end{align}$$

乘法同样满足交换律、结合律，并满足分配律。

可以看出，复数的加法和乘法可以像多项式一样计算，“合并同类项”。
复数的加法、减法和数乘实际上与坐标表示的向量的计算是一样的。

定义非零复数$z = a + b \mathrm{i} (a, b \in \mathbb{R})$的倒数$\dfrac{1}{z}$，满足$z \cdot \dfrac{1}{z} = 1$。通过解方程组，可以得到$\dfrac{1}{z}$是唯一确定的复数：

$$\dfrac{1}{z} = \dfrac{a}{a^{2} + b^{2}} - \dfrac{b}{a^{2} + b^{2}} \mathrm{i}$$

那么，设复数$z_{1} = a + b \mathrm{i}, z_{2} = c + d \mathrm{i} (a, b, c, d \in \mathbb{R}, c + d \mathrm{i} \ne 0)$，定义复数的除法：

$$\dfrac{z_{1}}{z_{2}} = \dfrac{ac + bd}{c^{2} + d^{2}} + \dfrac{bc - ad}{c^{2} + d^{2}} \mathrm{i}$$

复数的除法也可以看作是$\dfrac{a + b \mathrm{i}}{c + d \mathrm{i}}$的分子与分母同乘分母的共轭复数，从而使分母“实数化”：

$$\begin{align} \dfrac{z_{1}}{z_{2}} &= \dfrac{a + b \mathrm{i}}{c + d \mathrm{i}} \\ &= \dfrac{(a + b \mathrm{i}) (c - d \mathrm{i})}{(c + d \mathrm{i}) (c - d \mathrm{i})} \\ &= \dfrac{(ac + bd) + (bc - ad) \mathrm{i}}{c^{2} + d^{2}} \\ &= \dfrac{ac + bd}{c^{2} + d^{2}} + \dfrac{bc - ad}{c^{2} + d^{2}} \mathrm{i} \end{align}$$

除法$\dfrac{z_{1}}{z_{2}}$有时也可以写作$z_{1} \div z_{2}$。

复数的整数次幂与实数的意义是相同的，$z^{n} (n \in \mathbb{N}^{\ast})$即代表自乘$n$次，而$z^{-n} = \dfrac{1}{z^{n}}, z^{0} = 1 (z \ne 0)$。

关于共轭复数，有以下几个简单的定理：

$$\begin{align} & z \cdot \bar{z} = |z|^{2} \\ & \operatorname{Re}(z) = \dfrac{1}{2} (z + \bar{z}), \operatorname{Im}(z) = \dfrac{1}{2 \mathrm{i}} (z - \bar{z}) \\ & \bar{z} + \bar{w} = \overline{z + w}, \bar{z} \cdot \bar{w} = \overline{z w}, \dfrac{\bar{z}}{\bar{w}} = \overline{\dfrac{z}{w}} \end{align}$$

由此可以得到推论：

$$|zw| = |z| \cdot |w|, |\dfrac{z}{w}| = \dfrac{|z|}{|w|}$$

类似向量的三角不等式，复数也有模不等式：

$$||z| - |w|| \le |z + w| \le |z| + |w|$$

不用向量的方法，也可以用复数来证明：

$$\begin{align} |z + w|^{2} &= (z + w) (\overline{z + w}) \\ &= (z + w) (\bar{z} + \bar{w}) \\ &= z \bar{z} + (z \bar{w} + w \bar{z}) + w \bar{w} \\ &= |z|^{2} + 2 \operatorname{Re}(z \bar{w}) + |w|^{2} \\ &\le |z|^{2} + 2 |z| |w| + |w|^{2} \\ &= (|z| + |w|)^{2} \end{align}$$

开方就得到右边，同理可得左边。$\Box$

复数的三角形式

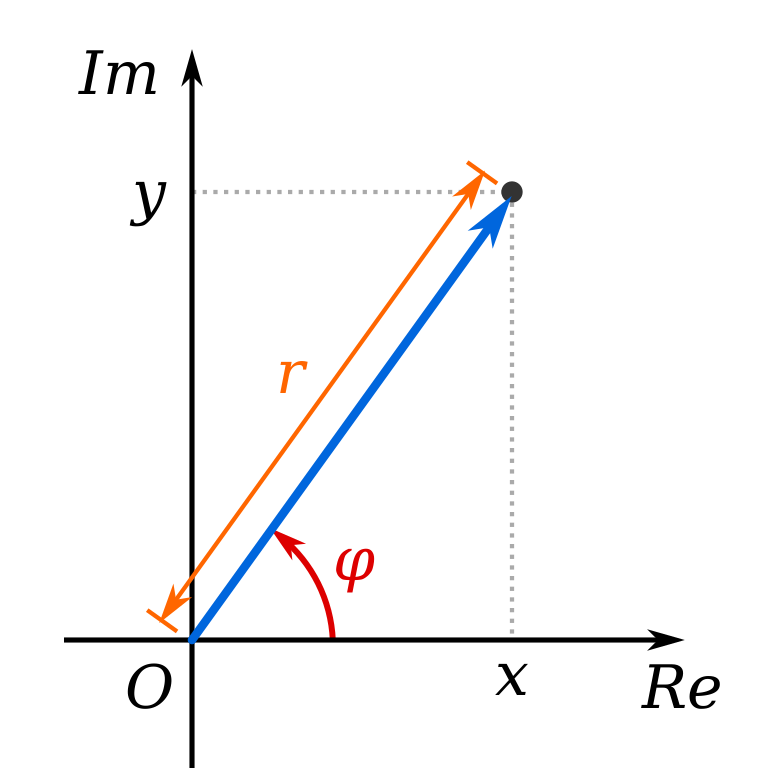
设非零复数$z$在复平面内对应一个点$Z$，$|z| = r$，则$|\overrightarrow{OZ}| = r$。设$\theta$为以射线$OZ$为终边的角，那么点$Z(r \cos \theta, r \sin \theta)$，也就是

$$z = r (\cos \theta + \mathrm{i} \sin \theta)$$

这个形式称为复数的三角形式，其中$\theta$称为复数$z$的辐角（argument）。显然，辐角有无穷多个，但可以找到$\theta_{0} \in [0, 2 \pi)$，使得对任意辐角都有

$$\theta = \theta_{0} + 2k \pi, k \in \mathbb{Z}$$

$\theta_{0}$称为复数$z$的辐角主值（principal value of an argument），通常记为$\arg z$。

为了与三角形式区分，$a + b \mathrm{i}$称为复数的代数形式。

一般情况下，设非零复数$z = a + b \mathrm{i}$，其辐角$\theta$满足

$$\cos \theta = \dfrac{a}{a^{2} + b^{2}}, \sin \theta = \dfrac{b}{a^{2} + b^{2}}$$

因此，两个复数相等等价于模和辐角主值分别相等。

欧拉公式（Euler’s formula）有：

$$\mathrm{e}^{\mathrm{i} \theta} = \cos \theta + \mathrm{i} \sin \theta$$

那么，复数就能表示为

$$z = r \mathrm{e}^{\mathrm{i} \theta}$$

这个形式称为复数的指数形式。

复数乘除运算的三角表示

设复数$z_{1} = r_{1} (\cos \theta + \mathrm{i} \sin \theta), z_{2} = r_{2} (\cos \varphi + \mathrm{i} \sin \varphi)$，计算两个复数的乘法，根据三角函数公式有：

$$\begin{align} z_{1} z_{2} &= r_{1} r_{2} (\cos \theta + \mathrm{i} \sin \theta) (\cos \varphi + \mathrm{i} \sin \varphi) \\ &= r_{1} r_{2} ((\cos \theta \cos \varphi - \sin \theta \sin \varphi) + \mathrm{i} (\sin \theta \cos \varphi + \cos \theta \sin \varphi)) \\ &= r_{1} r_{2} (\cos(\theta + \varphi) + \mathrm{i} \sin(\theta + \varphi)) \end{align}$$

这就是说，两个复数相乘，模相乘，辐角相加。用指数形式表示就是：

$$r_{1} \mathrm{e}^{\mathrm{i} \theta} \cdot r_{2} \mathrm{e}^{\mathrm{i} \varphi} = r_{1} r_{2} \mathrm{e}^{\mathrm{i} (\theta + \varphi)}$$

这样是符合指数运算规律的。

在复平面内，我们可以发现复数乘法$z_{1} z_{2}$的几何意义，就是把$z_{1}$对应的向量的模变为原来的$r_{2}$倍，并逆时针旋转$\varphi$。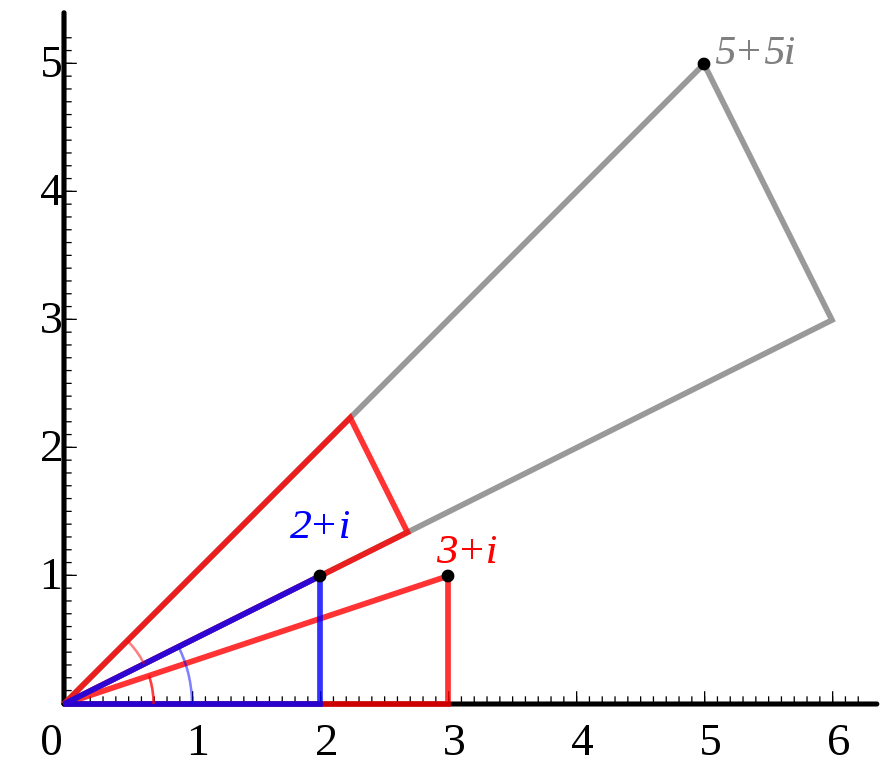

由此可以发现，复数能表达旋转变换。对于实数$\theta$，映射$f(z) = \mathrm{e}^{\mathrm{i} \theta} z$的几何意义就是把$z$对应的向量旋转角$\theta$。

那么，复数的除法就是

$$\dfrac{z_{1}}{z_{2}} = \dfrac{r_{1} (\cos \theta + \mathrm{i} \sin \theta)}{r_{2} (\cos \varphi + \mathrm{i} \sin \varphi)} = \dfrac{r_{1}}{r_{2}} (\cos(\theta - \varphi) + \mathrm{i} \sin(\theta - \varphi))$$

这样，两个复数相除，模相除，辐角相减。用指数形式表示就是：

$$\dfrac{r_{1} \mathrm{e}^{\mathrm{i} \theta}}{r_{2} \mathrm{e}^{\mathrm{i} \varphi}} = \dfrac{r_{1}}{r_{2}} \mathrm{e}^{\mathrm{i} (\theta - \varphi)}$$

除法的几何意义就与乘法相反，$\dfrac{z_{1}}{z_{2}}$表示把$z_{1}$对应的向量的模变为原来的$\dfrac{1}{r_{2}}$并顺时针旋转$\varphi$所得到的向量对应的复数。

复数的开方

设复数$z = \mathrm{e}^{\mathrm{i} \theta}$，按照指数的运算规律计算，有

$$z^{n} = (\mathrm{e}^{\mathrm{i} \theta})^{n} = \mathrm{e}^{\mathrm{i} (n \theta)}$$

这样就得到了棣莫弗定理（de Moivre’s theorem）：

$$(\cos \theta + \mathrm{i} \sin \theta)^{n} = \cos(n \theta) + \mathrm{i} \sin(n \theta)$$

设$z$为复数，$n \in \mathbb{N}^{\ast}$，若复数$w$满足$w^{n} = z$，则称$w$为$z$的一个$n$次方根。这样，就能求复数的开方了。
设非零复数$z = r (\cos \theta + \mathrm{i} \sin \theta), w = \rho (\cos \varphi + \mathrm{i} \sin \varphi)$，其中$\theta, \varphi$都是辐角主值。根据棣莫弗定理，

$$w^{n} = \rho^{n} (\cos(n \varphi) + \mathrm{i} \sin(n \varphi))$$

再由$w^{n} = z$，得$\rho^{n} = r \Rightarrow \rho = r^{\frac{1}{n}}$和$n \varphi = \theta + 2k \pi \Rightarrow \varphi = \dfrac{\theta + 2k \pi}{n}, k \in \mathbb{Z}$。这样，

$$0 \le \dfrac{\theta + 2k \pi}{n} < 2 \pi \Rightarrow -\dfrac{\theta}{2 \pi} \le k < n - \dfrac{\theta}{2 \pi} \Rightarrow -1 < k < n$$

所以$k \in \{0, 1, \cdots, n - 1\}$。

这样，就能得到非零复数$z = r (\cos \theta + \mathrm{i} \sin \theta) (\theta \in [0, 2 \pi))$有$n$个$n$次方根：

$$w_{k} = r^{\frac{1}{n}} (\cos \dfrac{\theta + 2k \pi}{n} + \mathrm{i} \sin \dfrac{\theta + 2k \pi}{n}), k = 0, 1, \cdots, n - 1$$

特别地，$1$的$n$次方根，即一元$n$次方程$x^{n} = 1$的$n$个根，分别是：

$$\xi_{k} = \cos \dfrac{2k \pi}{n} + \mathrm{i} \sin \dfrac{2k \pi}{n} = \mathrm{e}^{\mathrm{i} \frac{2k \pi}{n}}, k = 0, 1, \cdots, n - 1$$

$\xi_{0} = 1$，就是实数情形下的平凡解。
$\xi_{0}, \xi_{1}, \cdots, \xi_{n - 1}$称为$n$次单位根（root of unity），由定义都满足$\xi_{k}^{n} = 1$。

令$\xi = \xi_{1} = \mathrm{e}^{\mathrm{i} \frac{2 \pi}{n}}$，根据棣莫弗定理，

$$\xi_{k} = \xi^{k}, k = 0, 1, \cdots, n - 1$$

$\xi^{n} = 1$，那么$\xi^{k} (k \in \mathbb{Z})$就是周期变化的。根据后面的因式定理，

$$x^{n} - 1 = \prod_{k=0}^{n - 1} (x - \xi_{k}) = \prod_{k=0}^{n - 1} (x - \xi^{k})$$

画图可知，所有的$n$次单位根在复平面内对应的点组成一个正$n$边形。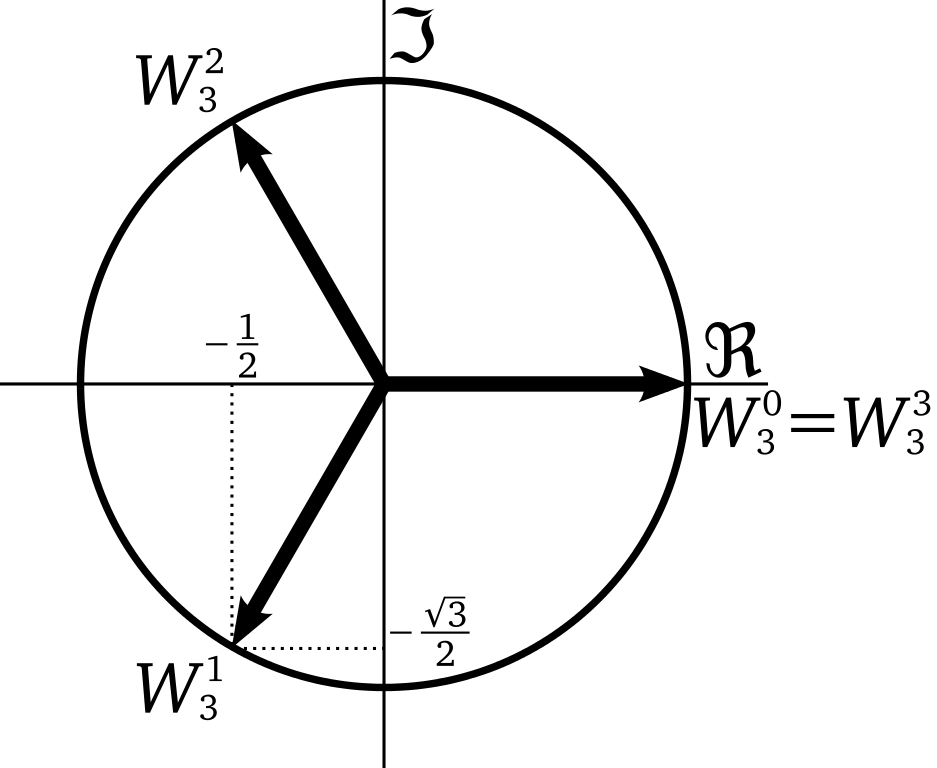

根据恒等式

$$x^{n} - 1 = (x - 1) (x^{n - 1} + x^{n - 2} + \cdots + 1)$$

只要$k \ne 0$，就有$\xi_{k} \ne 1$，这样，

$$0 = \xi_{k}^{n} - 1 = (\xi_{k} - 1) (\xi_{k}^{n - 1} + \xi_{k}^{n - 2} + \cdots + 1)$$

得到

$$\xi_{k}^{n - 1} + \xi_{k}^{n - 2} + \cdots + 1 = 0$$

特别地，令$k = 1$，得到

$$\xi^{n - 1} + \xi^{n - 2} + \cdots + 1 = 0$$

由$\xi_{k} = \xi^{k}$，这个式子用求和符号表示就是

$$\sum\limits_{k=0}^{n - 1} \xi_{k} = 0$$

复数与方程

一元二次方程

对于方程$a x^{2} + b x + c = 0 (a, b, c \in \mathbb{C}, a \ne 0)$，配方得到：

$$(x + \dfrac{b}{2a})^{2} = \dfrac{b^{2} - 4ac}{4 a^{2}}$$

对判别式$b^{2} - 4ac$开方。设开方得到的两个结果为$d_{1, 2}$，那么方程的根

$$x_{1, 2} = \dfrac{d_{1, 2} - b}{2a}$$

根据复数的开方公式，可以得到$d_{1} + d_{2} = 0$。把其中一个记为$\sqrt{b^{2} - 4ac}$，就能得到熟悉的求根公式：

$$x_{1, 2} = \dfrac{-b \pm \sqrt{b^{2} - 4ac}}{2a}$$

如果限定系数范围为$a, b, c \in \mathbb{R}$，那么

1. 若$b^{2} - 4ac > 0$，方程有两个不相等的实根；
2. 若$b^{2} - 4ac = 0$，方程有两个相等的实根；
3. 若$b^{2} - 4ac < 0$，方程有两个共轭虚根： $$x_{1, 2} = \dfrac{-b \pm \sqrt{4ac - b^{2}} \mathrm{i}}{2a}$$

一元$n$次方程

代数基本定理（fundamental theorem of algebra）：
任何一元$n (n \in \mathbb{N}^{\ast})$次复系数多项式方程$f(x) = 0$至少有一个复数根。

复系数多项式，是指形如$\sum\limits_{k=0}^{n} a_{k} x^{k} (a_{k} \in \mathbb{C})$的式子，最高次非零项的次数就是多项式的次数。$0$称为零多项式，不定义次数。
这个定理有很多种证明，但都涉及高等数学知识，这里不作介绍。

设$a$为复数，$f(x)$为复系数多项式，因式定理（factor theorem）有：
$a$为$f(x)$的根当且仅当$(x - a)$为$f(x)$的一个因式。

证明如下：
充分性：如果$(x - a)$为$f(x)$的一个因式，那么$f(x) = (x - a) g(x)$，其中$g(x)$为复系数多项式。从而可以得到$f(a) = (a - a) g(a) = 0$。
必要性：如果$f(a) = 0$，设$f(x) = \sum\limits_{k=0}^{n} c_{k} x^{k}, c_{k} \in \mathbb{C}$，那么

$$\begin{align} f(x) &= f(x) - f(a) \\ &= \sum\limits_{k=0}^{n} c_{k} x^{k} - \sum\limits_{k=0}^{n} c_{k} a^{k} \\ &= \sum\limits_{k=0}^{n} c_{k} (x^{k} - a^{k}) \\ &= (x - a) \left(\sum\limits_{k=1}^{n} c_{k} (x^{k - 1} + x^{k - 2} a + \cdots + a^{k - 1}) \right) \quad \Box \end{align}$$

若正整数$k$满足$(x - a)^{k}$为$f(x)$的因式，但$(x - a)^{k + 1}$不为$f(x)$的因式，则称$a$为$f(x)$的$k$重根。二重及以上的根称为重根。
这样，就能由上面两个定理得到推论：
任何一元$n (n \in \mathbb{N}^{\ast})$次复系数多项式方程$f(x) = 0$都有$n$个复数根（重根按重数计，即把$k$重根当作$k$个根来计）。

把重根合到一起就得到唯一分解定理（unique factorization theorem）：
任何一元$n (n \in \mathbb{N}^{\ast})$次复系数多项式都可以唯一地表示为

$$f(x) = a \prod_{k=1}^{m} (x - a_{k})^{f_{k}}$$

其中$a, a_{1}, \cdots, a_{m} \in \mathbb{C}, f_{1}, f_{2}, \cdots, f_{m} \in \mathbb{N}^{\ast}$，满足$\sum\limits_{k=1}^{m} f_{k} = n$。

这样，设$f(x) = \sum\limits_{k=0}^{n} a_{k} x^{k} (a_{n} \ne 0)$的根为$x_{1}, x_{2}, \cdots, x_{n}$，$f(x)$就可以表示成：

$$f(x) = a_{n} (x - x_{1}) (x - x_{2}) \cdots (x - x_{n})$$

展开多项式就能得到韦达定理（Vieta’s formulas）：

$$\sum\limits_{1 \le i_{1} < i_{2} < \cdots < i_{k} \le n} x_{i_{1}} x_{i_{2}} \cdots x_{i_{k}} = (-1)^{k} \dfrac{a_{n} - k}{a_{n}}, k = 1, 2, \cdots, n$$

这个式子实际上就等价于

$$\begin{cases} x_{1} + x_{2} + \cdots + x_{n} = -\dfrac{a_{n - 1}}{a_{n}} \\ (x_{1} x_{2} + x_{1} x_{3} + \cdots + x_{1} x_{n}) + (x_{2} x_{3} + x_{2} x_{4} + \cdots + x_{2} x_{n}) + \cdots + x_{n - 1} x_{n} = \dfrac{a_{n - 2}}{a_{n}} \\ \quad \vdots \\ x_{1} x_{2} \cdots x_{n} = (-1)^{n} \dfrac{a_{0}}{a_{n}} \end{cases}$$

例如，设一元三次方程$a x^{3} + b x^{2} + c x + d = 0$的三个根（计重数）分别为$x_{1}, x_{2}, x_{3}$，则

$$\begin{align} a x^{3} + b x^{2} + c x + d &= a (x - x_{1}) (x - x_{2}) (x - x_{3}) \\ &= a x^{3} - a (x_{1} + x_{2} + x_{3}) x^{2} + a (x_{1} x_{2} + x_{2} x_{3} + x_{3} x_{1}) x - x_{1} x_{2} x_{3} \end{align}$$

比对系数可得三次方程的韦达定理：

$$\begin{cases} x_{1} + x_{2} + x_{3} = -\dfrac{b}{a} \\ x_{1} x_{2} + x_{2} x_{3} + x_{3} x_{1} = \dfrac{c}{a} \\ x_{1} x_{2} x_{3} = -\dfrac{d}{a} \end{cases}$$

对于实系数多项式，即系数都是实数的多项式，有虚根成对定理：
若复数$a$是实系数多项式$f(x)$的根，则$\bar{a}$也是$f(x)$的根。

要证明这个定理，需要用到一个引理：对于任何实系数多项式$f$和复数$z$有$\overline{f(z)} = f(\bar{z})$。这个引理的证明如下：

$$\begin{align} & \quad f(x) = \sum\limits_{k=0}^{n} a_{k} x^{k}, a_{k} \in \mathbb{R} \\ &\Rightarrow a_{k} = \overline{a_{k}} \\ &\Rightarrow \overline{f(z)} = \overline{\sum\limits_{k=0}^{n} a_{k} z^{k}} = \sum\limits_{k=0}^{n} a_{k} \bar{z}^{k} = f(\bar{z}) \end{align}$$

这时，因为$f(a) = 0$，所以$f(\bar{a}) = \overline{f(a)} = 0$。$\Box$

这样，实系数多项式的根，除去实根以外，就都是成对的共轭复数。一元$n (n \in \mathbb{N}^{\ast})$次实系数多项式就能在实数范围内分解为：

$$f(x) = a \prod_{k=1}^{s} (x - a_{k}) \cdot \prod_{k=1}^{t} (x^{2} + b_{k} x + c_{k})$$

其中$a, a_{k}, b_{k}, c_{k} \in \mathbb{R}$，$s + 2t = n$，且$c_{k} > 0, b_{k}^{2} < 4 c_{k}$。