学习笔记·逻辑与集合
逻辑
谓词逻辑
谓词逻辑(predicate
logic)是数理逻辑的基础。谓词(predicate)是表示性质或关系的词,通常用大写字母\(P, Q,
R\)等来表示,而谓词描述的对象称为主词(subject)。例如,设\(P\)表示「考了100分」,\(x\)表示「小刚」,那么命题「小刚考了100分」可以记作\(P(x)\),其中\(P\)就是谓词,\(x\)就是主词。
有时,我们需要对主词限定范围,进行量化。表示量化的词称为量词(quantifier)。最基本的两种量词是全称量词(universal
quantifier)和存在量词(existential
quantifier)。
全称量词符号为\(\forall\),用于表示「任意」(for
all)这样的词。例如「所有小朋友\(x\)都考了100分」,可以表示为\(\forall x, P(x)\)。
存在量词符号为\(\exists\),用于表示「存在」(there
exists)这样的词。例如「至少有一个小朋友\(x\)考了100分」,可以表示为\(\exists x, P(x)\)。
命题逻辑
谓词和主词构成了原子命题(atomic
formula),即不可再分的简单命题。从命题出发,就进入了更为基础的命题逻辑(propositional
logic)。
命题(proposition)是陈述句所表达的判断,不涉及谓词时,通常用小写字母\(p, q,
r\)等表示。一般情况下,我们说命题非真(true,
T)即假(false,
F),这里的真和假表示的就是命题的真值(truth
value)。
原子命题之间可以用逻辑联结词(logical connective)连接起来,构成复合命题。
与(合取;conjunction)和或(析取;disjunction)是最常见的两个联结词,一般用符号\(\land\)和\(\lor\)来表示。(不是非法符号!)
例如,设\(p\)表示「小刚考了100分」,\(q\)表示「小强考了100分」,那么\(p \land q\)表示「他们都考了100分」,\(p \lor
q\)表示「他们之中有人考了100分」。
我们可以用真值表(truth table)来计算复合命题的真值:
| \(p\) | \(q\) | \(p \land q\) |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
| \(p\) | \(q\) | \(p \lor q\) |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
容易看出,\(p, q\)同时为真时\(p \land q\)为真,而\(p, q\)只要有一为真时\(p \lor q\)为真。
与和或满足:
- 交换律:\(p \land q = q
\land p\)
\(p \lor q = p \lor q\) - 结合律:\((p \land q)
\land r = p \land (q \land r)\)
\((p \lor q) \lor r = p \lor (q \lor r)\) - 分配律:\(p \land (q \lor
r) = (p \land q) \lor (p \land r)\)
\(p \lor (q \land r) = (p \lor q) \land (p \lor r)\) - 幂等律:\(p \land p = p \lor p = p\)
非(否定;negation)用于否定命题,符号为\(\lnot\)。
非的真值表如下:
| \(p\) | \(\lnot p\) |
|---|---|
| T | F |
| F | T |
不难证明: \[\begin{align} & \lnot (p \land q) = \lnot p \lor \lnot q \\ & \lnot (p \lor q) = \lnot p \land \lnot q \end{align}\] 即反演律,也称德·摩根定律(De Morgan’s laws)。
此外,条件(conditional)联结词也在数学证明中被大量用到,也称蕴涵(implication),符号为\(\to\),但在具体的数学推理中一般使用\(\Rightarrow\)。条件联结词可以写成「若\(p\),则\(q\)」(if \(p\), then \(q\))的形式,其中\(p\)称为前件(antecedent),\(q\)称为后件(consequent)。
\(p \to q\)等价于\(\lnot p \lor
q\),由此可以计算出蕴涵的真值表:
| \(p\) | \(q\) | \(p \to q\) |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
若命题\(p \to q\)为真,则称\(p\)为\(q\)的充分条件(sufficient condition),\(q\)为\(p\)的必要条件(necessary condition)。
对于命题\(p \to
q\),其否命题为\(\lnot
p \to \lnot q\),逆命题为\(q \to p\),逆否命题为\(\lnot q \to \lnot
p\)。其中原命题与其逆否命题是等价的,证明如下:
由定义,\(\lnot q \to \lnot p = \lnot (\lnot
q) \lor \lnot p = \lnot p \lor q = p \to q\)。\(\Box\)
双条件(biconditional)联结词,即等价(equivalence),符号为\(\leftrightarrow\)或\(\Leftrightarrow\),可以写成「\(p\)当且仅当\(q\)」(\(p\) if and only if \(q\), \(p\)
iff \(q\))的形式。
\(p \leftrightarrow q\)等价于\((p \to q) \land (q \to p)\),此时\(p, q\)互为充要条件(sufficient and
necessary condition)。
双条件联结词的真值表:
| \(p\) | \(q\) | \(p \leftrightarrow q\) |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
根据真值表最后一列的真值情况,复合命题可以分为三类:
- 永真式或重言式(tautology):最后一列全是T,符号为\(\top\)。如\(p \lor \lnot p\)和\(p \to p\)等。
- 矛盾式(contradiction):最后一列全是F,符号为\(\bot\)。如\(p \land \lnot p\)等。
- 或然式(contingency):最后一列既存在T也存在F。
设所有元素为\(x_{1}, \cdots, x_{n}\),那么对于全称命题\(\forall x, P(x)\),实际上表示的是\(P(x_{1}) \land P(x_{2}) \land \cdots \land P(x_{n})\),即这些命题中每个都是真的。因此不难得出全称命题的否定: \[\lnot (\forall x, P(x)) = \exists x, \lnot P(x)\]
同样,存在命题\(\exists x,
P(x)\)表示\(P(x_{1}) \lor P(x_{2}) \lor
\cdots \lor P(x_{n})\),即至少有一个是真的。
那么 \[\lnot (\exists x, P(x)) = \forall x,
\lnot P(x)\] 这样,只要证明\(\forall x,
\lnot P(x) \Rightarrow \bot\),就能证明原命题了。
三段论(syllogism)是最经典的逻辑推理,由大前提、小前提和结论组成,例如亚里士多德(Aristotle,前384—前322)给出的这段经典推理:
- 大前提:所有人都会死
- 小前提:所有希腊人都是人
- 结论:所有希腊人都会死
设\(P(x)\)表示「\(x\)是人」,\(Q(x)\)表示「\(x\)会死」,\(R(x)\)表示「\(x\)是希腊人」,那么上述推理可以表示为: \[(\forall x, P(x) \to Q(x)) \land (\forall x, R(x) \to P(x)) \Rightarrow \forall x, R(x) \to Q(x)\]
这就是三段论最基本的形式: \[\forall x, (P(x) \to Q(x)) \land (R(x) \to P(x)) \to (R(x) \to Q(x)) = \top\]
证明如下:
假设\(\forall x, P(x) \to Q(x)\)和\(\forall x, R(x) \to P(x)\)成立,那么 \[\begin{align}
& \quad \forall x, (P(x) \to Q(x)) \land (R(x) \to P(x)) \\
&= \forall x, (\lnot P(x) \lor Q(x)) \land (\lnot R(x) \lor P(x)) \\
&= \forall x, (\lnot P(x) \land \lnot R(x)) \lor (\lnot P(x) \land
P(x)) \lor (Q(x) \land \lnot R(x)) \lor (Q(x) \land P(x)) \\
&= \forall x, (\lnot P(x) \land \lnot R(x)) \lor (Q(x) \land (\lnot
R(x) \lor P(x))) \\
&= \forall x, (\lnot P(x) \land \lnot R(x)) \lor Q(x) \\
&= \forall x, (\lnot P(x) \lor Q) \land (\lnot R(x) \lor Q(x)) \\
&= \forall x, \lnot R(x) \lor Q(x)
\end{align}\] 那么\(\forall x, R(x) \to
Q(x)\)也成立。\(\Box\)
集合
集合(set)是一系列对象的总体,这些构成集合的对象称为元素(element)。
集合通常用大写字母如\(A, B,
C\)等来表示,而元素通常用小写字母如\(a,
b, c\)等来表示。
如果元素\(x\)在集合\(A\)内,称\(x\)属于\(A\),记作\(x \in
A\);否则称\(x\)不属于\(A\),记作\(x
\notin A\)。
若两个集合\(A,
B\)中的元素完全相同,即\(\forall x, x
\in A \Leftrightarrow x \in B\),则二者相等,记作\(A = B\)。
集合可以用在大括号中列举其元素的方式来表示,即列举法(roster notation): \[\{1, 2, 3, 4, 5\}\] 对于元素较多或具有无限元素的集合,如果具有明显的规律,可以使用省略号\(\cdots\)。例如前100个正整数: \[\{1, 2, \cdots, 100\}\] 自然数集: \[\mathbb{N} = \{0, 1, 2, \cdots\}\]
无限制概括公理模式(axiom schema of unrestricted
comprehension)有:
对于任意谓词\(P\),都有 \[\exists A, \forall x, x \in A \Leftrightarrow
P(x)\] 也就是说,任意谓词\(P\)都可以确定一个集合\(A\),使得\(A\)的元素正好是所有满足\(P\)的主词。这个公理模式有严重的问题,但在大多数情况下仍然可以使用。
这个公理模式允许我们用一个谓词来表示集合,即描述法(set-builder
notation):\(\{x |
P(x)\}\)。通常需要用一个全集\(U\)来限定元素的范围,即\(\{x | x \in U \land P(x)\}\),此时\(U\)可以写在左边:\(\{x \in U | P(x)\}\)。例如\(1\)到\(5\)之间的整数: \[\{x \in \mathbb{Z} | 1 \le x \le 5\}\]
左边还可以写更复杂的表达式:\(\{f(x) |
P(x)\}\)。例如非负偶数集: \[\{2n | n
\in \mathbb{N}\}\]
集合具有以下三个性质:
- 无序性:集合中的元素没有顺序,可以任意排列
- 互异性:集合中任意两个元素都不相同,每个元素只能出现一次
- 确定性:对于一个集合,一个元素属于或不属于该集合是确定的,不能模棱两可
集合间的关系
若\(\forall x, x \in A \Rightarrow x \in
B\),则称\(A\)是\(B\)的子集(subset),\(B\)是\(A\)的超集(superset),记作\(A \subseteq B\)或\(B \supseteq A\),也称\(A\)包含于\(B\)或\(B\)包含\(A\)。
若\(A \subseteq B \land A \ne
B\),即\(\exists x, x \in B \land x
\notin A\),则称\(A\)是\(B\)的真子集(proper
subset),\(B\)是\(A\)的真超集(proper
superset),记作\(A \subsetneqq
B\)(\(A \subset B\))或\(B \supsetneqq A\)(\(B \supset A\)),也称\(A\)真包含于\(B\)或\(B\)真包含\(A\)。
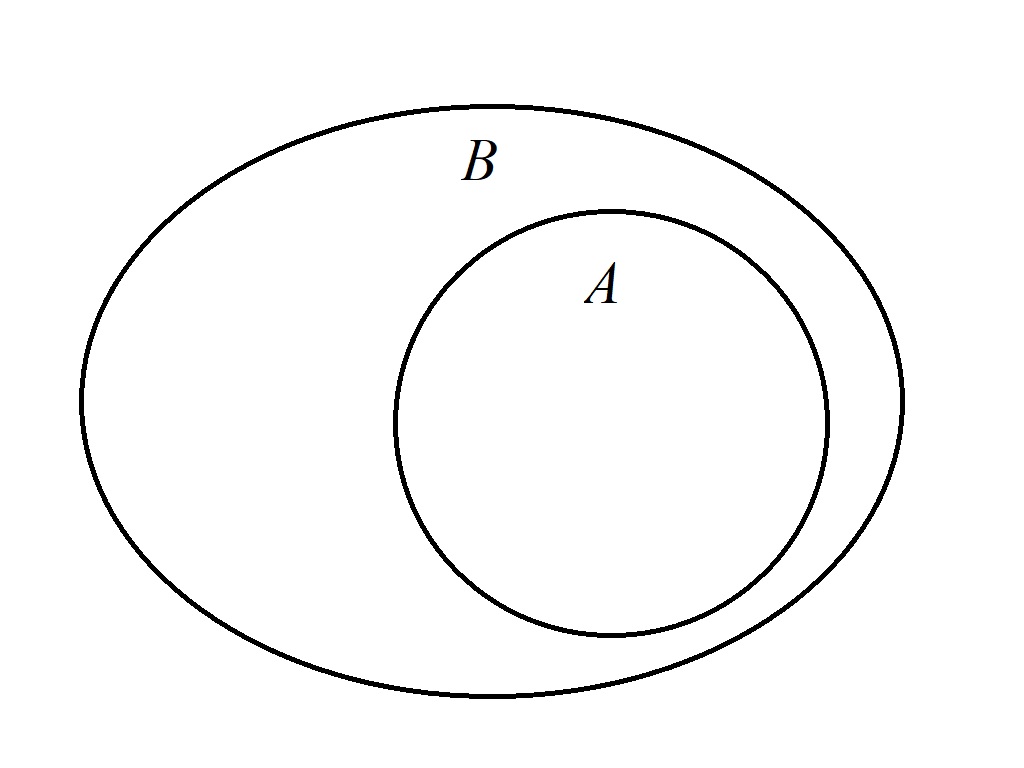
集合也可以通过Venn图(维恩图;Venn diagram)形象地表示出来。例如下图就表示\(A\)是\(B\)的子集:
包含关系具有以下三个性质:
- 自反性:\(A \subseteq A\)
- 反对称性:\(A \subseteq B \land B \subseteq A \Leftrightarrow A = B\)
- 传递性:\(A \subseteq B \land B \subseteq C \Rightarrow A \subseteq C\)
真包含关系同样具有传递性。
不含任何元素的集合称为空集(empty set),符号为\(\varnothing\)或\(\emptyset\)。
空集有基本性质: \[\forall A, \varnothing
\subseteq A\] 这是一个可证明的定理,证明如下:
证明\(\varnothing \subseteq
A\)只要证明\(x \in \varnothing
\Rightarrow x \in A\),其逆否命题为\(x
\notin A \Rightarrow x \notin
\varnothing\)。根据空集的定义以及蕴涵的真值表,这是真的。\(\Box\)
由这个性质不难得出: \[\forall A \ne
\varnothing, \varnothing \subsetneqq A\]
英国哲学家、数学家罗素(Bertrand
Russell,1872—1970)在1901年发现,无限制概括公理模式会导致一个严重的悖论:设集合\(R\)为以所有不含自身的集合为元素的集合,即\(R = \{x | x \notin x\}\),如果\(R\)以自身为元素,那么根据\(R\)的定义,\(R\)就不以自身为元素;如果\(R\)不以自身为元素,那么\(R\)作为以所有不含自身的集合为元素的集合,应当是自身的元素,即\(R \in R \Leftrightarrow R \notin
R\)。罗素悖论(Russell’s
paradox)要求数学家必须对概括公理模式进行限制,于是有限制概括公理模式(axiom
schema of restricted comprehension):
对于任意谓词\(P\),都有 \[\forall A, \exists B, \forall x, x \in B
\Leftrightarrow x \in A \land P(x)\] 也就是说,对于任意谓词\(P\),给定一个集合\(A\),都可以确定一个集合\(B\),使得\(B\)是\(A\)的子集,且\(B\)的元素正好是\(A\)中所有满足\(P\)的主词。
限制概括公理模式可以用于证明空集的存在。设\(A\)为任意非空集合,那么空集可以构造为 \[\varnothing = \{x \in A | x \in x \land x \notin x\}\]
特殊集合
数系的集合通常有专门的符号:
\(\mathbb{N}\)表示自然数集,\(\mathbb{N}^{\ast}\)表示正整数集,\(\mathbb{Z}\)表示整数集,\(\mathbb{Q}\)表示有理数集,\(\mathbb{R}\)表示实数集,\(\mathbb{C}\)表示复数集。
\[\mathbb{N}^{\ast} \subsetneqq \mathbb{N}
\subsetneqq \mathbb{Z} \subsetneqq \mathbb{Q} \subsetneqq \mathbb{R}
\subsetneqq \mathbb{C}\]
此外,还有一种特殊的实数集称为区间(interval),有时用字母\(I\)来表示:(\(a,
b \in \mathbb{R}\)且\(a <
b\)) \[\begin{align}
[a, b] &= \{x \in \mathbb{R} | a \le x \le b\} \\
(a, b) &= \{x \in \mathbb{R} | a < x < b\} \\
[a, b) &= \{x \in \mathbb{R} | a \le x < b\} \\
(a, b] &= \{x \in \mathbb{R} | a < x \le b\}
\end{align}\]
以上区间分别是闭区间、开区间、左闭右开区间和左开右闭区间。这些都是有界区间。
\(a\)和\(b\)为区间的端点,区间的长度为\(b - a\),中点为\(\dfrac{a + b}{2}\)。
用符号\(+\infty\)和\(-\infty\)表示正无穷大和负无穷大:
\[\begin{align}
[a, +\infty) &= \{x \in \mathbb{R} | x \ge a\} \\
(a, +\infty) &= \{x \in \mathbb{R} | x > a\} \\
(-\infty, b] &= \{x \in \mathbb{R} | x \le b\} \\
(-\infty, b) &= \{x \in \mathbb{R} | x < b\}
\end{align}\] 特殊地,\((-\infty,
+\infty) = \mathbb{R}\)。
含有符号\(\infty\)的区间称为无界区间。
集合的运算
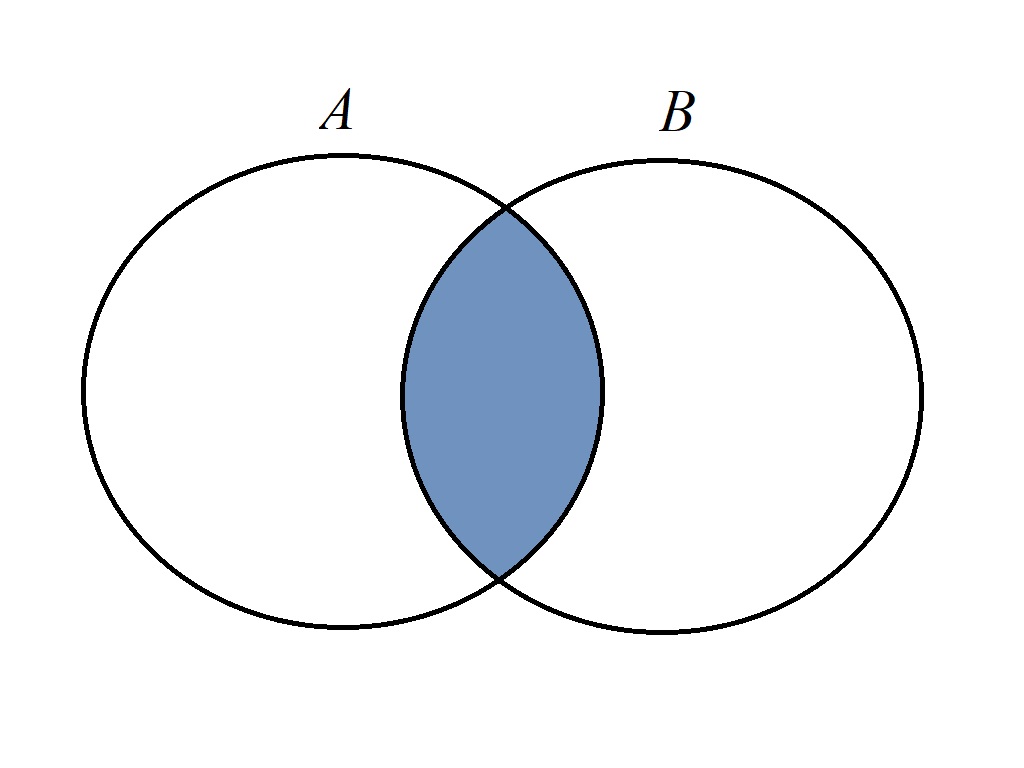
对于两个集合\(A, B\),其交集(intersection)定义为: \[A \cap B = \{x | x \in A \land x \in B\}\] 即两个集合共同拥有的元素构成的集合。
容易得到, \[A \cap B = A \Leftrightarrow A \subseteq B\]
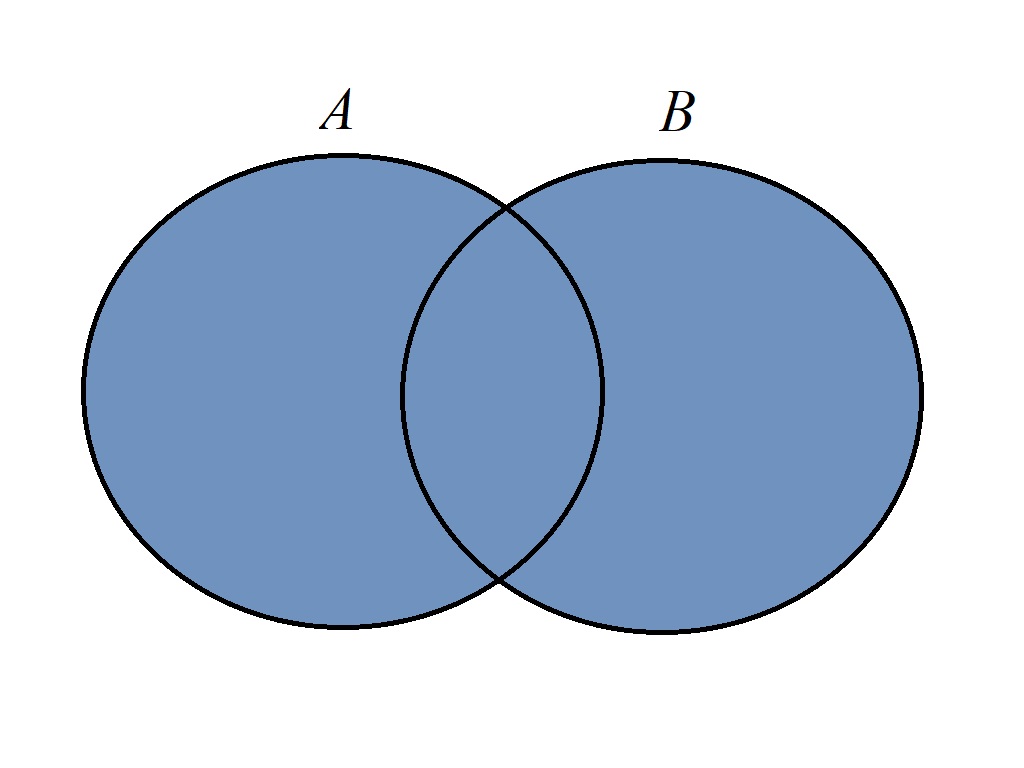
对于两个集合\(A, B\),其并集(union)定义为: \[A \cup B = \{x | x \in A \lor x \in B\}\] 即两个集合中的所有元素构成的集合。
\[A \cup B = B \Leftrightarrow A \subseteq B\]
与逻辑与和逻辑或运算类似,交集和并集也具有以下性质:
- 交换律:\(A \cap B = B
\cap A\)
\(A \cup B = B \cup A\) - 结合律:\((A \cap B) \cap
C = A \cap (B \cap C)\)
\((A \cup B) \cup C = A \cup (B \cup C)\) - 分配律:\(A \cap (B \cup
C) = (A \cap B) \cup (A \cap C)\)
\(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\) - 幂等律:\(A \cap A = A \cup A = A\)
对于空集\(\varnothing\),交集和并集还满足: \[\begin{align} & A \cap \varnothing = \varnothing \\ & A \cup \varnothing = A \end{align}\]
对于两个集合\(A, B\),\(A\)在\(B\)中的差集(set difference)或相对补集(relative complement)定义为: \[B \setminus A = \{x \in B | x \notin A\}\] 即一个集合拥有而另一个集合没有的元素构成的集合。\(B \setminus A\)也记作\(B - A\)。
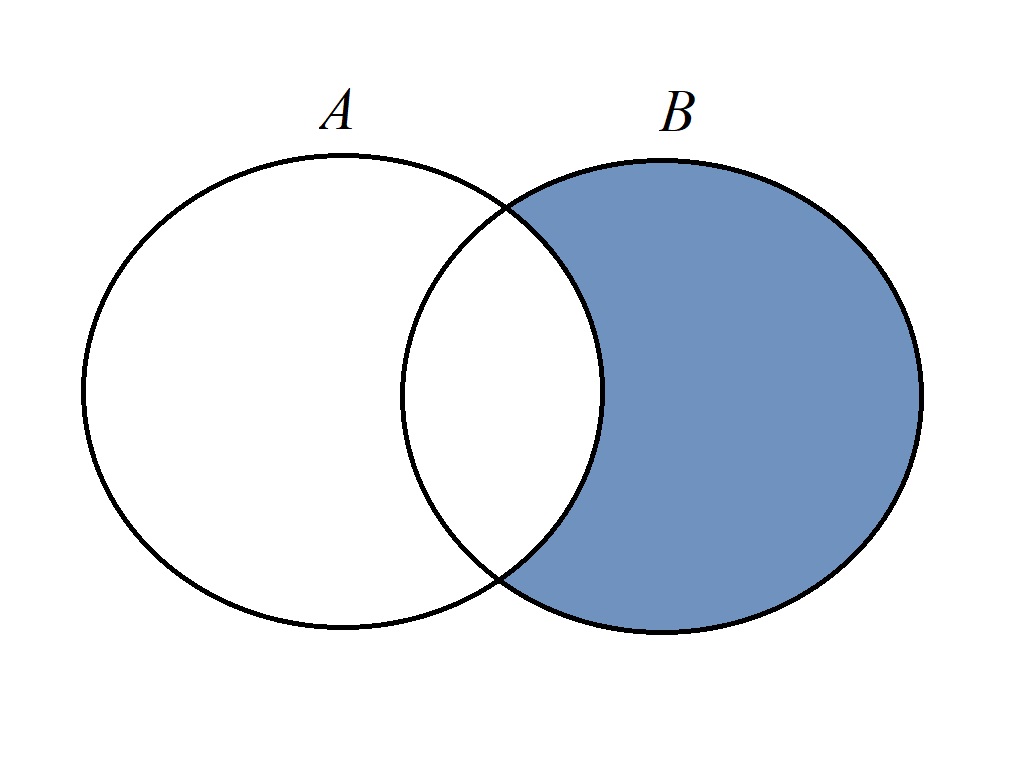
补集(complement)是一种特殊的差集,有时也称绝对补集(absolute
complement)。
在研究问题时,所有的研究对象构成的集合被称为全集(universe)。对于全集\(U\)的子集\(A\),其补集定义为: \[\complement_{U} A = U - A = \{x \in U | x \notin
A\}\] 在不产生歧义的情况下,\(\complement_{U} A\)也可以表示为\(A^{C}\)。
\[A - B = \varnothing \Leftrightarrow \complement_{U} B \subseteq \complement_{U} A \Leftrightarrow A \subseteq B\]
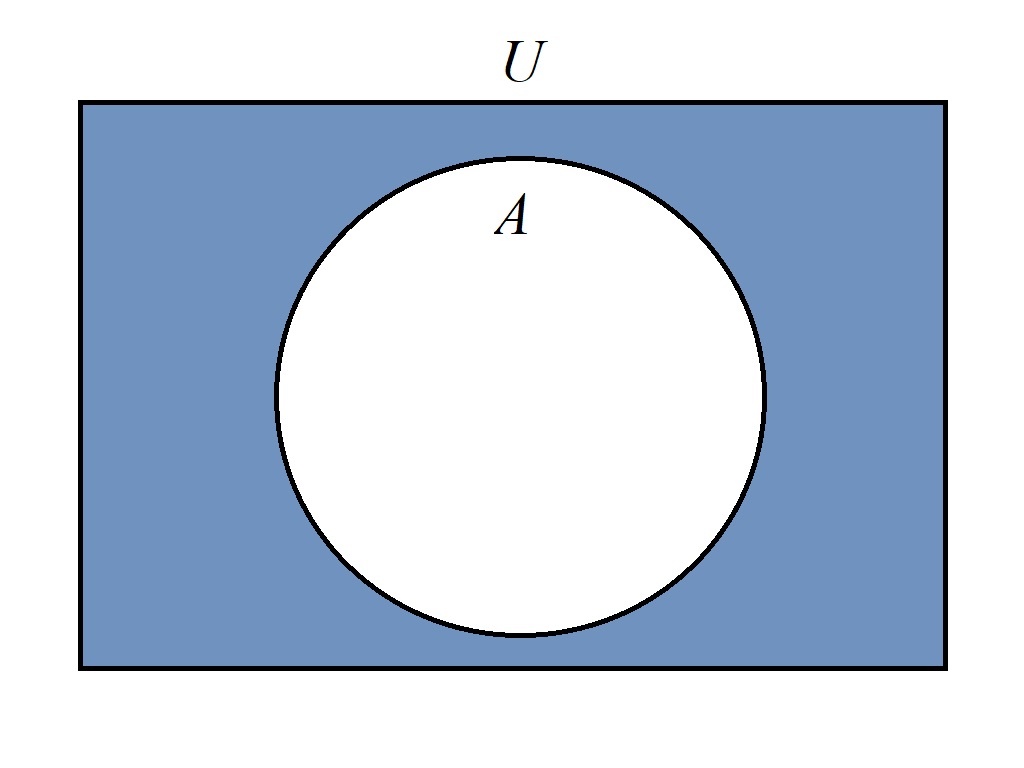
由前面的\(\lnot (p \land q) = \lnot p \lor \lnot q, \lnot (p \lor q) = \lnot p \land \lnot q\)可以推出反演律/德·摩根定律: \[\begin{align} & \complement_{U} (A \cap B) = \complement_{U} A \cup \complement_{U} B \\ & \complement_{U} (A \cup B) = \complement_{U} A \cap \complement_{U} B \end{align}\]
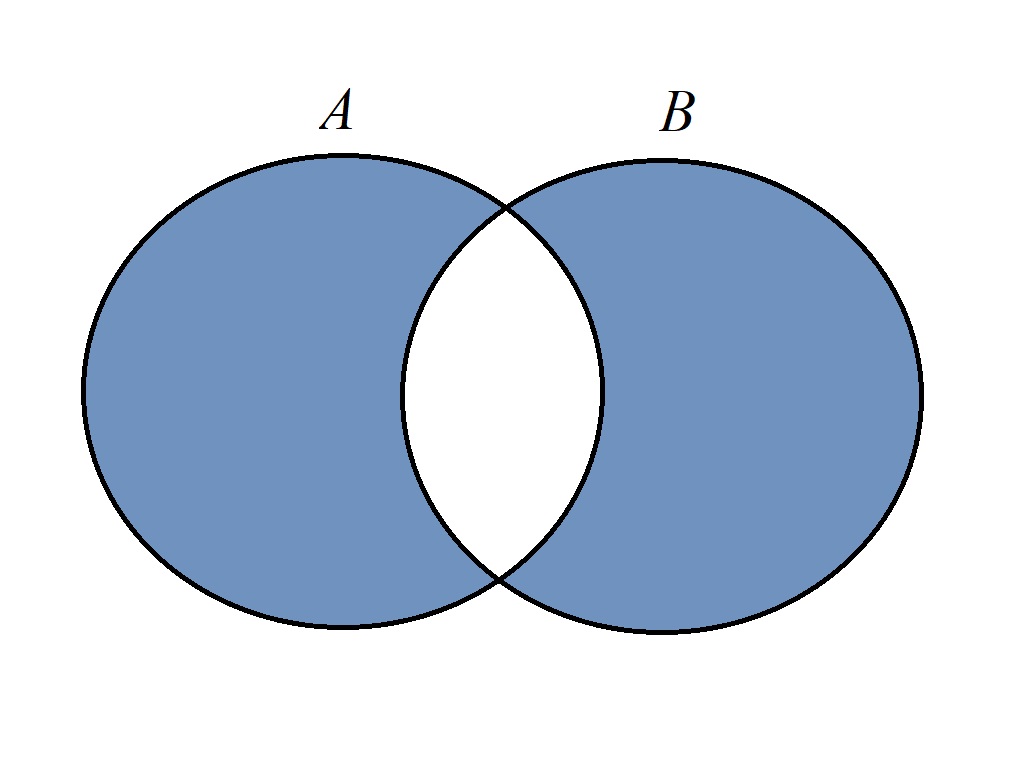
对于两个集合\(A, B\),其对称差(symmetric difference)定义为: \[A \bigtriangleup B = (A - B) \cup (B - A)\] 或 \[A \bigtriangleup B = (A \cup B) - (A \cap B)\] 即只属于其中一个集合的元素构成的集合。
对于两个集合\(A, B\),其笛卡尔积(Cartesian product)或直积定义为: \[A \times B = \{(a, b) | a \in A \land b \in B\}\] 例如,集合\(R\)是13个元素的点数集合\(\{A, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K\}\),\(S\)是4个元素的花色集合\(\{\clubsuit, \diamondsuit, \heartsuit, \spadesuit\}\),那么\(R \times S\)就是52个元素的一副标准扑克牌的集合\(\{(A, \clubsuit), (A, \diamondsuit), \cdots, (K, \heartsuit), (K, \spadesuit)\}\)。注意,笛卡尔积不满足交换律,这个集合与\(S \times R\)得到的\(\{(\clubsuit, A), (\diamondsuit, A), \cdots, (\heartsuit, K), (\spadesuit, K)\}\)是完全不同的,二者甚至不相交。
集合的势
一个集合中的元素个数可以用势(cardinality)或基数(cardinal
number)的概念表示。集合\(A\)的势或基数记作\(|A|\)或\(\mathrm{card}(A)\)。
势和基数一般是同义词。本章一律使用势来表示集合的大小。
有限集合的势
顾名思义,有限集合(finite
set)就是指元素个数有限的集合。有限集合的严格定义需要用到映射:若存在自然数\(n\)以及双射\(f: A
\to \{1, 2, \cdots, n\}\),则\(A\)为有限集合。
有限集合的势就是其元素个数\(n\),其中空集的势为\(0\)。例如集合\(A
= \{-3, 0, 2, 7, 9\}\),则\(|A| =
5\)。
容斥原理(inclusion–exclusion
principle)是组合计数(enumerative
combinatorics)中的基本原理之一,表述为 \[|A \cup B| = |A| + |B| - |A \cap B|\]
从Venn图上可以很直观地理解这个原理。 
容斥原理还可以推广到三个乃至更多集合之间: \[|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B|
- |A \cap C| - |B \cap C| + |A \cap B \cap C|\]
可以理解为三个集合相交的部分计算了三次,减去所有两两相交的部分又多减了一次,因此加回三者相交的部分。
对于更多的集合,先将单个集合的势相加,然后减去所有两个集合相交的部分,再加回所有三个集合相交的部分,再减去所有四个集合相交的部分,依此类推。
集合的幂集(power
set)是该集合全部子集构成的集合。对于集合\(S\),其幂集\(\mathcal{P}(S)\)可以表示为: \[\mathcal{P}(S) = \{x | x \subseteq S\}\]
\(S\)的幂集也可以记作\(2^{S}\)。
例如,集合\(S = \{a, b,
c\}\),那么\(S\)的幂集 \[\mathcal{P}(S) = \{\varnothing, \{a\}, \{b\},
\{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\}\}\]
幂集的实质就是考虑集合\(S\)中每一个元素选或不选,每一种选择构成一个集合,因此可以得出
\[|S| = n, |\mathcal{P}(S)| =
2^{n}\]
无限集合的势
不是有限集合的集合就是无限集合(infinite
set)。
若两个集合\(A, B\)之间存在双射\(f: A \to
B\),则称这两个集合等势(equinumerous)。
对于自然数集\(\mathbb{N}\),其势定义为\(\aleph_{0}\),读作阿列夫零(aleph-naught/-zero/-null)。若集合\(A\)与\(\mathbb{N}\)等势,则称\(A\)为可数集(countable
set),\(|A| =
\aleph_{0}\)。可数集和有限集统称至多可数集合(at most
countable set)。
设集合\(S\),若存在单射\(f: S \to \mathbb{N}\)或满射\(g: \mathbb{N} \to S\),则\(S\)为至多可数集合。
至多可数集合的子集都是至多可数集合,可以通过将第\(n\)个元素映射到自然数\(n\)上证明。
类似地,我们也能证明\(\mathbb{Z}\)和\(\mathbb{Q}\)都是可数集,即使它们看上去要比\(\mathbb{N}\)大。
可数个至多可数集合的并集是至多可数集合。
证明:
设可数集\(A, B, C,
\cdots\),其元素分别为\(A = \{a_{0},
a_{1}, a_{2}, \cdots\}, B = \{b_{0}, b_{1}, b_{2}, \cdots\},
\cdots\)。将这些元素按照下面的方式排列: \[
\begin{align}
& a_{0} \quad b_{0} \quad c_{0} \quad \cdots \\
& a_{1} \quad b_{1} \quad c_{1} \quad \cdots \\
& a_{2} \quad b_{2} \quad c_{2} \quad \cdots \\
& \ \vdots \quad\ \ \vdots \quad\ \ \ \vdots
\end{align}
\] 然后按对角线与下面的自然数一一对应: \[
\begin{align}
& 0 \quad 2 \quad 5 \quad \cdots \\
& 1 \quad 4 \quad 8 \quad \cdots \\
& 3 \quad 7 \quad 12 \quad \cdots \\
& \vdots \quad\ \vdots \quad\ \vdots
\end{align}
\] 即可得这些集合的并集为可数集。\(\Box\)
无限集合中不是可数集的就是不可数集(uncountable
set)。实数集\(\mathbb{R}\)就是不可数集,证明如下:
\(\mathbb{R}\)的势等于自然数集\(\mathbb{N}\)的幂集的势,即\(|\mathbb{R}| = |\mathcal{P}(\mathbb{N})| =
2^{\aleph_{0}}\)。\(\mathbb{R}\)的势又记作\(\mathfrak{c}\)。
不可数集的势大于可数集,即\(\mathfrak{c} >
\aleph_{0}\)。
针对自然数集的势和实数集的势之间是否还有其它势的问题,德国数学家康托尔(Georg
Cantor,1845—1918)给出了否定的答案,提出了连续统假设(continuum
hypothesis, CH),表述为:
不存在一个集合,其势大于\(\mathbb{N}\)而小于\(\mathbb{R}\)。
假设连续统假设成立,那么\(\mathbb{R}\)的势可以记作\(\aleph_{1}\),读作阿列夫一(aleph-one)。连续统假设等价于以下等式:
\[2^{\aleph_{0}} = \aleph_{1}\]
这个猜想后来被证明独立于我们常用的这个公理系统之外,即不可被证明或证伪。
附:大型运算符
常见的大型运算符有 \[\sum, \prod, \bigcup, \bigcap, \bigvee, \bigwedge\]
给定一些数\(a_{1}, a_{2}, a_{3}, \cdots,
a_{n}\),它们的和\(a_{1} + a_{2} +
a_{3} + \cdots + a_{n}\)可以写作 \[\sum\limits_{i=1}^{n} a_{i}\]
其中下标\(i = 1\)表示\(i\)的初始值为\(1\),上标\(n\)表示\(i\)从初始值\(1\)遍历到\(n\)。上式的意思即\(a_{i}\)的和,\(i\)从\(1\)到\(n\)。
特别注意,如果下标大于上标,式子的值一般定义为\(0\)。
例如, \[\sum\limits_{i=3}^{6} i^{2} = 3^{2} + 4^{2} + 5^{2} + 6^{2} = 86\]
在不造成歧义的情况下,\(\sum\limits_{i=1}^{n}\)可以直接简写成\(\sum\limits\),例如, \[\sum\limits a_{i} = \sum\limits_{i=1}^{n} a_{i}\]
同理,
\(\prod\limits_{i=1}^{n}
a_{i}\)表示\(a_{1}, a_{2}, \cdots,
a_{n}\)的乘积;
\(\bigcap\limits_{i=1}^{n}
A_{i}\)表示集合\(A_{1}, A_{2}, \cdots,
A_{n}\)的交集;
\(\bigvee\limits_{i=1}^{n}
p_{i}\)表示对命题\(p_{1}, p_{2},
\cdots, p_{n}\)取或。
此外,如果我们要限定下标的值,例如下标\(i\)属于非负整数集合\(A\),可以写作 \[\sum\limits_{i \in A} a_{i}\] 如果集合\(A\)可以用描述法写成\(A = \{i | p(i)\}\),那么可以写作 \[\sum\limits_{p(i)} a_{i}\] 如果下标要排除某个数\(m\),可以写作 \[\sum\limits_{i \ne m} a_{i}\]
如果要使用多个大型运算符如\(\sum\limits_{i} \sum\limits_{j}\),可以简写作 \[\sum\limits_{i, j}\]
求和符号比较特殊,它具有线性性: \[ \begin{align} & \sum\limits (a_{i} + b_{i}) = \sum\limits a_{i} + \sum\limits b_{i} \\ & \sum\limits k a_{i} = k \sum\limits a_{i} \end{align} \]
连乘符号也有类似的性质: \[ \begin{align} & \prod\limits a_{i} b_{i} = \prod\limits a_{i} \prod\limits b_{i} \\ & (\prod\limits a_{i})^{k} = \prod\limits a_{i}^{k} \end{align} \]