学习笔记·解析几何

坐标系

极坐标系

在平面内取一点$O$，称为极点（pole）；作一条以它为起点的射线$x$，称为极轴（polar axis）。这样就构成了极坐标系（polar coordinate system）。对极点外任意一点$P$，$|OP|$称为点$P$的极径（radial coordinate），一般用$r$表示；从极轴到射线$OP$的角，称为点$P$的极角（angular coordinate），一般用$\theta$表示。有序实数对$(r, \theta)$就是点$P$的极坐标（polar coordinates）。

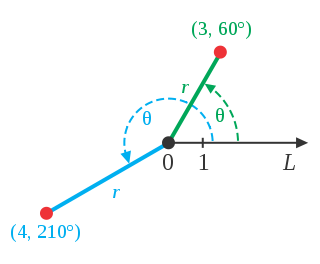
这样，平面内除极点外的任意一点都能用极坐标来表示。对于极坐标为$(r, \theta)$的点，$(r, \theta + 2k \pi) (k \in \mathbb{Z})$也是它的极坐标，也就是说，一个点有无穷多个极坐标。规定$\theta \in [0, 2\pi)$，极点外的每一点才对应唯一的极坐标。极点的极径是$0$，极角没有定义。

通过余弦定理，可以计算得到极坐标系中两点$(r_{1}, \theta_{1}), (r_{2}, \theta_{2})$之间的距离公式：

$$d = \sqrt{r_{1}^{2} + r_{2}^{2} - 2 r_{1} r_{2} \cos(\theta_{1} - \theta_{2})}$$

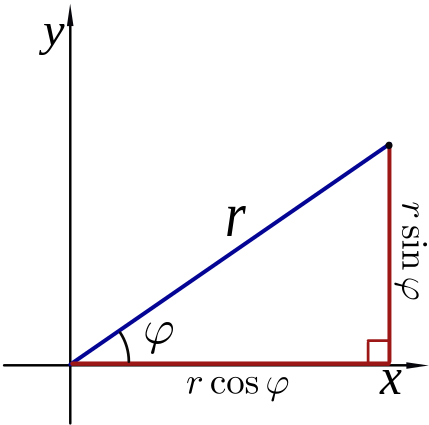
将直角坐标系的原点与极坐标系的极点重合，直角坐标系的$x$非负半轴与极坐标系的极轴重合，设极点外一点$P$的直角坐标和极坐标分别是$(x, y), (r, \theta)$，可以得到

$$\begin{cases} x = r \cos \theta \\ y = r \sin \theta \end{cases}$$

这样就可以将极坐标变换为直角坐标。反过来，如果$\theta \ne k \pi + \dfrac{\pi}{2} (k \in \mathbb{Z})$，也就是$y \ne 0$，那么

$$\begin{cases} r = \sqrt{x^{2} + y^{2}} \\ \tan \theta = \dfrac{y}{x} \end{cases}$$

柱坐标系

如果把空间直角坐标系的坐标平面$Oxy$换成极坐标系，得到的就是柱坐标系（cylindrical coordinate system）。除原点外的任意一点都有柱坐标（cylindrical coordinates）$(r, \theta, z)$。

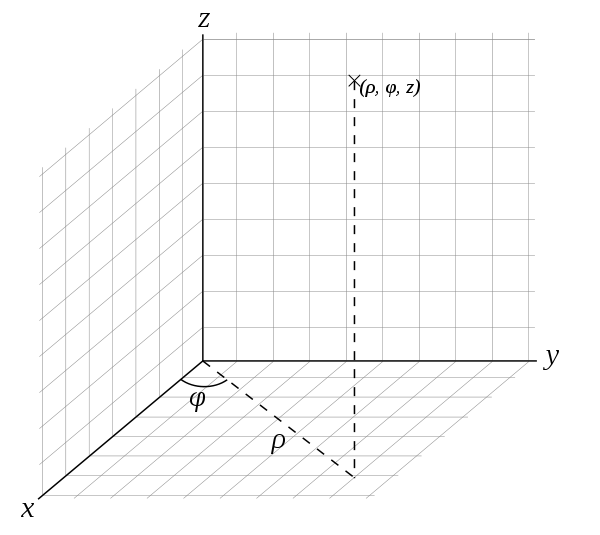
柱坐标与直角坐标的对应关系如下：

$$\begin{cases} x = r \cos \theta \\ y = r \sin \theta \\ z = z \end{cases}$$

球坐标系

在空间直角坐标系内，对原点外任意一点$P$，令$r = |OP|$；$\theta$表示$\overrightarrow{OP}$与$z$轴正方向的夹角，称为天顶角（zenith angle）；设$P$在$Oxy$平面的投影为$Q$，$\varphi$表示从$x$轴逆时针旋转到$OQ$的角，称为方位角（azimuth angle）。这样，点$P$就能用有序实数对$(r, \theta, \varphi)$表示，称为其球坐标（spherical coordinates）。用球坐标来表示的坐标系称为球坐标系（spherical coordinate system）。

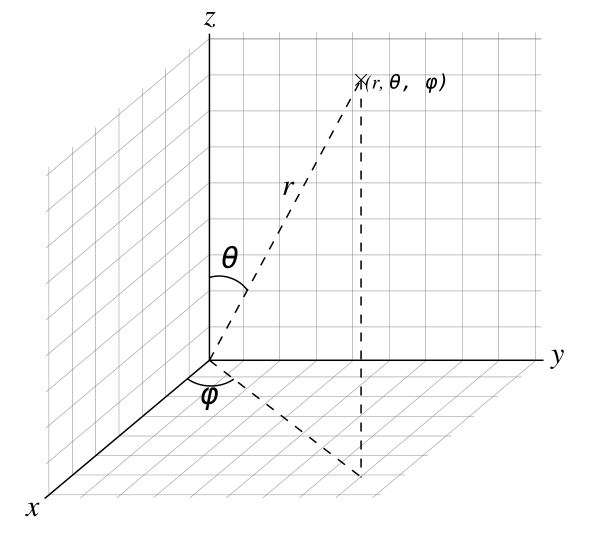
由定义可知，$\theta \in [0, \pi], \varphi \in [0, 2\pi)$。球坐标与直角坐标的对应关系如下：

$$\begin{cases} x = r \sin \theta \cos \varphi \\ y = r \sin \theta \sin \varphi \\ z = r \cos \theta \end{cases}$$

平面解析几何

直线

倾斜角与斜率

在平面直角坐标系内，定义直线与$x$轴所夹的较小的角为倾斜角（angle of inclination），其取值范围就是$[0, \pi)$。如果直线$l$的倾斜角$\alpha \ne \dfrac{\pi}{2}$，令$k = \tan \alpha$，称$k$为直线$l$的斜率（slope）。斜率反映了直线的倾斜程度，斜坡的斜率越大，斜坡也就越陡。

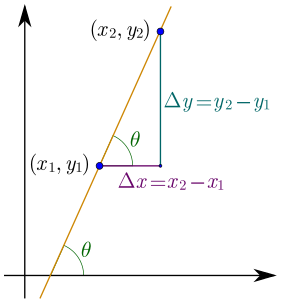
与直线平行的非零向量称为直线的方向向量（direction vector）。设直线$l$的方向向量是$\mathbf{a} = (x, y)$，则满足$\cos \alpha = \dfrac{x}{\sqrt{x^{2} + y^{2}}}, \sin \alpha = \dfrac{y}{\sqrt{x^{2} + y^{2}}}$的角$\alpha \in [0, \pi)$称为直线$l$的倾斜角。如果$\alpha \ne \dfrac{\pi}{2}$，也就是$x \ne 0$，称$k = \tan \alpha = \dfrac{y}{x}$为直线$l$的斜率。这是倾斜角与斜率的另一个定义。

正比例函数$y = kx$的图像是一条直线，根据上面的定义，系数$k$实际上就是它的斜率。对于图像上除原点外任意一点$(x, y)$，满足

$$k = \tan \alpha = \dfrac{y}{x}$$

一般地，设直线$l$斜率为$k$，它与$x, y$轴分别交于$(a, 0), (0, b)$，$a$称为直线$l$在$x$轴上的截距（intercept），$b$称为直线$l$在$y$轴上的截距。直线$l$向下平移$b$个单位，就是经过原点的正比例函数，满足$y - b = kx$，也就是

$$y = kx + b$$

这样，直线$l$就用方程的形式表示出来。这就是直线的斜截式方程（slope–intercept equation）。它实际上等同于一次函数的表达式。如果已知斜率和$x$轴上的截距$a$，那么可以得到类似的方程：

$$y = k (x - a)$$

由斜率的定义可知：
设不重合的两条直线$l_{1}, l_{2}$的斜率分别是$k_{1}, k_{2}$，$l_{1} \parallel l_{2}$当且仅当$k_{1} = k_{2}$。

$l_{1} \perp l_{2}$当且仅当$k_{1} k_{2} = -1$。证明如下：
设$l_{1}, l_{2}$的方向向量分别是$\mathbf{a} = (1, k_{1}), \mathbf{b} = (1, k_{2})$，那么

$$l_{1} \perp l_{2} \Leftrightarrow \mathbf{a} \perp \mathbf{b} \Leftrightarrow \mathbf{a} \cdot \mathbf{b} = 0 \Leftrightarrow 1 + k_{1} k_{2} = 0 \Leftrightarrow k_{1} k_{2} = -1$$

我们还可以用斜率来计算直线之间的夹角。设两条直线$l_{1}, l_{2}$的一个夹角$\alpha \in (0, \dfrac{\pi}{2}) \cup (\dfrac{\pi}{2}, \pi)$，斜率分别为$k_{1}, k_{2}$，有夹角公式：

$$|\tan \alpha| = \left|\dfrac{k_{1} - k_{2}}{1 + k_{1} k_{2}} \right|$$

证明如下：
设$l_{1}, l_{2}$的方向向量分别是$\mathbf{a} = (1, k_{1}), \mathbf{b} = (1, k_{2})$，则$|\cos \alpha| = \dfrac{|\mathbf{a} \cdot \mathbf{b}|}{|\mathbf{a}| |\mathbf{b}|}$；设空间向量$\mathbf{a}’ = (1, k_{1}, 0), \mathbf{b}’ = (1, k_{2}, 0)$，则根据向量积的定义，$\sin \alpha = \dfrac{|\mathbf{a}’ \times \mathbf{b}’|}{|\mathbf{a}’| |\mathbf{b}’|} = \dfrac{|\mathbf{a}’ \times \mathbf{b}’|}{|\mathbf{a}| |\mathbf{b}|}$。两式相除得到$|\tan \alpha| = \dfrac{|\mathbf{a}’ \times \mathbf{b}’|}{|\mathbf{a} \cdot \mathbf{b}|}$。$\mathbf{a}’ \times \mathbf{b}’ = (0, 0, k_{2} - k_{1}), \mathbf{a} \cdot \mathbf{b} = 1 + k_{1} k_{2}$，所以$|\tan \alpha| = \left|\dfrac{k_{1} - k_{2}}{1 + k_{1} k_{2}} \right|$。$\Box$

直线的方程

已知直线$l$的斜率和截距，我们可以用斜截式方程来表示$l$。而在其它的场景下，我们还会用到不同的方程来表示直线。

已知直线$l$上一点$P_{0}(x_{0}, y_{0})$，斜率是$k$：
设$l$上任意一点$P(x, y)$，因为截距不变，利用斜截式，可以得到$y - kx = b = y_{0} - kx_{0}$，整理得

$$y - y_{0} = k (x - x_{0})$$

这就是直线的点斜式方程（point–slope equation）。斜截式方程可以认为是$P_{0}(0, b)$时得点斜式方程。

已知直线$l$上不同的两点$P_{1}(x_{1}, y_{1}), P_{2}(x_{2}, y_{2})$：
首先，如果$x_{1} = x_{2} = x_{0}$，那么直线$l$的方程是$x = x_{0}$，倾斜角是$\dfrac{\pi}{2}$，斜率没有定义。
否则，可以设斜截式为$y = kx + b$，代入点的坐标得到方程组

$$\begin{cases} y_{1} = kx_{1} + b \\ y_{2} = kx_{2} + b \end{cases}$$

两式相减，得到$y_{1} - y_{2} = k (x_{1} - x_{2})$，得到斜率

$$k = \dfrac{y_{1} - y_{2}}{x_{1} - x_{2}}$$

直线$l$经过点$P_{1}$，斜率是$\dfrac{y_{1} - y_{2}}{x_{1} - x_{2}}$，可以用点斜式表示为$y - y_{1} = \dfrac{y_{1} - y_{2}}{x_{1} - x_{2}} (x - x_{1})$，也就是

$$(y - y_{1}) (x_{1} - x_{2}) = (x - x_{1}) (y_{1} - y_{2})$$

这就是直线的两点式方程（two–point equation）。

已知直线$l$在$x, y$轴上的截距分别是$a, b$，且$ab \ne 0$：
直线$l$经过点$A(a, 0), B(0, b)$，由两点式得到$(y - 0) (a - 0) = (x - a) (0 - b)$，也就是

$$\dfrac{x}{a} + \dfrac{y}{b} = 1$$

这就是直线的截距式方程（intercept equation）。

用向量也能得到直线的方程。已知直线$l$的一个法向量$\mathbf{n} = (a, b)$，且经过点$P_{0}(x_{0}, y_{0})$：
对于直线上任意一点$P(x, y)$都有$\overrightarrow{PP_{0}} \cdot \mathbf{n} = 0$，也就是

$$a (x - x_{0}) + b (y - y_{0}) = 0$$

这就是直线的点法式方程（point–normal equation）。

上面表示直线的方程都是一次方程。我们考虑一般的二元一次方程

$$Ax + By + C = 0 (A, B, C \in \mathbb{R}, A^{2} + B^{2} > 0)$$

如果$B = 0$，那么根据条件$A \ne 0$，方程可以化为$x = -\dfrac{C}{A}$，表示一条垂直于$x$轴的直线；
如果$B \ne 0$，那么方程可以化为$y = -\dfrac{A}{B} x - \dfrac{C}{B}$，是点斜式方程。
这样，所有的二元一次方程都表示一条直线。$A^{2} + B^{2} > 0$时，$Ax + By + C = 0$就是直线的一般式方程（general equation）。比较点法式方程可知，直线一定有一个法向量$\mathbf{n} = (A, B)$。

在极坐标系中，如果直线经过极点，那么直线上除极点外任意一点的极角就是$\theta_{0}$或$\pi + \theta_{0}$，其中$\theta_{0} \in [0, \pi)$，直线的极坐标方程就是$\theta = \theta_{0}$或$\pi + \theta_{0} (r \in \mathbb{R})$。为了方便起见，对$\theta \in [0, \pi)$，规定$(r, \theta), (-r, \pi + \theta)$表示同一个点，这样经过极点的直线方程就可以写成

$$\theta = \theta_{0} (r \in \mathbb{R})$$

对于不过极点的直线，设直线经过点$P_{0}(r_{0}, \theta_{0})$，交极轴于点$Q$，极轴到直线的角是$\alpha$，$P(r, \theta)$是直线上任意一点。
图中$\angle OPQ = \alpha - \theta, \angle OP_{0}Q = \alpha - \theta_{0}$，根据正弦定理$\dfrac{r}{\sin(\alpha - \theta_{0})} = \dfrac{r_{0}}{\sin(\alpha - \theta)}$，得到

$$r \sin(\alpha - \theta) = r_{0} \sin(\alpha - \theta_{0})$$

这就是不过极点的直线的极坐标方程。

点到直线、平行直线之间的距离

将直线转化为方程后，就能得到点到直线的距离公式：
点$P(x_{0}, y_{0})$到直线$l: Ax + By + C = 0$的距离

$$d = \dfrac{|Ax_{0} + By_{0} + C|}{\sqrt{A^{2} + B^{2}}}$$

利用向量可以简便地证明：
首先求直线$l$的一个法向量。设$l$上不同的两点$P_{1}(x_{1}, y_{1}), P_{2}(x_{2}, y_{2})$，则$\overrightarrow{P_{1}P_{2}} = (x_{2} - x_{1}, y_{2} - y_{1})$是$l$的方向向量。由直线方程可知

$$\begin{cases} Ax_{1} + By_{1} + C = 0 \\ Ax_{2} + By_{2} + C = 0 \end{cases}$$

两式相减得$A(x_{1} - x_{2}) + B(y_{1} - y_{2}) = 0$，也就是$(A, B) \cdot (x_{2} - x_{1}, y_{2} - y_{1}) = 0$，$\mathbf{n} = (A, B)$是$l$的法向量。
根据投影向量的定义，设$Q(x, y)$是$l$上任意一点，则

$$d = |\operatorname{proj}_{\mathbf{n}} \overrightarrow{PQ}| = \dfrac{|\overrightarrow{PQ} \cdot \mathbf{n}|}{|\mathbf{n}|}$$

$\overrightarrow{PQ} \cdot \mathbf{n} = A (x - x_{0}) + B (y - y_{0}), |\mathbf{n}| = \sqrt{A^{2} + B^{2}}$，由直线方程得$Ax + By = -C$，代入得

$$d = \dfrac{|Ax_{0} + By_{0} + C|}{\sqrt{A^{2} + B^{2}}} \quad \Box$$

两条平行直线之间的距离就是它们的公垂线段的长，实际上可以化为点到直线的距离。设平行直线

$$\begin{align} & l_{1}: Ax + By + C_{1} = 0 \\ & l_{2}: Ax + By + C_{2} = 0 \end{align}$$

任取$l_{2}$上一点$P(x_{0}, y_{0})$，$P$到$l_{1}$的距离就是$l_{1}, l_{2}$之间的距离。由$l_{2}$方程得$Ax_{0} + By_{0} = -C_{2}$，代入点到直线的距离公式，

$$d = \dfrac{|C_{1} - C_{2}|}{\sqrt{A^{2} + B^{2}}}$$

圆

圆的方程

圆是平面内到定点距离等于定长的点的集合。设圆的圆心是点$A(a, b)$，半径是$r$，$P(x, y)$是圆上任意一点，根据这个定义，可以利用两点之间的距离公式建立方程：

$$|PA| = \sqrt{(x - a)^{2} + (y - b)^{2}} = r$$

即

$$(x - a)^{2} + (y - b)^{2} = r^{2}$$

这就是圆的标准方程。

这样，就能用代数方法判定点和圆的位置关系。对于圆$C: (x - a)^{2} + (y - b)^{2} = r^{2}$，点$P(x_{0}, y_{0})$在圆上的充要条件是$(x - a)^{2} + (y - b)^{2} = r^{2}$，在圆内的充要条件是$(x - a)^{2} + (y - b)^{2} < r^{2}$，在圆外的充要条件是$(x - a)^{2} + (y - b)^{2} > r^{2}$。

展开圆的标准方程并整理，可以得到$x^{2} + y^{2} - 2ax - 2by + a^{2} + b^{2} - r^{2} = 0$。令$D = -2a, E = -2b, F = a^{2} + b^{2} - r^{2}$，就得到

$$x^{2} + y^{2} + Dx + Ey + F = 0$$

配方，得到

$$\left(x + \dfrac{D}{2} \right)^{2} + \left(y + \dfrac{E}{2} \right)^{2} = \dfrac{D^{2} + E^{2} - 4F}{4}$$

令$K = D^{2} + E^{2} - 4F$，
如果$K > 0$，比较圆的标准方程，可以看出该方程表示一个以$\left(-\dfrac{D}{2}, -\dfrac{E}{2} \right)$为圆心，$\dfrac{\sqrt{K}}{2}$为半径的圆；
如果$K = 0$，方程表示一个点$\left(-\dfrac{D}{2}, -\dfrac{E}{2} \right)$；
如果$K < 0$，方程没有实数解，不表示任何图形。
$K > 0$时，方程$x^{2} + y^{2} + Dx + Ey + F = 0$称为圆的一般方程。

在极坐标系中，设圆的圆心是点$A(\rho_{0}, \theta_{0})$，半径是$r$，$P(\rho, \theta)$是圆上任意一点，利用极坐标系中两点之间的距离公式可以建立方程：

$$\rho^{2} + \rho_{0}^{2} - 2 \rho \rho_{0} \cos(\theta - \theta_{0}) = r^{2}$$

这就是圆的极坐标方程。

如果圆的圆心是极点，那么令$\rho_{0} = 0$，得到

$$\rho = r$$

如果圆经过极点，那么令$\rho_{0} = r$，得到

$$\rho = 2r \cos(\theta - \theta_{0})$$

直线与圆、圆与圆的位置关系

直线与圆有相交、相切、相离三种位置关系，等价于与圆有2、1、0个交点。将直线和圆都转化为方程后，位置关系的判定就可以转化为方程的解。
联立直线方程与圆的方程，得到一个一元二次方程。设方程是$ax^{2} + bx + c = 0, \Delta = b^{2} - 4ac$，则$\Delta > 0$时，方程有两个解，直线与圆相交；$\Delta = 0$时，方程有一个解，直线与圆相切；$\Delta < 0$时，方程没有实数解，直线与圆相离。

直线与圆的位置关系，也可以通过直线到圆心的距离$d$和圆的半径$r$的大小关系来判定。$0 \le d < r$时，直线与圆相交；$d = r$时，直线与圆相切；$d > r$时，直线与圆相离。

圆与圆之间也有相交、相切、相离三种位置关系，其中相切包括外切和内切，相离包括外离和内含。
设$r_{1}, r_{2}$为两个圆的半径，计算出两个圆连心线的长$d$，则$d > r_{1} + r_{2}$时，两圆外离；$d = r_{1} + r_{2}$时，两圆外切；$|r_{1} - r_{2}| < d < r_{1} + r_{2}$时，两圆相交；$ d = |r_{1} - r_{2}|$时，两圆内切；$0 \le d < |r_{1} - r_{2}|$时，两圆内含。

如果只需要判断相交、相切、相离这三种位置关系，也可以用纯代数的方法。设两个圆的方程

$$\begin{align} & C_{1}: x^{2} + y^{2} + D_{1}x + E_{1}y + F_{1} = 0 \\ & C_{2}: x^{2} + y^{2} + D_{2}x + E_{2}y + F_{2} = 0 \end{align}$$

两式相减，得到

$$(D_{1} - D_{2}) x + (E_{1} - E_{2}) y + F_{1} - F_{2} = 0$$

如果$D_{1} = D_{2}, E_{1} = E_{2}$，两圆圆心相同，半径不同，显然是内含关系；否则，该方程就表示一条直线，这条直线称为两个圆的根轴（radical axis）。

由根轴定义可知：
一个点是两个圆的交点的充要条件是它在其中一个圆和两个圆的根轴上。
证明：
设圆$C_{1}, C_{2}$的方程分别是$f_{1}(x, y) = 0, f_{2}(x, y) = 0$，则根轴方程是

$$f_{1}(x, y) - f_{2}(x, y) = 0$$

必要性：设$P(x_{0}, y_{0})$在圆$C_{1}, C_{2}$上，那么$f_{1}(x_{0}, y_{0}) = 0, f_{2}(x_{0}, y_{0}) = 0$，这样$f_{1}(x_{0}, y_{0}) - f_{2}(x_{0}, y_{0}) = 0$；
充分性：设$P(x_{0}, y_{0})$在圆$C_{2}$和根轴上，则$f_{1}(x_{0}, y_{0}) = f_{2}(x_{0}, y_{0}) + (f_{1}(x_{0}, y_{0}) - f_{2}(x_{0}, y_{0})) = 0$，也在圆$C_{1}$上。$\Box$

对于两个相交的圆，既然两个交点都在根轴上，那么两点确定一条直线。两个圆的公共弦所在直线就是根轴。

两个圆的公共点个数与它们的根轴和其中一个圆的交点个数是相同的，圆与圆的位置关系判定问题就可以转化为直线与圆的位置关系判定问题。

曲线

一般的平面曲线（curve）是指平面上的点集，在平面直角坐标系中可以表示成下面的形式：

$$C = \{(x, y) | f(x, y) = 0\}$$

点$P \in C$即点$P$在曲线$C$上的充要条件是$f(x, y) = 0$，$f(x, y) = 0$就是曲线$C$的方程。

平面上的动点$S(x, y)$满足条件$P$，它在平面上运动得到的曲线可以表示为

$$\{S | P(S)\}$$

如果$P(S)$等价于$f(x, y) = 0$，则$f(x, y) = 0$称为动点$S$的轨迹方程（locus equation），曲线称为动点$S$的轨迹（locus）。

有时候，曲线不是用$f(x, y) = 0$的形式来表示的。点$P(x, y)$在曲线$C$上等价于存在实数$t$使得

$$\begin{cases} x = g(t) \\ y = h(t) \end{cases}$$

其中$g, h$是两个函数。这就是曲线$C$的参数方程（parametric equation），$t$称为参数（parameter）。

设一个圆的圆心是$(a, b)$，半径是$r$，其标准方程就是$(x - a)^{2} + (y - b)^{2} = r^{2}$。这样就有$|x - a|, |y - b| \le r$。令$x - a = r \cos \theta (\theta \in [0, 2\pi])$，代入可得$y - b = \pm r \sin \theta$，不妨取正号，得到

$$\begin{cases} x = a + r \cos \theta \\ y = b + r \sin \theta \end{cases}$$

这就是圆的参数方程。参数$\theta$的几何意义就是从$(a, b + r)$出发的动点逆时针转过的角度。

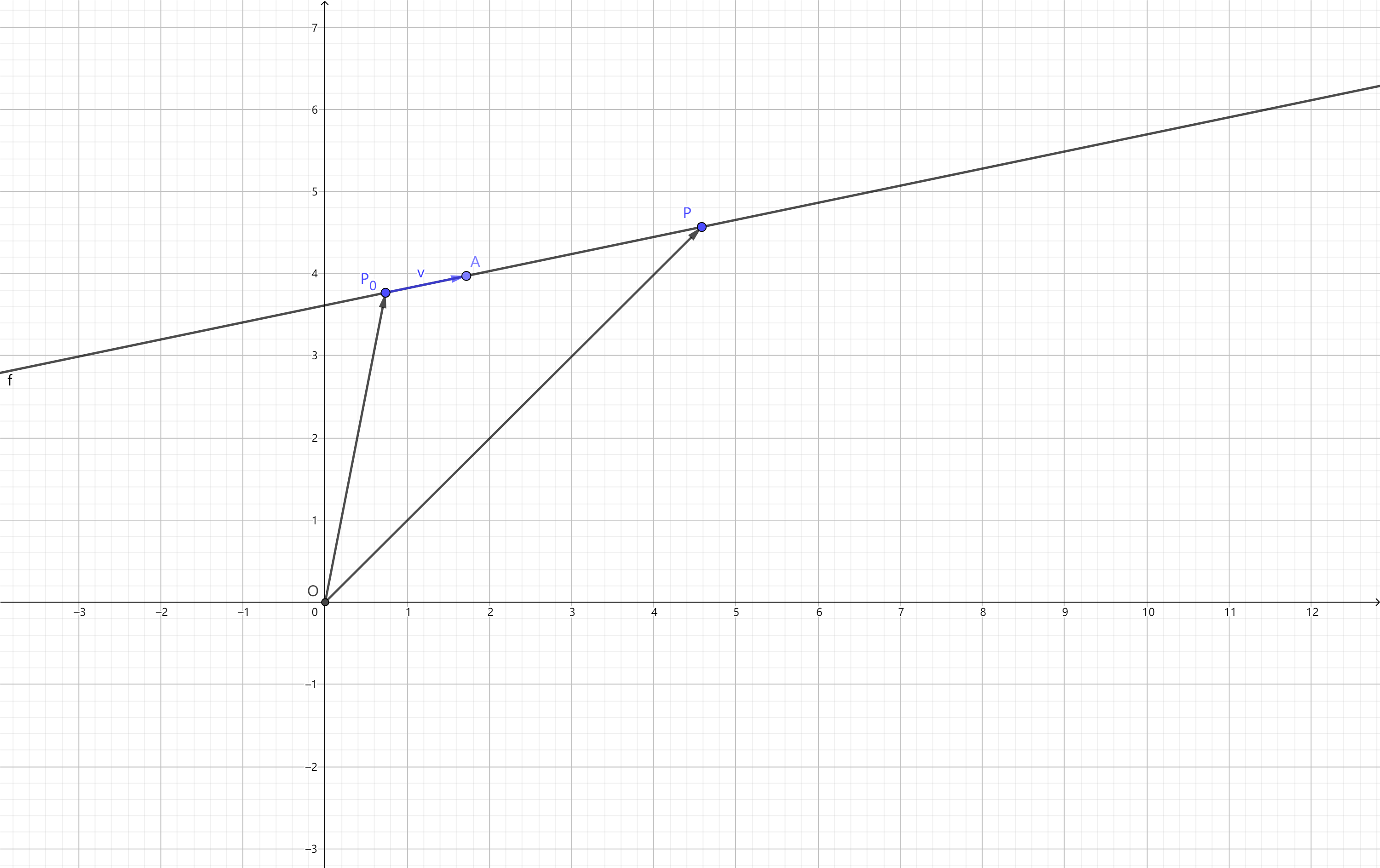
设一条直线的倾斜角是$\theta$，经过点$P_{0}(x_{0}, y_{0})$。取单位方向向量$\mathbf{u} = (\cos \theta, \sin \theta)$，任取直线上一点$P(x, y)$，则存在实数$t$使得$\overrightarrow{OP} = \overrightarrow{OP_{0}} + t \mathbf{u}$。用坐标形式表示，就是

$$\begin{cases} x = x_{0} + t \cos \theta \\ y = y_{0} + t \sin \theta \end{cases}$$

这就是直线的参数方程。参数$t$的几何意义就是$P_{0}, P$之间的距离，其正负由$\mathbf{u}$的方向决定。

空间解析几何

空间平面与空间直线

平面的方程

在空间直角坐标系中，设平面$\alpha$的一个法向量$\mathbf{n} = (a, b, c)$，且经过点$P_{0}(x_{0}, y_{0}, z_{0})$，则对平面内任意一点$P(x, y, z)$都有$\overrightarrow{PP_{0}} \cdot \mathbf{n} = 0$，也就是

$$a (x - x_{0}) + b (y - y_{0}) + c (z - z_{0}) = 0$$

这就是平面的点法式方程（point–normal equation）。

一般地，三元一次方程

$$Ax + By + Cz + D = 0 (A, B, C, D \in \mathbb{R}, A^{2} + B^{2} + C^{2} > 0)$$

总是表示一个平面。这样的方程就称为平面的一般式方程（general equation）。比较点法式方程可知，平面一定有一个法向量$\mathbf{n} = (A, B, C)$。

此外，设平面$\alpha$经过点$P_{0}(x_{0}, y_{0}, z_{0})$，且与两个不共线的向量$\mathbf{u} = (a_{1}, b_{1}, c_{1}), \mathbf{v} = (a_{2}, b_{2}, c_{2})$都平行。根据共面向量定理，对平面内任意一点$P(x, y, z)$都有$\overrightarrow{PP_{0}} = s \mathbf{u} + t \mathbf(v) (s, t \in \mathbb{R})$，代入得

$$\begin{cases} x = x_{0} + sa_{1} + ta_{2} \\ y = y_{0} + sb_{1} + tb_{2} \\ z = z_{0} + sc_{1} + tc_{2} \end{cases}$$

方程含有$s, t$两个参数，因此称为平面的参数方程。由$\overrightarrow{PP_{0}} \cdot (\mathbf{u} \times \mathbf{v}) = 0$，也能得到平面的点法式方程。

设平面$\alpha$与$x, y, z$轴分别交于点$P_{1}(a, 0, 0), P_{2}(0, b, 0), P_{3}(0, 0, c)$，其中$abc \ne 0$。利用上面的结论，设$\mathbf{u} = \overrightarrow{P_{1}P_{2}} = (-a, b, 0), \mathbf{v} = \overrightarrow{P_{1}P_{3}} = (-a, 0, c)$，则$\mathbf{u} \times \mathbf{v} = (bc, ac, ab)$。对平面内任意一点$P(x, y)$都有$\overrightarrow{PP_{1}} \cdot (\mathbf{u} \times \mathbf{v}) = 0$，得到$(x - a) bc + yac + zab = 0$，也就是

$$\dfrac{x}{a} + \dfrac{y}{b} + \dfrac{z}{c} = 1$$

这就是平面的截距式方程（intercept equation）。

直线的方程

设空间直角坐标系中一条直线的方向向量$\mathbf{u} = (a, b, c)$，且经过点$P_{0}(x_{0}, y_{0}, z_{0})$。对于直线上任意一点$P(x, y, z)$，$\overrightarrow{PP_{0}} = t \mathbf{u} (t \in \mathbb{R})$，得到

$$\begin{cases} x = x_{0} + ta \\ y = y_{0} + tb \\ z = z_{0} + tc \end{cases}$$

这就是直线的参数方程。消去参数$t$，可以得到

$$\dfrac{x - x_{0}}{a} = \dfrac{y - y_{0}}{b} = \dfrac{z - z_{0}}{c}$$

这就是直线的标准方程。

此外，也可以把直线看成两个平面的交线，用三元一次方程组表示为

$$\begin{cases} A_{1}x + B_{1}y + C_{1}z + D_{1} = 0 \\ A_{2}x + B_{2}y + C_{2}z + D_{2} = 0 \end{cases}$$

这就是直线的一般方程。

平面与直线的位置关系

平面与平面的位置关系

设两个平面$\pi_{1}, \pi_{2}$，$\pi_{i}$的一般式方程是$A_{i}x + B_{i}y + C_{i}z + D_{i} = 0$，显然：
$\pi_{1} \parallel \pi_{2}$的充要条件是$\dfrac{A_{1}}{A_{2}} = \dfrac{B_{1}}{B_{2}} = \dfrac{C_{1}}{C_{2}} \ne \dfrac{D_{1}}{D_{2}}$;
$\pi_{1} \perp \pi_{2}$的充要条件是$A_{1}A_{2} + B_{1}B_{2} + C_{1}C_{2} = 0$。

设三个平面$\pi_{1}, \pi_{2}, \pi_{3}$两两不平行，$\pi_{i}$的法向量是$\mathbf{n}_{i}$，则三个平面有唯一交点的充要条件是$(\mathbf{n}_{1}, \mathbf{n}_{2}, \mathbf{n}_{3}) \ne 0$。
证明：
必要性：$\mathbf{n}_{1} \times \mathbf{n}_{2}, \mathbf{n}_{2} \times \mathbf{n}_{3}, \mathbf{n}_{3} \times \mathbf{n}_{1}$三个向量不共面，因此$(\mathbf{n}_{1} \times \mathbf{n}_{2}, \mathbf{n}_{2} \times \mathbf{n}_{3}, \mathbf{n}_{3} \times \mathbf{n}_{1}) \ne 0$。根据拉格朗日恒等式：

$$\begin{align} (\mathbf{n}_{1} \times \mathbf{n}_{2}, \mathbf{n}_{2} \times \mathbf{n}_{3}, \mathbf{n}_{3} \times \mathbf{n}_{1}) &= ((\mathbf{n}_{1} \times \mathbf{n}_{2}) \times (\mathbf{n}_{2} \times \mathbf{n}_{3})) \cdot (\mathbf{n}_{3} \times \mathbf{n}_{1}) \\ &= ((\mathbf{n}_{1} \cdot (\mathbf{n}_{2} \times \mathbf{n}_{3})) \mathbf{n}_{2} - (\mathbf{n}_{2} \cdot (\mathbf{n}_{2} \times \mathbf{n}_{3})) \mathbf{n}_{1}) \cdot (\mathbf{n}_{3} \times \mathbf{n}_{1}) \\ &= ((\mathbf{n}_{1}, \mathbf{n}_{2}, \mathbf{n}_{3}) \mathbf{n}_{2} - (\mathbf{n}_{2}, \mathbf{n}_{2}, \mathbf{n}_{3}) \mathbf{n}_{1}) \cdot (\mathbf{n}_{3} \times \mathbf{n}_{1}) \\ &= (\mathbf{n}_{1}, \mathbf{n}_{2}, \mathbf{n}_{3}) \mathbf{n}_{2} \cdot (\mathbf{n}_{3} \times \mathbf{n}_{1}) \\ &= (\mathbf{n}_{1}, \mathbf{n}_{2}, \mathbf{n}_{3})^{2} \end{align}$$

所以$(\mathbf{n}_{1}, \mathbf{n}_{2}, \mathbf{n}_{3}) \ne 0$。
充分性：同上，如果$(\mathbf{n}_{1}, \mathbf{n}_{2}, \mathbf{n}_{3}) \ne 0$，那么$(\mathbf{n}_{1} \times \mathbf{n}_{2}, \mathbf{n}_{2} \times \mathbf{n}_{3}, \mathbf{n}_{3} \times \mathbf{n}_{1}) \ne 0$。设$l_{ij} = \pi_{i} \cap \pi_{j}$，此时$l_{12}, l_{23}, l_{31}$没有平行或重合的。设$P = l_{12} \cap l_{23}$，则$P \in \pi_{1} \cap \pi_{2} \cap \pi_{3}$，从而$P \in l_{23}$，故$P$是$\pi_{1}, \pi_{2}, \pi_{3}$的唯一交点。$\Box$

平面与直线的位置关系

设平面$\pi$的方程是$Ax + By + Cz + D = 0$，直线$l$的标准方程是$\dfrac{x - x_{0}}{X} = \dfrac{y - y_{0}}{Y} = \dfrac{z - z_{0}}{Z}$，那么：
$l \parallel \pi$的充要条件是$AX + BY + CZ = 0, Ax_{0} + By_{0} + Cz_{0} + D \ne 0$；
$l \subset \pi$的充要条件是$AX + BY + CZ = 0, Ax_{0} + By_{0} + Cz_{0} + D = 0$；
$l \perp \pi$的充要条件是$\dfrac{A}{X} = \dfrac{B}{Y} = \dfrac{C}{Z}$。

设平面$\pi$的法向量是$\mathbf{n} = (A, B, C)$，考虑直线$l$的一般方程

$$\begin{cases} A_{1}x + B_{1}y + C_{1}z + D_{1} = 0 \\ A_{2}x + B_{2}y + C_{2}z + D_{2} = 0 \end{cases}$$

其中$\mathbf{n}_{1} = (A_{1}, B_{1}, C_{1}), \mathbf{n}_{2} = (A_{2}, B_{2}, C_{2})$，则$l, \pi$交于一点的充要条件是$(\mathbf{n}_{1}, \mathbf{n}_{2}, \mathbf{n}) \ne 0$。

再用标准方程讨论$l \parallel \pi, l \subset \pi$两种情况。$(\mathbf{n}_{1}, \mathbf{n}_{2}, \mathbf{n}) = 0$，则$\mathbf{n}_{1}, \mathbf{n}_{2}, \mathbf{n}$共面。设$\mathbf{n} = \lambda \mathbf{n}_{1} + \mu \mathbf{n}_{2}$，则$A = \lambda A_{1} + \mu A_{2}, B = \lambda B_{1} + \mu B_{2}, C = \lambda C_{1} + \mu C_{2}$，进一步得到：
$l \subset \pi$的充要条件是存在不全为零的实数$\lambda, \mu$使得$(A, B, C, D) = \lambda (A_{1}, B_{1}, C_{1}, D_{1}) + \mu (A_{2}, B_{2}, C_{2}, D_{2})$。

这告诉我们，设直线$l = \pi_{1} \cap \pi_{2}$，平面$\pi_{i}$的方程是$f_{i} = 0$，则所有经过直线$l$的平面都可以表示为

$$\lambda f_{1} + \mu f_{2} = 0$$

这些平面称为以$l$为轴的共轴平面系。

直线与直线的位置关系

设直线$l_{1}, l_{2}$分别经过两个不同的点$P_{1}, P_{2}$，方向向量分别是$\mathbf{u}_{1}, \mathbf{u}_{2}$，设$\mathbf{u} = \overrightarrow{P_{1}P_{2}}$，则：
$l_{1}, l_{2}$共面的充要条件是$(\mathbf{u}, \mathbf{u}_{1}, \mathbf{u}_{2}) = 0$；
$l_{1} \parallel l_{2}$的充要条件是$\mathbf{u}_{1} \parallel \mathbf{u}_{2}$；
$l_{1} \perp l_{2}$的充要条件是$\mathbf{u}_{1} \perp \mathbf{u}_{2}$；
$l_{1}, l_{2}$重合的充要条件是$\mathbf{u}, \mathbf{u}_{1}, \mathbf{u}_{2}$共线。

解析表示与空间向量的应用

距离

与平面解析几何类似，点$P(x_{0}, y_{0}, z_{0})$到平面$\pi: Ax + By + Cz + D = 0$的距离公式是：

$$d = \dfrac{|Ax_{0} + By_{0} + Cz_{0} + D|}{\sqrt{A^{2} + B^{2} + C^{2}}}$$

类似地，两个平行平面的距离就是

$$d = \dfrac{|D_{1} - D_{2}|}{\sqrt{A^{2} + B^{2} + C^{2}}}$$

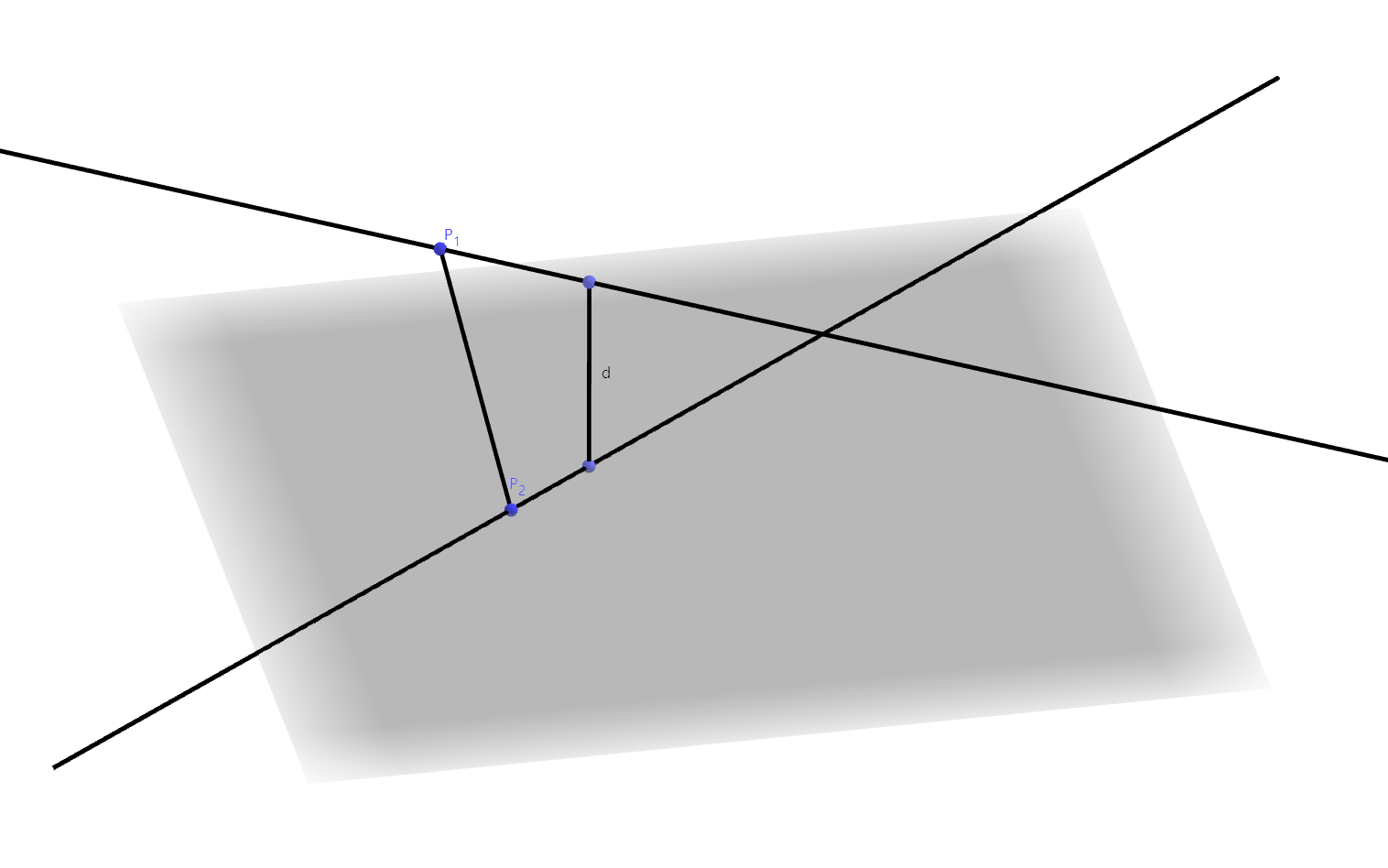两条异面直线的公垂线是指与两条直线均垂直相交的直线，两条异面直线的距离就是其公垂线上两个垂足之间的距离。
设两条异面直线$l_{1}, l_{2}$分别经过点$P_{1}, P_{2}$，方向向量是$\mathbf{u}_{1}, \mathbf{u}_{2}$。过$l_{2}$作平面$\pi \parallel l_{1}$，则$\pi$的法向量是$\mathbf{n} = \mathbf{u}_{1} \times \mathbf{u}_{2}$。两条直线的距离就是$P_{1}$到$\pi$的距离：

$$d = \dfrac{|(\mathbf{u}_{1} \times \mathbf{u}_{1}) \cdot \overrightarrow{P_{1}P_{2}}|}{|\mathbf{u}_{1} \times \mathbf{u}_{1}|} = \dfrac{|(\mathbf{u}_{1}, \mathbf{u}_{2}, \overrightarrow{P_{1}P_{2}})|}{|\mathbf{u}_{1} \times \mathbf{u}_{1}|}$$

点到直线的距离依然可以利用直线的方向向量求得。设直线$l$经过点$P_{0}$，方向向量是$\mathbf{u}$，则点$P$到直线$l$的距离就是向量$\overrightarrow{P_{0}P}$在$\mathbf{u}$上的外投影长度：

$$d = \dfrac{|\mathbf{u} \times \overrightarrow{P_{0}P}|}{|\mathbf{u}|}$$

夹角

设两条直线的方向向量分别是$\mathbf{u}_{1}, \mathbf{u}_{2}$，则较小的夹角

$$\theta = \arccos |\cos \langle \mathbf{u}_{1}, \mathbf{u}_{2} \rangle| = \arccos \dfrac{|\mathbf{u}_{1} \cdot \mathbf{u}_{2}|}{|\mathbf{u}_{1}||\mathbf{u}_{2}|}$$

直线与平面的夹角也就是直线与其在平面上射影的夹角。设直线的方向向量是$\mathbf{u}$，平面的法向量是$\mathbf{n}$，则

$$\theta = \arccos |\sin \langle \mathbf{u}, \mathbf{n} \rangle| = \arccos \dfrac{|\mathbf{u} \times \mathbf{n}|}{|\mathbf{u}||\mathbf{n}|}$$

设两个半平面的法向量分别是$\mathbf{n}_{1}, \mathbf{n}_{2}$，$\theta_{0} = \langle \mathbf{n}_{1}, \mathbf{n}_{2} \rangle = \arccos \dfrac{\mathbf{n}_{1} \cdot \mathbf{n}_{2}}{|\mathbf{n}_{1}||\mathbf{n}_{2}|}$，则二面角$\theta = \theta_{0}$或$\theta = \pi - \theta_{0}$。
实际上，为了确定取值，可以按以下方法计算二面角：
设二面角$A-BC-D$，$\mathbf{n}_{1} = \overrightarrow{BA} \times \overrightarrow{BC}, \mathbf{n}_{2} = \overrightarrow{BD} \times \overrightarrow{BC}$，则二面角

$$\theta = \langle \mathbf{n}_{1}, \mathbf{n}_{2} \rangle = \arccos \dfrac{\mathbf{n}_{1} \cdot \mathbf{n}_{2}}{|\mathbf{n}_{1}||\mathbf{n}_{2}|}$$

基本空间曲面

一般的曲面（surface）是指空间上的点集。如果点$P(x, y, z)$在曲面$S$上的充要条件是满足方程$F(x, y, z) = 0$，那么称$F(x, y, z) = 0$为曲面$S$的方程。
曲面的参数方程一般含有两个参数，也就是

$$\begin{cases} x = f(u, v) \\ y = g(u, v) \\ z = h(u, v) \end{cases}$$

那么，曲面就可以看成是从二维空间$\mathbb{R}^{2}$到三维空间$\mathbb{R}^{3}$的映射。

类似地，三维空间中的曲线就是$\mathbb{R}$到$\mathbb{R}^{3}$的映射，可以表示成参数方程

$$\begin{cases} x = f(t) \\ y = g(t) \\ z = h(t) \end{cases}$$

曲线有时候也可以表示成两个曲面的交线，写成

$$\begin{cases} F(x, y, z) = 0 \\ G(x, y, z) = 0 \end{cases}$$

旋转面

旋转面（surface of revolution）是空间曲线绕一条直线旋转一周形成的曲面。这条直线称为旋转面的轴线（axis），曲线称为旋转面的母线（generatrix）。母线上的一点经过旋转形成的圆称为旋转面的纬圆。以轴线为界的半平面与旋转面的交线是母线，称为旋转面的经线（meridian）。

已知曲线$\gamma$的方程和轴线$l$的方程，可以通过定义来求出旋转面$S$的方程。设空间中一点$P \in S$，也就是说，$P$由$\gamma$上某个点$P_{0}$旋转而来，存在一点$P_{0}$使其对应的纬圆经过点$P$。设直线$l$的方向向量是$\mathbf{u}$，则$\overrightarrow{PP_{0}} \cdot \mathbf{u} = 0$，且$P, P_{0}$到$l$距离相等。设$Q$为直线$l$上一点，则$|PQ| = |P_{0}Q|$，得到方程

$$\begin{cases} \overrightarrow{PP_{0}} \cdot \mathbf{u} = 0 \\ |PQ| = |P_{0}Q| \end{cases}$$

对于一些特殊情况，可以直接求出旋转面的方程。设平面$Oyz$内的曲线$\gamma$方程是$\begin{cases} f(y, z) = 0 \\ x = 0 \end{cases}$，则$\gamma$绕$z$轴旋转得到的曲面方程是

$$f(\sqrt{x^{2} + y^{2}}, z) \cdot f(-\sqrt{x^{2} + y^{2}}, z) = 0$$

以直线为母线的旋转面

有一些旋转面以直线为母线。根据母线与轴线的位置关系，有四种不同的情况。

母线与轴线垂直时，旋转面为平面。如果垂直相交，则是完整的平面；如果垂直异面，则是平面的子集。

母线与轴线平行时，旋转面为圆柱面（cylindrical surface）。圆柱面上的点到轴线的距离称为半径（radius）。
设圆柱面$S$的轴线$l$经过点$P_{0}$且方向向量是$\mathbf{u}$，半径是$r$，则根据点到直线的距离公式，点$P \in S$当且仅当$\dfrac{|\overrightarrow{P_{0}P} \times \mathbf{u}|}{|\mathbf{u}|} = r$。圆柱面的向量式方程（vector equation）就是

$$|\overrightarrow{P_{0}P} \times \mathbf{u}| = r |\mathbf{u}|$$

如果已知圆柱面上一点$Q$，则方程还可以表示为

$$|\overrightarrow{P_{0}P} \times \mathbf{u}| = |\overrightarrow{P_{0}Q} \times \mathbf{u}|$$

母线与轴线相交但不垂直时，旋转面为圆锥面（circular conical surface）。母线与轴线的交点称为顶点（apex），夹角称为半顶角。
设圆锥面$S$的顶点是$P_{0}$，半顶角是$\alpha$，轴线的方向向量是$\mathbf{u}$，则点$P \in S$当且仅当$P_{0}P$与轴线的夹角是$\alpha$，得到圆锥面的向量式方程：

$$|\overrightarrow{P_{0}P} \cdot \mathbf{u}| = |\overrightarrow{P_{0}P}||\mathbf{u}| \cos \alpha$$

如果已知圆柱面上一点$Q$，则$\dfrac{|\overrightarrow{P_{0}P} \cdot \mathbf{u}|}{|\overrightarrow{P_{0}P}||\mathbf{u}|} = \cos \alpha = \dfrac{|\overrightarrow{P_{0}Q} \cdot \mathbf{u}|}{|\overrightarrow{P_{0}Q}||\mathbf{u}|}$，即

$$|\overrightarrow{P_{0}P} \cdot \mathbf{u}||\overrightarrow{P_{0}Q}| = |\overrightarrow{P_{0}Q} \cdot \mathbf{u}||\overrightarrow{P_{0}P}|$$

母线与轴线异面且不垂直时，旋转面为单叶双曲面（one-sheet hyperboloid），这里不多讨论。

柱面与锥面

柱面

考虑空间曲线$\gamma$和非零向量$\mathbf{u}$。对于$\gamma$上每一点，都过该点作与$\mathbf{u}$平行的直线。这些直线的并集形成一个曲面，称为柱面（general cylindrical surface）。这些直线称为柱面的直母线，曲线$\gamma$及其平移得到的曲线称为柱面的准线（directrix），$\mathbf{u}$称为柱面的方向。圆柱面就是以圆为准线的柱面。
平面是一种特殊的柱面，任何非零向量都可以作为其方向。除此以外，柱面方向唯一，我们说柱面平行于$\mathbf{u}$。

设柱面$S$平行于$\mathbf{u}$，准线是$\gamma$，则点$P \in S$当且仅当$P$在$S$的直母线上，也就是说，存在点$P_{0} \in \gamma$和实数$t$使得$\overrightarrow{P_{0}P} = t \mathbf{u}$，即：
设$\mathbf{u} = (k, m, n)$，准线$\gamma: \begin{cases} F(x, y, z) = 0 \\ G(x, y, z) = 0 \end{cases}$，则$P(x, y, z) \in S$的充要条件是：存在实数$t$使得

$$\begin{cases} F(x + tk, y + tm, z + tn) = 0 \\ G(x + tk, y + tm, z + tn) = 0 \end{cases}$$

我们通常要消去$t$，得到曲面的一般方程。有时，柱面的准线是平面曲线，即曲线上各点共面，方程表示为

$$\begin{cases} Ax + By + Cz + D = 0 \\ F(x, y, z) = 0 \end{cases}$$

如果$Ak + Bm + Cn \ne 0$，则柱面的方程是

$$F(x - x_{0}, y - y_{0}, z - z_{0}) = 0$$

其中

$$\begin{cases} x_{0} = \dfrac{k (Ax + By + Cz + D)}{Ak + Bm + Cn} \\ y_{0} = \dfrac{m (Ax + By + Cz + D)}{Ak + Bm + Cn} \\ z_{0} = \dfrac{n (Ax + By + Cz + D)}{Ak + Bm + Cn} \end{cases}$$

如果柱面的准线在平面$Oxy$内，方程是$\begin{cases} f(x, y) = 0 \\ z = 0 \end{cases}$，柱面平行于$\mathbf{u} = (k, m, n) (n \ne 0)$，可以更简便地得到柱面方程为$f(x - \dfrac{k}{n} z, y - \dfrac{m}{n} z)$；
如果柱面的准线在平面$Oxy$内，方程是$\begin{cases} f(x, y) = 0 \\ z = 0 \end{cases}$，柱面平行于$z$轴，则柱面方程为$f(x, y) = 0$。

锥面

考虑空间曲线$\gamma$和$\gamma$外一点$P_{0}$。对于$\gamma$上每一点，都与$P_{0}$相连，得到直线的并集形成一个曲面，称为锥面（conical surface）。$P_{0}$称为锥面的顶点，这些直线称为锥面的直母线，$\gamma$及其位似像称为锥面的准线。圆锥面就是以圆为准线的锥面。

设锥面$S$的顶点是$P_{0}$，准线是$\gamma$，则顶点外一点$P \in S$当且仅当存在点$P’ \in \gamma$使得$P, P’, P_{0}$三点共线，也就是$\overrightarrow{OP’} = t \overrightarrow{OP} + (1 - t) \overrightarrow{OP_{0}}$，于是：
设$P_{0}(x_{0}, y_{0}, z_{0})$，准线$\gamma: \begin{cases} F(x, y, z) = 0 \\ G(x, y, z) = 0 \end{cases}$，则$P(x, y, z) \in S$的充要条件是：存在实数$t$使得

$$\begin{cases} F(tx + (1 - t) x_{0}, ty + (1 - t) y_{0}, tz + (1 - t) z_{0}) = 0 \\ G(tx + (1 - t) x_{0}, ty + (1 - t) y_{0}, tz + (1 - t) z_{0}) = 0 \end{cases}$$