关于三角形的一些几何证明

发表于 分类于 阅读次数： Disqus： 本文字数： 1.3k 阅读时长 ≈ 5 分钟

这好像是全博客第一篇与文化课有点关系的……
（rgq：真好玩）

正弦定理

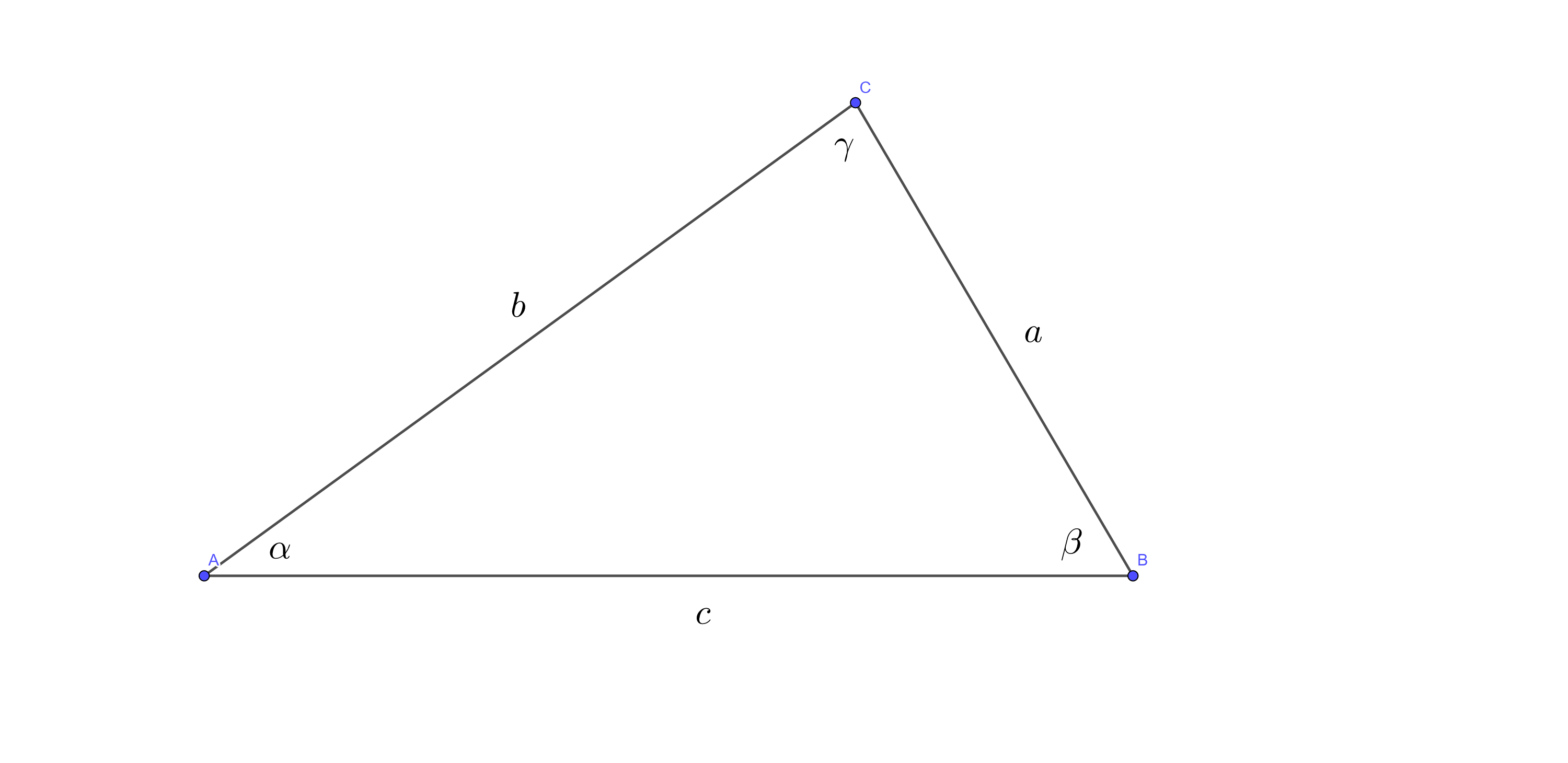
如图，在\(\triangle ABC\)中，\(BC = a, AC = b, AB = c\)，\(r\)为\(\triangle ABC\)的外接圆半径，正弦定理有： \[\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2r\]

证明如下：

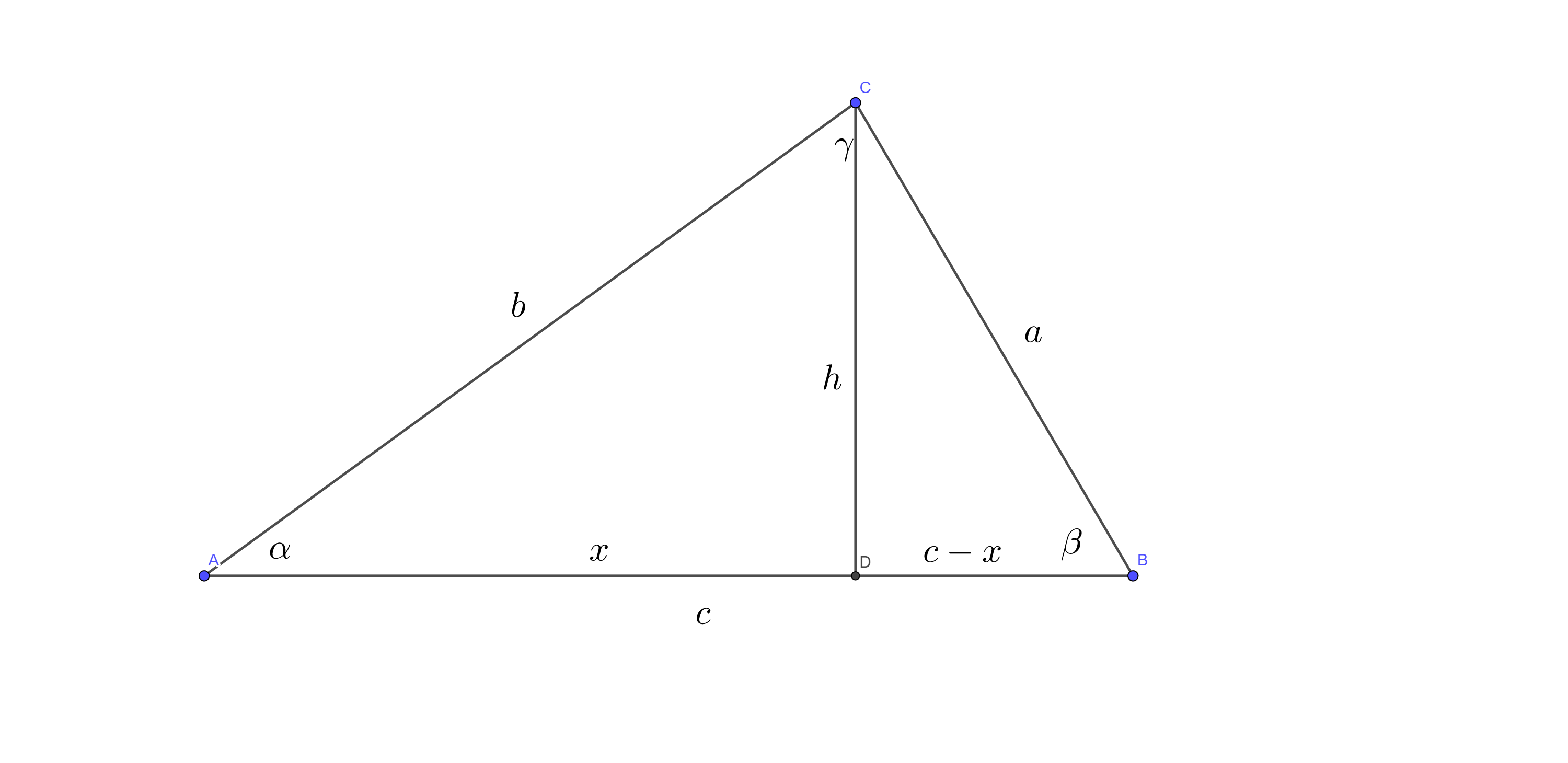如图，过点\(C\)作\(CD \perp AB\)交\(AB\)于点\(D\)，\(CD = h\)。

\[ \begin{align} \because \ & \sin A = \dfrac{h}{b}, \sin B = \dfrac{h}{a} \\ \therefore \ & h = b \sin A = a \sin B \\ \therefore \ & \dfrac{a}{\sin A} = \dfrac{b}{\sin B} \end{align} \] 同理： \[\dfrac{b}{\sin B} = \dfrac{c}{\sin C}\]

作\(\triangle ABC\)的外接圆，设半径为\(r\)。

  • \(\angle A\)为锐角时

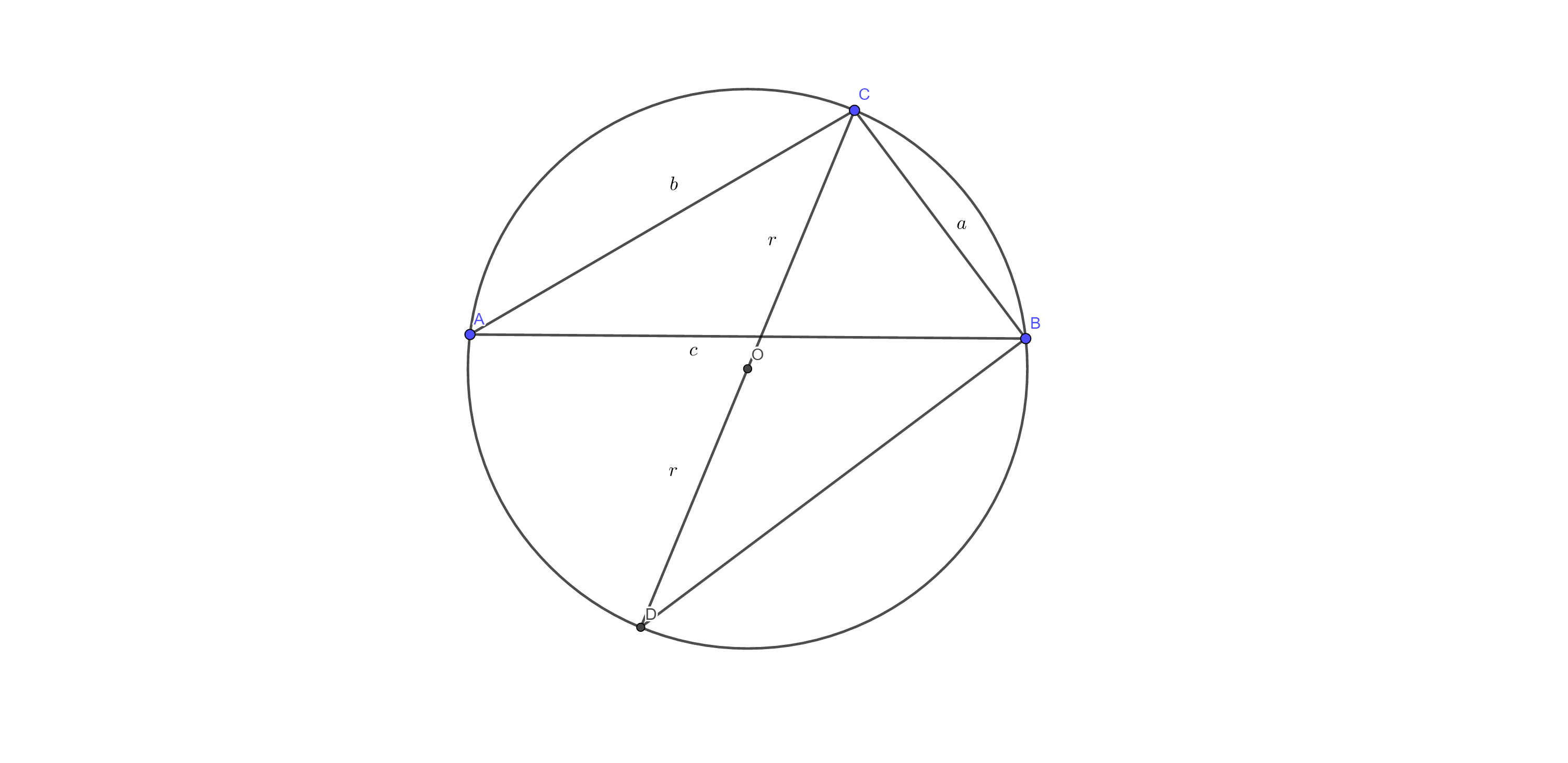
根据圆周角定理，\(\angle D = \angle A\)。 由于\(CD\)为外接圆直径，\(\angle CBD = \dfrac{\pi}{2}\)。 \[ \begin{align} \therefore \ & \sin A = \sin D = \dfrac{a}{2r} \\ \therefore \ & \dfrac{a}{\sin A} = 2r \end{align} \]

  • \(\angle A\)为直角时

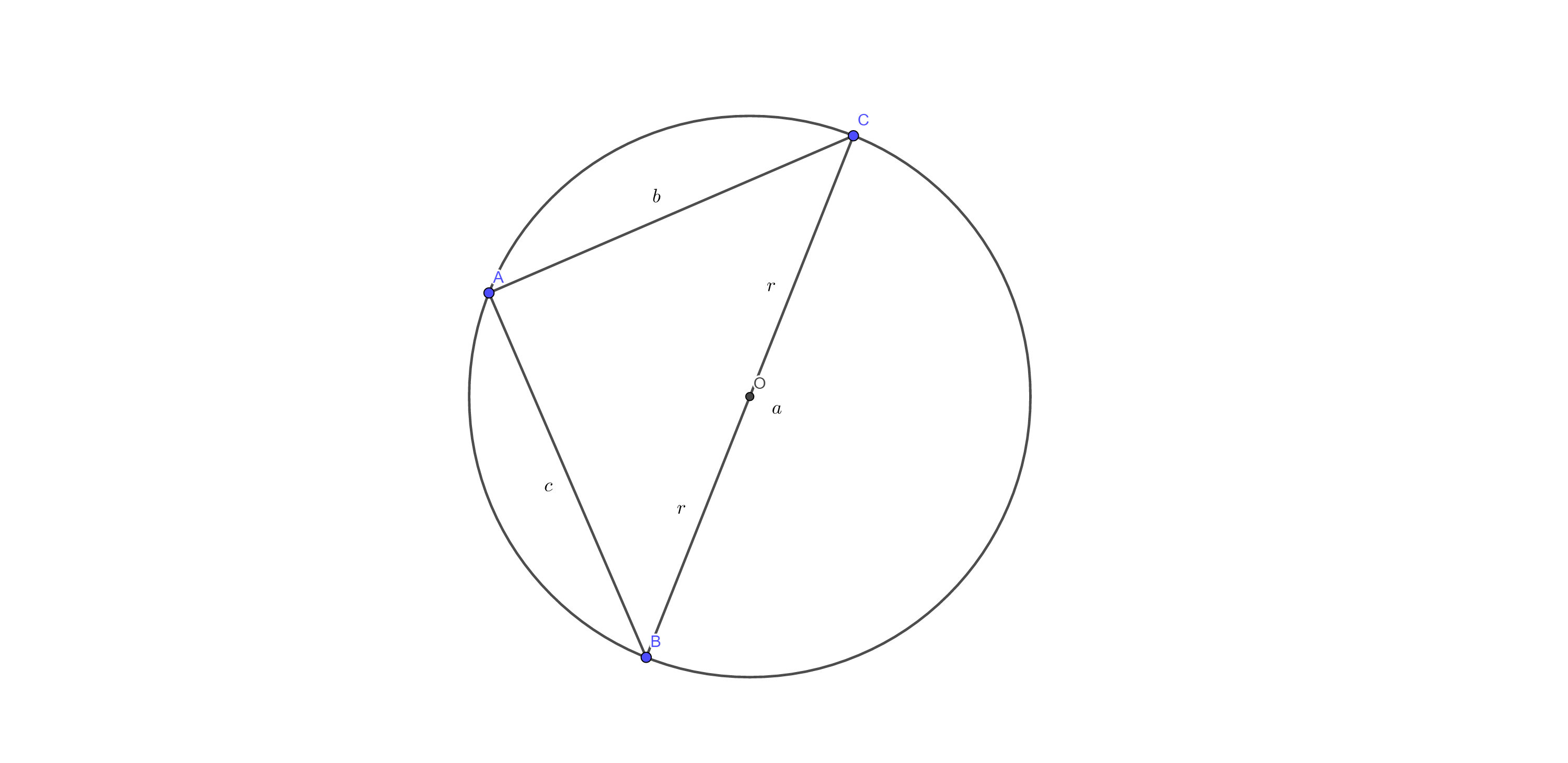
\[ \begin{align} \because \ & BC = a = 2r, \sin A = \sin \dfrac{\pi}{2} = 1 \\ \therefore \ & \dfrac{a}{\sin A} = 2r \end{align} \]

  • \(\angle A\)为钝角时

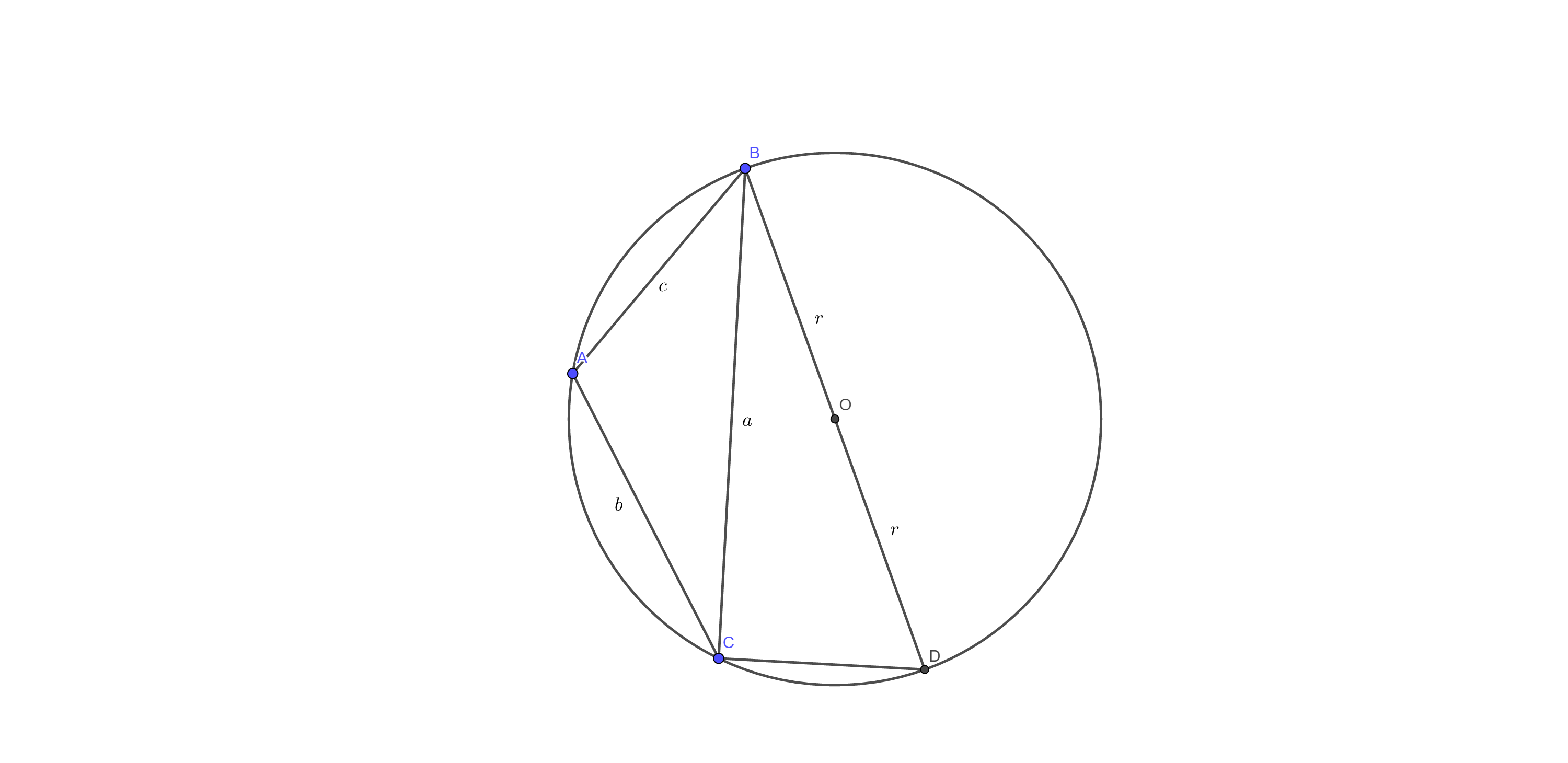
由于\(A, B, D, C\)四点共圆，所以\(\angle D + \angle A = 180^{\circ}\)。 \[ \begin{align} \therefore \ & \sin A = \sin D = \dfrac{a}{2r} \\ \therefore \ & \dfrac{a}{\sin A} = 2r \quad \Box \end{align} \]

余弦定理

如图，在\(\triangle ABC\)中，\(BC = a, AC = b, AB = c, \angle A = \alpha, \angle B = \beta, \angle C = \gamma\)。
余弦定理： \[c^{2} = a^{2} + b^{2} - 2ab \cos \gamma\] 同理： \[b^{2} = c^{2} + a^{2} - 2ca \cos \beta\] \[a^{2} = b^{2} + c^{2} - 2bc \cos \alpha\]

证明如下：

如图，过点\(C\)作\(CD \perp AB\)交\(AB\)于点\(D\)，\(CD = h\)。设\(AD = x\)，则\(BD = c - x\)。

根据勾股定理： \[ \begin{align} & b^{2} - x^{2} = h ^ {2} = a^{2} - (c - x)^{2} \\ \Rightarrow \ & b^{2} - x^{2} = a^{2} - c^{2} - x^{2} + 2cx \\ \Rightarrow \ & b^{2} = a^{2} - c^{2} + 2cx \\ \Rightarrow \ & x = \dfrac{b^{2} + c^{2} - a^{2}}{2c} \\ \Rightarrow \ & \cos \alpha = \dfrac{x}{b} = \dfrac{b^{2} + c^{2} - a^{2}}{2bc} \quad \Box \end{align} \]

射影定理

如图，在\(\triangle ABC\)中，\(BC = a, AC = b, AB = c, \angle A = \alpha, \angle B = \beta, \angle C = \gamma\)。
射影定理： \[a = b \cos \gamma + c \cos \beta\] 同理： \[b = c \cos \alpha + a \cos \gamma\] \[c = a \cos \beta + b \cos \alpha\]

证明如下：

如图，过点\(C\)作\(CD \perp AB\)交\(AB\)于点\(D\)。则\(AD = b \cos \alpha, BD = a \cos \beta\)。 \[c = AD + BD = b \cos \alpha + a \cos \beta \quad \Box\]

面积（海伦公式）

已知三角形三边边长分别为\(a, b, c\)，那么该三角形的面积\(S\)可以表示为：
\[S = \sqrt{s (s - a) (s - b) (s - c)}, s = \dfrac{a + b + c}{2}\]

证明如下：

如图，过点\(C\)作\(CD \perp AB\)交\(AB\)于点\(D\)，\(CD = h\)。设\(AD = x\)，则\(BD = c - x\)。

根据勾股定理： \[ \begin{align} & b^{2} = h^{2} + x^{2}, a^{2} = h^{2} + (c - x)^{2} \\ \Rightarrow \ & a^{2} - b^{2} = c^{2} - 2cd \\ \Rightarrow \ & x = - \dfrac{a^{2} - b^{2} - c^{2}}{2c} \end{align} \] \[ \begin{align} h^{2} &= b^{2} - x^{2} \\ &= b^{2} - (- \dfrac{a^{2} - b^{2} - c^{2}}{2c})^{2} \\ &= \dfrac{(2bc + a^{2} - b^{2} - c^{2}) (2bc - a^{2} + b^{2} + c^{2})}{4c^{2}} \\ &= \dfrac{(a^{2} - (b - c)^{2}) ((b + c)^{2} - a^{2})}{4c^{2}} \\ &= \dfrac{(a + b - c) (a - b + c) (b + c - a) (b + c + a)}{4c^{2}} \\ &= \dfrac{2(s - c) \cdot 2(s - b) \cdot 2(s - a) \cdot 2s}{4c^{2}} \\ &= \dfrac{4s (s - a) (s - b) (s - c)}{c^{2}} \\ S &= \dfrac{c \cdot h}{2} \\ &= \sqrt{\dfrac{c^{2}}{4} \cdot \dfrac{4s (s - a) (s - b) (s - c)}{c^{2}}} \\ & = \sqrt{s (s - a) (s - b) (s - c)} \quad \Box \end{align} \]

高线

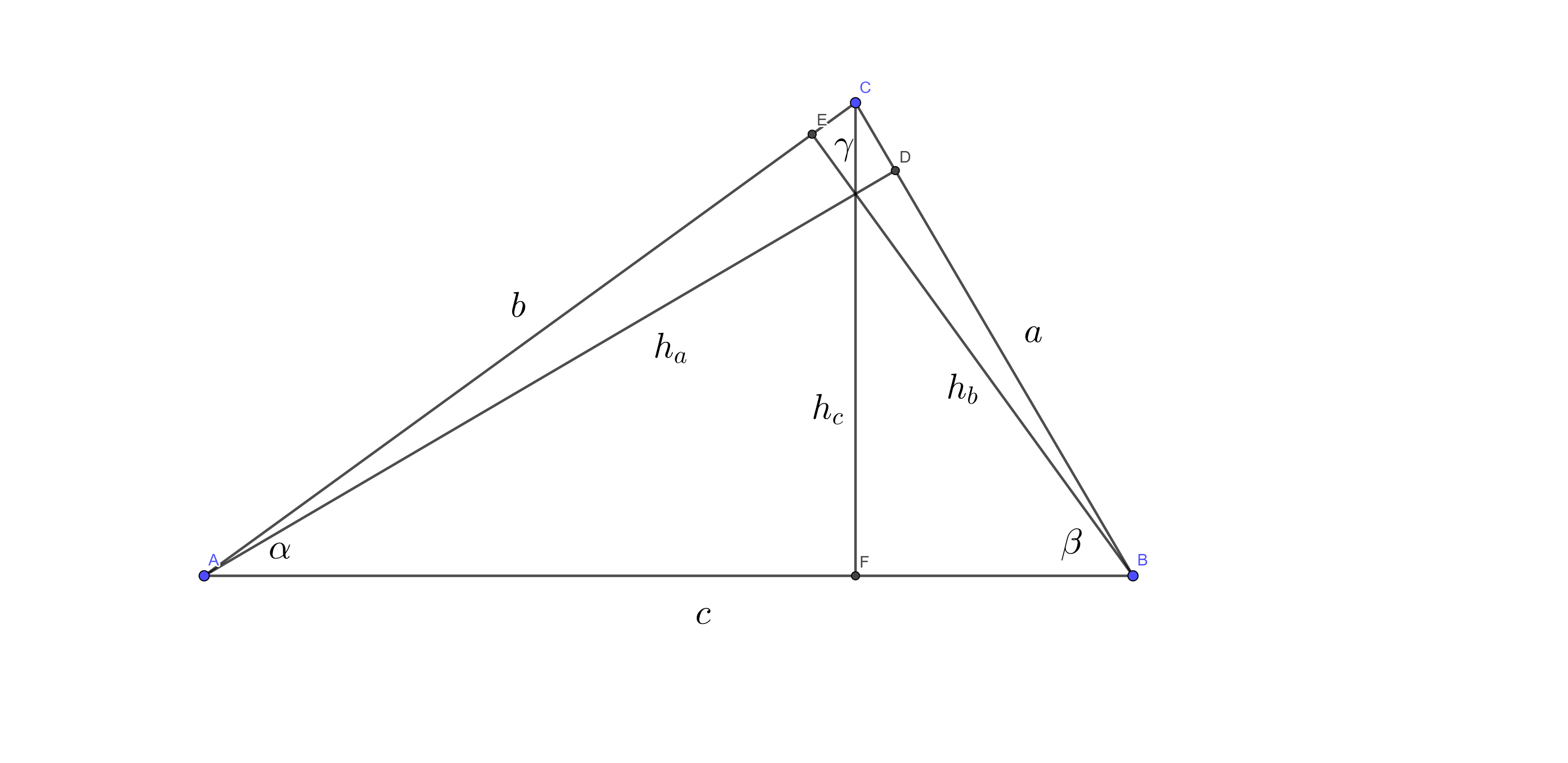
根据海伦公式，可以推出以三角形三边\(a, b, c\)为底的高线\(h_{a}, h_{b}, h_{c}\)长度： \[h_{a} = \dfrac{2 \sqrt{s (s - a) (s - b) (s - c)}}{a}\] \[h_{b} = \dfrac{2 \sqrt{s (s - a) (s - b) (s - c)}}{b}\] \[h_{c} = \dfrac{2 \sqrt{s (s - a) (s - b) (s - c)}}{c}\]

中线

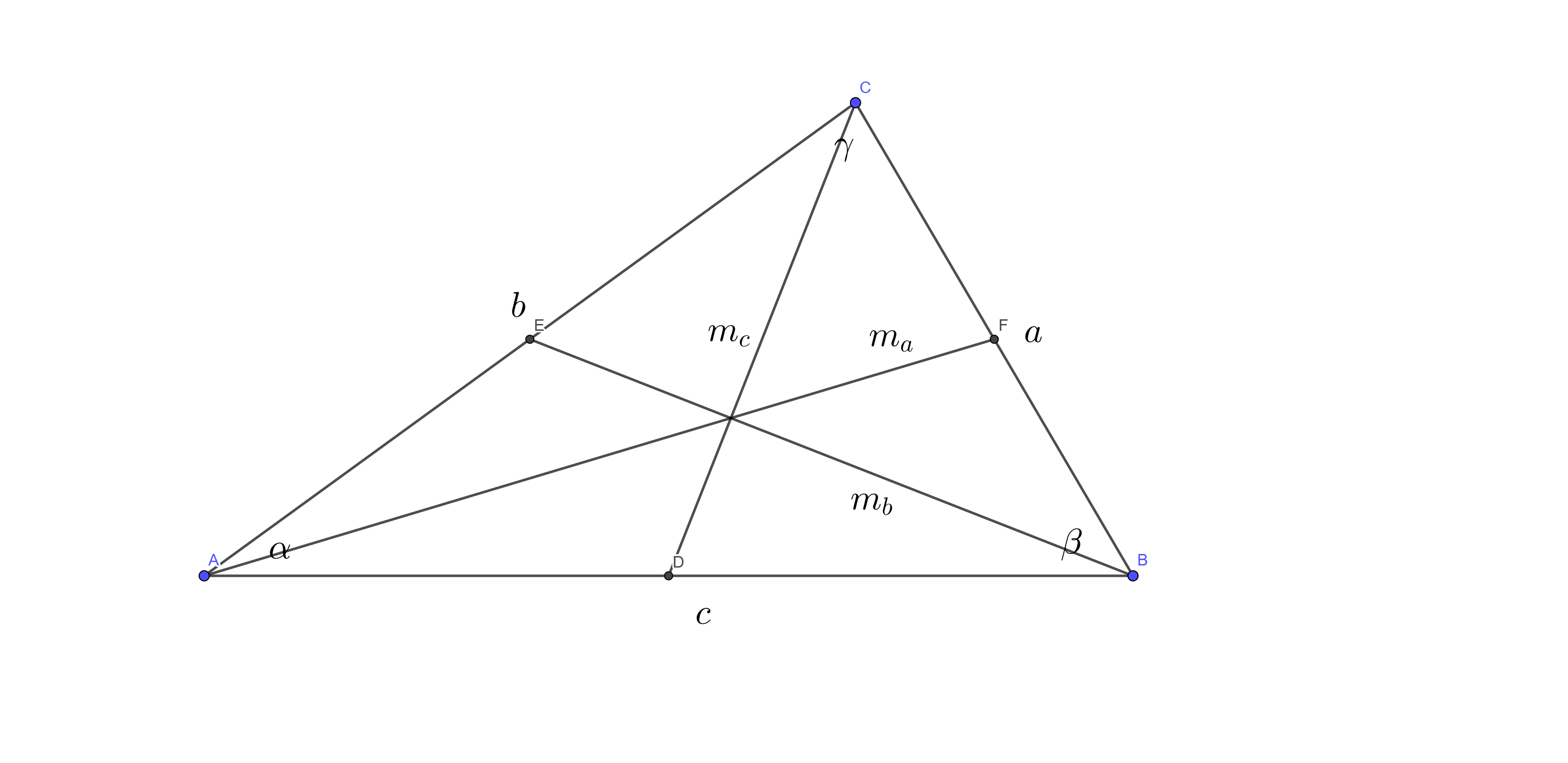
平分三角形三边\(a, b, c\)的中线\(m_{a}, m_{b}, m_{c}\)可以用以下公式计算长度： \[m_{a} = \dfrac{\sqrt{2(b^{2} + c^{2}) - a^{2}}}{2}\] \[m_{b} = \dfrac{\sqrt{2(c^{2} + a^{2}) - b^{2}}}{2}\] \[m_{c} = \dfrac{\sqrt{2(a^{2} + b^{2}) - c^{2}}}{2}\]

证明如下：

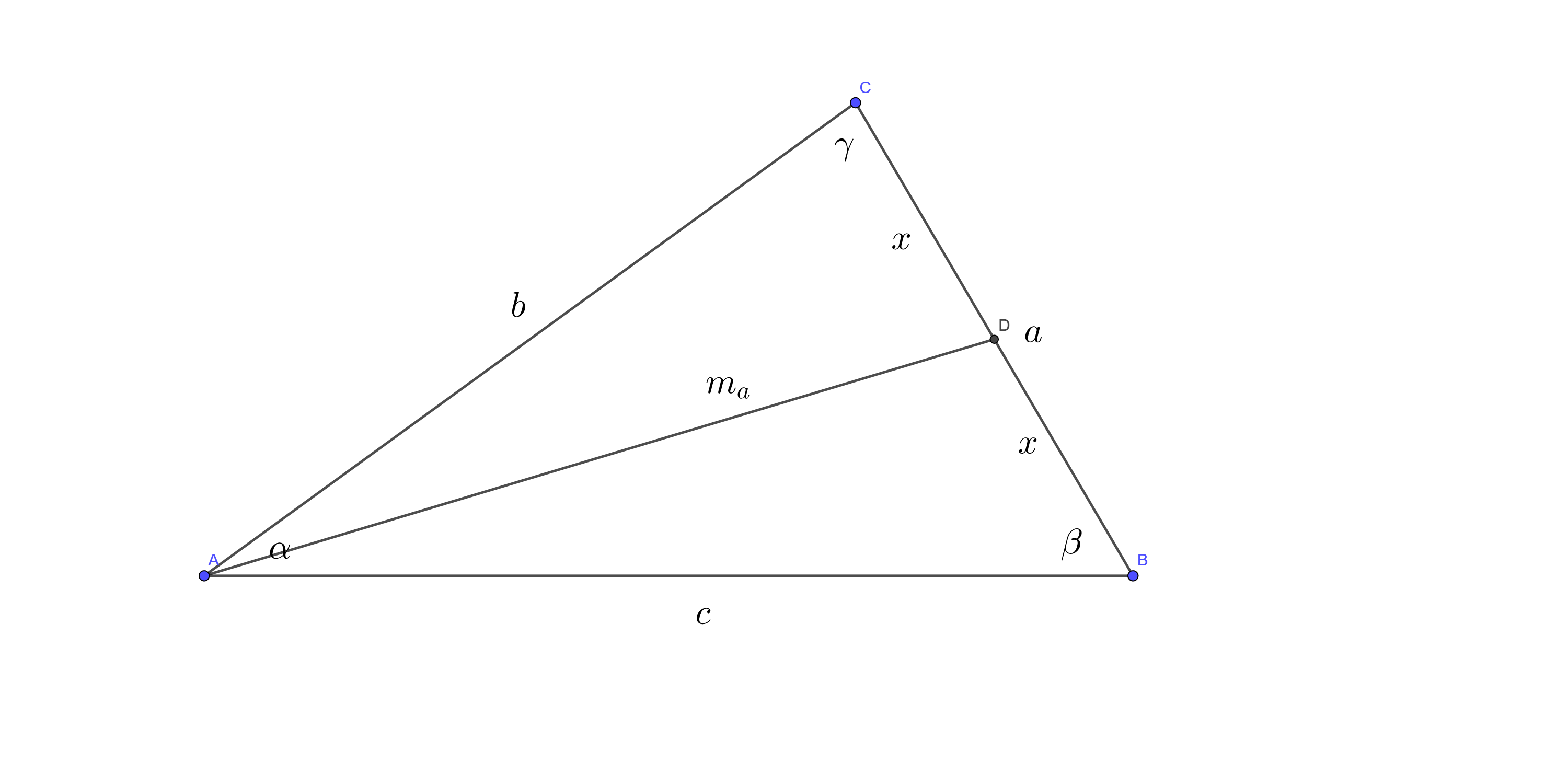如图，\(BC\)边上的中线\(AD = m_{a}\)。设\(BD = CD = x\)。

根据余弦定理： \[ \begin{align} m_{a}^{2} &= c^{2} + x^{2} - 2cx \cos \beta \\ &= c^{2} + (\dfrac{a}{2})^{2} - 2c \cdot \dfrac{a}{2} \cdot \dfrac{c^{2} + a^{2} - b^{2}}{2ca} \\ &= c^{2} + \dfrac{a^{2}}{4} - \dfrac{c^{2} + a^{2} - b^{2}}{2} \\ &= \dfrac{2b^{2} + 2c^{2} - a^{2}}{4} \\ \Rightarrow m_{a} &= \dfrac{\sqrt{2(b^{2} + c^{2}) - a^{2}}}{2} \quad \Box \end{align} \]

角平分线

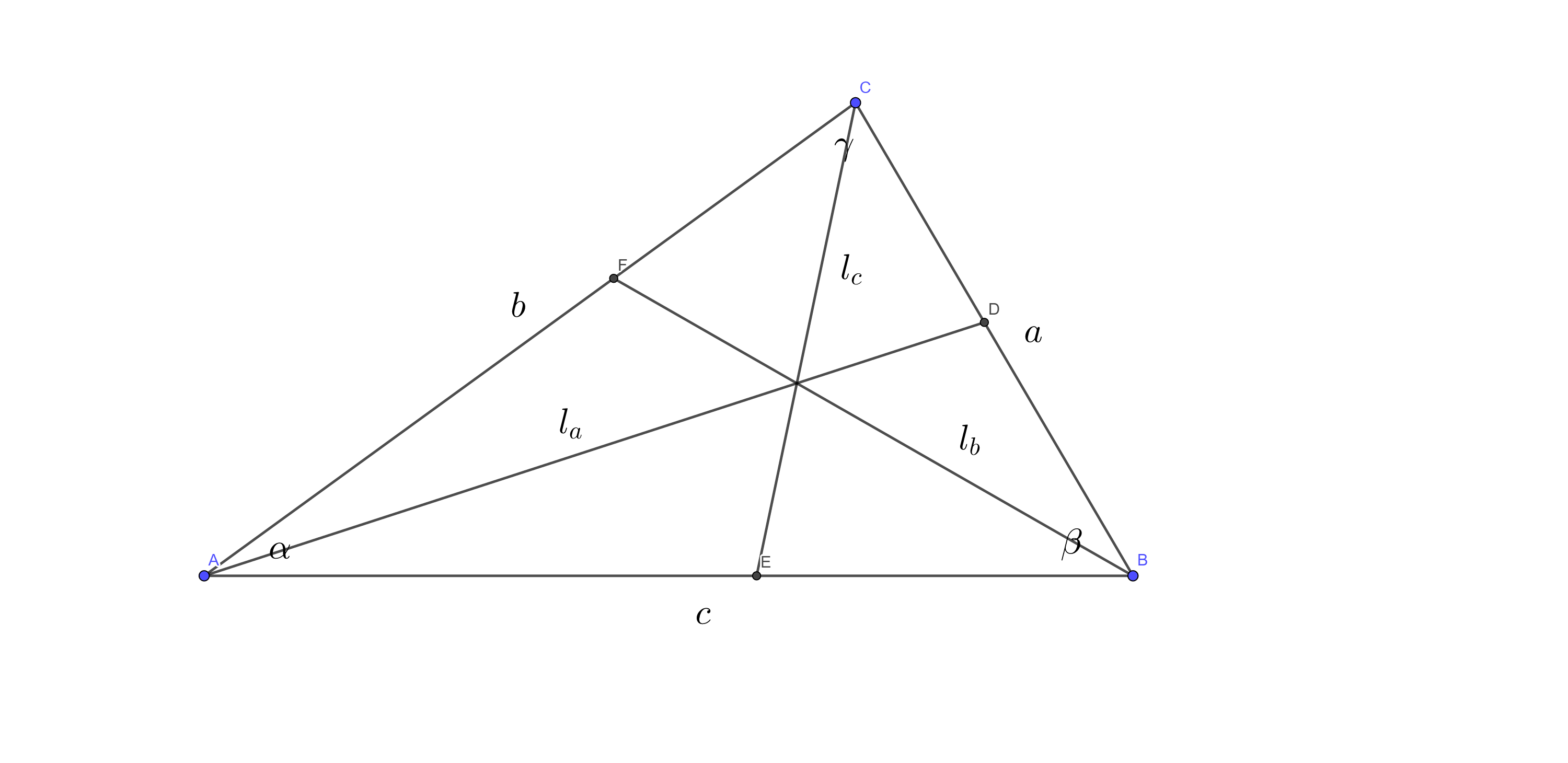
平分三角形三角\(\angle A, \angle B, \angle C\)的角平分线\(l_{a}, l_{b}, l_{c}\)可以用以下公式计算长度： \[l_{a} = \dfrac{\sqrt{bc (b + c + a) (b + c - a)}}{b + c}\] \[l_{b} = \dfrac{\sqrt{ca (c + a + b) (c + a - b)}}{c + a}\] \[l_{c} = \dfrac{\sqrt{ab (a + b + c) (a + b - c)}}{a + b}\]

证明如下：

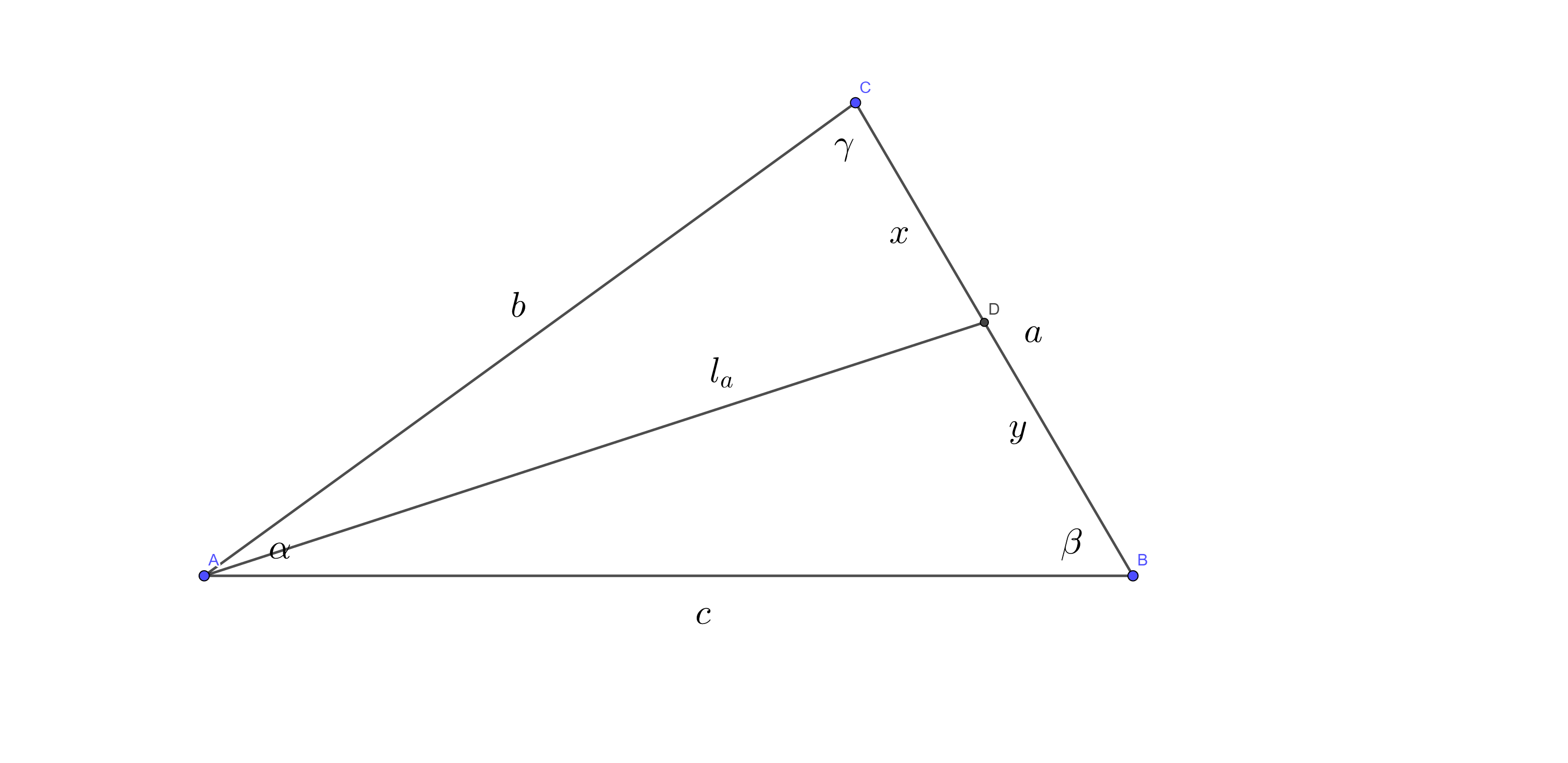如图，\(AD\)平分\(\angle A\)，\(AD = l_{a}\)。设\(CD = x, BD = y\)。

\[ \begin{align} \because \ & \angle CDA + \angle BDA = 180^{\circ} \\ \therefore \ & \sin \angle CDA = \sin \angle BDA \end{align} \] 根据正弦定理，\(\dfrac{\sin \angle CAD}{x} = \dfrac{\sin \angle CDA}{b}\)，即\(\dfrac{\sin \angle CAD}{\sin \angle CDA} = \dfrac{x}{b}\)。同理，\(\dfrac{\sin \angle BAD}{\sin \angle BDA} = \dfrac{y}{c}\)。 \[ \begin{align} \because \ & \sin \angle CDA = \sin \angle BDA, \sin \angle CAD = \sin \angle BAD \\ \therefore \ & \dfrac{x}{b} = \dfrac{y}{c} \\ \because \ & \begin{cases} x + y = a \\ \dfrac{x}{b} = \dfrac{y}{c} \end{cases} \\ \therefore \ & y = \dfrac{ac}{b + c} \end{align} \] 根据余弦定理： \[ \begin{align} l_{a}^{2} &= c^{2} + y^{2} - 2cy \cos \beta \\ &= c^{2} + (\dfrac{ac}{b + c})^{2} - 2c \cdot \dfrac{ac}{b + c} \cdot \dfrac{c^{2} + a^{2} - b^{2}}{2ca} \\ &= c^{2} + \dfrac{a^{2} c^{2}}{(b + c)^{2}} - \dfrac{c (c^{2} + a^{2} - b^{2})}{b + c} \\ &= \dfrac{bc (b^{2} + 2bc + c^{2} - a^{2})}{(b + c)^{2}} \\ &= \dfrac{bc (b + c + a) (b + c - a)}{(b + c)^{2}} \\ \Rightarrow l_{a} &= \dfrac{\sqrt{bc (b + c + a) (b + c - a)}}{b + c} \quad \Box \end{align} \]