简介

RMQ（range minimum/maximum query），即区间最值查询。
解决RMQ问题主要有两种方法：ST表（sparse table）和线段树（segment tree），本文主要讲ST表。

ST表适合解决静态区间最值查询，即下面的问题：

给定$n$个数，进行$m$次询问。对于每次询问，你都需要回答区间$[l, r]$中的最小值或最大值。

如果暴力做法，每次对区间$[x, y]$扫描一遍，肯定是过不了的，所以我们需要引入ST表。
ST表可以实现$O(n \log n)$的预处理和$O(1)$的查询。

代码

ST表基于倍增思想，由于$\min$操作允许区间重叠，也就是$\min(a, b, c) = \min(\min(a, b), \min(b, c))$（$\max$同理），因此我们可以通过两个有重叠的小区间来推出大区间。

令$f_{i, j}$表示$[i, i + 2^{j} - 1]$的最小值，
那么通过定义可得$f_{i, 0} = a_{i}$，
状态转移方程：$f_{i, j} = \min(f_{i, j - 1}, f_{i + 2^{j - 1}, j - 1})$。

E.G.

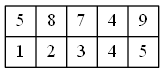
例如上面这个数组，当$i = 1, j = 2$时，$f_{i, j}$表示的是下标$1 - 4$的最小值$4$,
而$\min(f_{i, j - 1}, f_{i + 2^{j - 1}, j - 1})$表示的是取数组下标$1 - 2$和$3 - 4$中最小值的最小值，即$5, 4$的最小值，所以：
$f_{i, j} = \min(f_{i, j - 1}, f_{i + 2^{j - 1}, j - 1}) = \min(f_{1, 1}, f_{1 + 2, 1}) = \min(5, 4) = 4$。

以下是预处理代码：

int f[MAXN][LOGN];
void init() {
    for (int j = 1; j <= logn; ++j)
        for (int i = 1; i + (1 << j) - 1 <= n; ++i)
            f[i][j] = min(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
}

那么查询呢？

对于每个询问$[l, r]$，记区间长度为$len = r - l + 1$，我们从$l$往右找一段长为$2^{\log_{2} len}$的区间，$r$也往左找一段长为$2^{\log_{2} len}$的区间，也就是$[l, \log_{2} len], [r - 2^{\log_{2} len} + 1, \log_{2} len]$，显然这两个区间是覆盖整个区间的，所以取最小值即可。

int query(int l, int r) {
    int len = log(r - l + 1);
    return min(f[l][len], f[r - (1 << len) + 1][len]);
}

但是每次使用std::log2()函数计算$len$会降低效率，因此建议进行如下预处理：

$logn_{i} = \begin{cases} 0, & i = 1 \\ logn_{\frac{i}{2}} + 1, & i > 1 \end{cases}$

完整代码：

int f[MAXN][LOGN], lg[MAXN];
void init() {
    for (int j = 1; j <= logn; ++j)
        for (int i = 1; i + (1 << j) - 1 <= n; ++i)
            f[i][j] = min(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
    lg[1] = 0;
    for (int i = 2; i <= n; ++i)
        lg[i] = lg[i / 2] + 1;
}
int query(int l, int r) {
    int len = lg[r - l + 1];
    return min(f[l][len], f[r - (1 << len) + 1][len]);
}

求最大值同理，只要把min全部换成max就好了：

int f[MAXN][LOGN], lg[MAXN];
void init() {
    for (int j = 1; j <= logn; ++j)
        for (int i = 1; i + (1 << j) - 1 <= n; ++i)
            f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
    lg[1] = 0;
    for (int i = 2; i <= n; ++i)
        lg[i] = lg[i / 2] + 1;
}
int query(int l, int r) {
    int len = lg[r - l + 1];
    return max(f[l][len], f[r - (1 << len) + 1][len]);
}

简介

代码

例题