拓扑排序

发表于 分类于 阅读次数： Disqus： 本文字数： 689 阅读时长 ≈ 3 分钟

咕了这么久终于更新了

简介

拓扑排序（topological sort），是图论中的一种算法，简单点说就是：
对一个有向无环图（DAG）的节点进行线性排序，使得从点\(u\)到点\(v\)的每个有向边\(uv\)，\(u\)都在\(v\)之前。
当且仅当图没有环，即有向无环图时，该图存在拓扑排序。因此，拓扑排序可以用于判断图是否存在环。

拓扑排序可以形象地解释为：在某校中，每门课可能有若干门先修课，如果要修读某一门课，必须要先修读此课程所要求的所有先修课。假设一个学生同时只能修读一门课程，那么，他修完所有课程的顺序是一个拓扑序。

举个栗子：
对于下图，拓扑排序的结果是\(1 - 6 - 3 - 4 - 2 - 5\)。 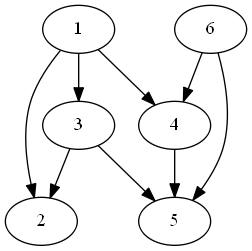E.G. 当然，拓扑排序的结果肯定是不唯一的，比如图片中\(6 - 1 - 4 - 3 - 5 - 2\)的顺序显然也可以。

代码

拓扑排序有多种算法，较为常用的有Kahn算法和DFS算法。

下文主要讲Kahn算法：
假设\(L\)是存放结果的集合，我们先把所有入度为\(0\)的节点找出来，放进\(L\)里。然后删除所有与该节点相连的边，再次寻找入度为\(0\)的点。重复上述步骤，直到找不到入度为\(0\)的点为止。若此时\(L\)的元素个数与节点总数相同，则排序完成；若不同，则说明原图存在环，无法排序。

代码很好实现： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// vector数组用来存边
std::vector<int> g[MAX_SIZE];
// in数组存每个点的入度
int in[MAX_SIZE];

// 计算入度
for (int i = 1; i <= size; ++i)
    for (int j = 0; j < int(g[i].size()); ++j)
        ++in[g[i][j]];

// 拓扑排序
bool toposort() {
    // 队列q存入度为0的点
    std::queue<int> q;
    // num存结果
    std::vector<int> num;
    // 所有入度为0的点入队
    for (int i = 1; i <= size; ++i)
        if (in[i] == 0)
            q.push(i);

    while (!q.empty()) {
        // 遍历与u相连的每条边
        int u = q.front();
        q.pop();
        num.push_back(u);
        for (int i = 0; i < int(g[u].size()); ++i) {
            // 终点v入度-1
            int v = g[u][i];
            --in[v];
            // 若v入度变成了0就入队
            if (in[v] == 0)
                q.push(v);
        }
    }

    // 有拓扑序列就输出
    if (int(num.size()) == size) {
        for (int i = 0; i < size; ++i)
            printf("%d ", num[i]);
        return true;
    }
    return false;
}

假设这个图\(G = (V, E)\)初始化in数组的时候需要遍历整张图，因此有\(O(V + E)\)的复杂度。然后对其进行操作，显然也是需要\(O(V + E)\)的时间复杂度。所以该算法总的时间复杂度为\(O(V + E)\)。

例题