堆
简介
堆（heap）是一种树型数据结构，具有以下特点：
- 堆中某个节点的值总是不大于或不小于其父节点的值
- 堆总是一棵完全二叉树
根节点最大的堆称为大根堆，相反则称之为小根堆。
堆可以用于排序。
例如图中就是一个大根堆：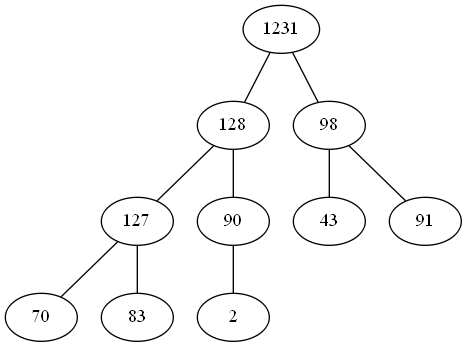 
代码
大根堆较小根堆更容易实现。以下，我们用C++来实现大根堆模板。
我们用class来封装堆的模板类： 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19const int MAX_SIZE = 100000;
class Heap {
private:
int ele[MAX_SIZE];
int tot;
int le(int n);
int rt(int n);
int dad(int n);
public:
Heap();
bool push(int e);
bool pop();
bool empty();
int top();
int size();
};MAX_SIZE为100000，然后用数组ele来存储元素。tot用于存储当前元素数量，同时也是最后一个元素的位置。
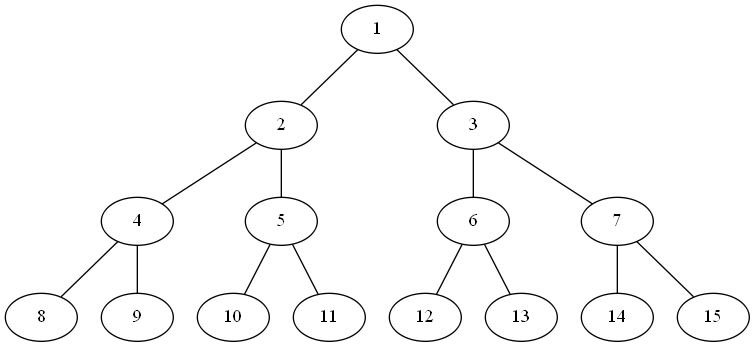我们给每个节点编号，可以发现编号为\(n\)的节点的左子节点为\(2n\)、右子节点为\(2n + 1\)、父节点为\(\lfloor \dfrac{n}{2}
\rfloor\)。因此，我们用三个私有方法le(int n)、rt(int n)、dad(int n)分别表示n号元素的左子节点、右子节点、父节点的位置：
1
2
3
4
5
6
7
8
9int Heap::le(int n) {
return n << 1;
}
int Heap::rt(int n) {
return (n << 1) + 1;
}
int Heap::dad(int n) {
return n >> 2;
}
构造函数Heap()用于初始化： 1
2
3Heap::Heap() {
tot = 0;
}
我的堆模板中有5个公有方法：
push(int e)：把元素e压入堆，成功返回truepop()：弹出根节点元素，成功返回trueempty()：若堆为空返回truetop()：返回根节点元素size()：返回节点数
我们看这张图，如果要把\(20\)压入堆，要如何实现呢？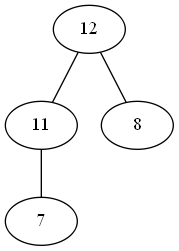 
首先，在尾部添加一个元素\(20\)： 
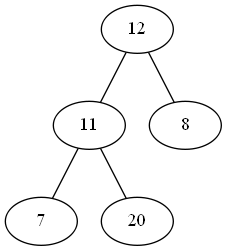然后，我们将它与父节点\(11\)比较，发现\(20 >
11\)，不符合大根堆的性质。于是我们将其与父节点交换：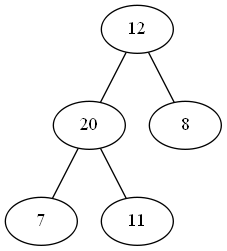 
交换后，\(20\)仍然大于其父节点，也就是根节点\(12\)。因此，我们可以再进行一次交换： 
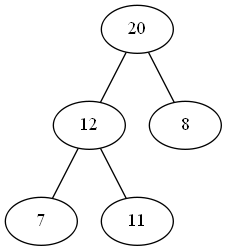这样就完成了把\(20\)压入堆的操作。
由此可见，每次插入操作都需要对堆进行调整，时间复杂度为\(O(\log n)\)。
代码实现： 1
2
3
4
5
6
7
8
9
10
11
12
13bool Heap::push(int e) {
if (tot == MAX_SIZE - 1)
return false;
ele[++tot] = e;
for (int i = tot; i != 1; i = dad(i)) {
if (ele[i] > ele[dad(i)])
std::swap(ele[i], ele[dad(i)]);
else
break;
}
return true;
}tot == MAX_SIZE - 1，这是为了防止溢出。
如果要删除根节点呢？ 还是刚才那张图，我们可以先把根节点\(20\)与最后一个节点\(11\)交换，然后删除这个节点：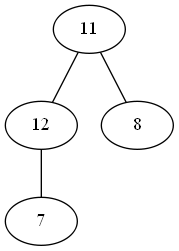 
由于根节点最大的性质，我们必须要让一个最大的数来代替\(11\)成为根节点。\(11\)的2个子节点中，只有\(12\)满足条件，因此要交换\(11\)和\(12\)： 就完成了删除操作。
同样，删除操作的时间复杂度也是\(O(\log
n)\)，代码如下： 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18bool Heap::pop() {
if (empty()) {
return false;
}
std::swap(ele[1], ele[tot]);
ele[tot--] = 0;
for (int i = 1; ; ) {
int tar = (ele[le(i)] > ele[rt(i)] ? le(i) : rt(i));
if (ele[i] < ele[tar]) {
std::swap(ele[i], ele[tar]);
i = tar;
}
else
break;
}
return true;
}
剩下3个方法就很好理解了： 1
2
3
4
5
6
7
8
9
10
11bool Heap::empty() {
return tot == 0;
}
int Heap::top() {
return ele[1];
}
int Heap::size() {
return tot;
}
这样基本上就实现了堆的所有功能，完整代码： 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77const int MAX_SIZE = 100000;
class Heap {
private:
int ele[MAX_SIZE];
int tot;
int le(int n);
int rt(int n);
int dad(int n);
public:
Heap();
bool push(int e);
bool pop();
bool empty();
int top();
int size();
};
int Heap::le(int n) {
return n << 1;
}
int Heap::rt(int n) {
return (n << 1) + 1;
}
int Heap::dad(int n) {
return n >> 2;
}
Heap::Heap() {
tot = 0;
}
bool Heap::push(int e) {
if (tot == MAX_SIZE - 1)
return false;
ele[++tot] = e;
for (int i = tot; i != 1; i = dad(i)) {
if (ele[i] > ele[dad(i)])
std::swap(ele[i], ele[dad(i)]);
else
break;
}
return true;
}
bool Heap::pop() {
if (empty())
return false;
std::swap(ele[1], ele[tot]);
ele[tot--] = 0;
for (int i = 1; ; ) {
int tar = (ele[le(i)] > ele[rt(i)] ? le(i) : rt(i));
if (ele[i] < ele[tar]) {
std::swap(ele[i], ele[tar]);
i = tar;
}
else
break;
}
return true;
}
bool Heap::empty() {
return tot == 0;
}
int Heap::top() {
return ele[1];
}
int Heap::size() {
return tot;
}
此外，我们可以用template实现真正的模板类： 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87const int MAX_SIZE = 100000;
template<class type>
class Heap {
private:
type ele[MAX_SIZE];
int tot;
int le(int n);
int rt(int n);
int dad(int n);
public:
Heap();
bool push(type e);
bool pop();
bool empty();
type top();
int size();
};
template<class type>
int Heap<type>::le(int n) {
return n << 1;
}
template<class type>
int Heap<type>::rt(int n) {
return (n << 1) + 1;
}
template<class type>
int Heap<type>::dad(int n) {
return n >> 1;
}
template<class type>
Heap<type>::Heap() {
tot = 0;
}
template<class type>
bool Heap<type>::push(type e) {
if (tot == MAX_SIZE - 1)
return false;
ele[++tot] = e;
for (int i = tot; i != 1; i = dad(i)) {
if (ele[i] > ele[dad(i)])
std::swap(ele[i], ele[dad(i)]);
else
break;
}
return true;
}
template<class type>
bool Heap<type>::pop() {
if (empty())
return false;
std::swap(ele[1], ele[tot]);
ele[tot--] = 0;
for (int i = 1; ; ) {
int tar = (ele[le(i)] > ele[rt(i)] ? le(i) : rt(i));
if (ele[i] < ele[tar]) {
std::swap(ele[i], ele[tar]);
i = tar;
}
else
break;
}
return true;
}
template<class type>
bool Heap<type>::empty() {
return tot == 0;
}
template<class type>
type Heap<type>::top() {
return ele[1];
}
template<class type>
int Heap<type>::size() {
return tot;
}Heap<type>的方式调用即可，例如声明一个long long类型的大根堆hp：Heap<long long> hp。
堆排序
利用堆的子节点总比父节点小或大的性质，就可以进行\(O(n \log n)\)的排序。
实现过程很简单，只要将待排序数列一个一个压入堆，然后一个一个输出根节点并弹出即可。
大根堆可以从大到小排序，小根堆可以从小到大排序。
用上面的大根堆模板对数组进行从大到小的排序： 1
2
3
4
5
6
7
8
9
10
11template<class type>
void HeapSort(type num[], int len) {
Heap<type> hp;
for (int i = 0; i < len; ++i)
hp.push(num[i]);
for (int i = 0; i < len; ++i) {
num[i] = hp.top();
hp.pop();
}
}
STL
STL提供了一种类似于堆的数据结构：优先队列（priority
queue）。
std::priority_queue包含在头文件<queue>中，共有3个参数：
1
2
3
4
5template<
class T,
class Container = std::vector<T>,
class Compare = std::less<typename Container::value_type>
> class priority_queue;
T：元素类型Container：用于存储元素的容器类型，元素类型必须与T一致，默认为std::vectorCompare：比较方式，默认为std::less即小于（实现大根堆），传入std::greater可以实现小根堆
例如，我们要定义一个double类型的小根堆pq，可以用：
1
std::priority_queue<double, std::vector<double>, std::greater<double>> pq;
>>写在一起会报错。若不支持C++
11标准，需要在中间加一个空格： 1
std::priority_queue<double, std::vector<double>, std::greater<double> > pq;
std::priority_queue同样有5个方法：
push()pop()empty()top()size()
这5个方法作用同上。